Круговой процесс. Обратимые и необратимые процессы

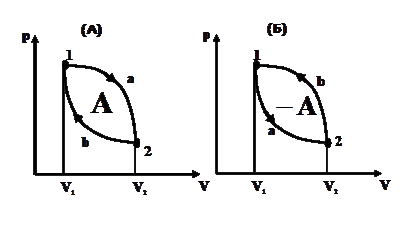
Круговым процессом (или циклом) называется процесс, при котором система, пройдя через ряд состояний, возвращается в исходное состояние. На (р,V)-диаграмме цикл изобража­ется замкнутой кривой, где участок 1-2 соответствует расширению, а 2-1 - сжатию газа (рис. 16).

Работа расширения А₁ (площадь фигуры 1a2V₂V₁1)- положительна: .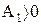

Работа сжатия A₂ (площадь фигуры 2b1V₁V₂2) - отрицательна: .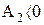

Работа за цикл А определяется площадью, охватываемой замкнутой кривой:

Рис. 16. Круговой процесс

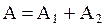
Таким образом, работа - это функция не только состояния термодинамической системы, но и вида процесса, который происходит.

Поэтому работа не является однозначной функцией состояния (такой, как внутренняя энергия). Из первого начала термодинамики следует, что теплота , так же как и работа , является функцией процесса, который происходит с системой.

Цикл называется прямым, если за цикл совершается положительная работа 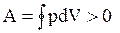(цикл протекает по часовой стрелке – рис. 16, А).

Цикл называется обратным, если за цикл совершается отрицательная работа 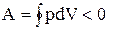(цикл протекает против часовой стрелки - рис. 16, В).

Прямой цикл используется в тепловых двигателях (совершают работу за счет полученной извне теплоты). Обратный цикл используется в холодильных машинах (за счет работы внешних сил теплота переносится к телу с более высокой температурой).

КПД кругового процесса: в результате кругового процесса система возвращается в исходное состояние, следовательно, полное изменение внутренней энергии равно нулю. Поэтому 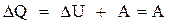, то есть работа, совершаемая за цикл, равна количеству полученной извне теплоты. Если в ходе кругового процесса система не только получает количество теплоты 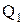, но и теряет (отдает) количество теплоты 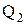, то .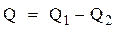

Термический коэффициент полезного действия для кругового процесса - это величина, равная отношению работы, совершенной системой, к количеству теплоты, полученному в этом цикле системой:

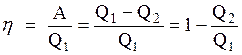
Термодинамический процесс называется обратимым, если он может происходить как в прямом, так и в обратном направлении. Причем, если такой процесс происходит сначала в прямом, а затем в обратном направлении и система возвращается в исходное состояние, то в окружающей среде и в этой системе не происходит никаких изменений. Всякий процесс, не удовлетворяющий этим условиям, является необратимым.

Реальные процессы необратимы, в них всегда происходит диссипация (потеря) энергии (из-за трения, теплопроводности и т.д.). Обратимые процессы - это физическая модель (идеализация реальных процессов).

Энтропия

Количество тепла 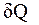, которое должно быть доставлено системе или отнято у неё при переходе от одного состояния в другое, не определяется однозначно начальным и конечным состояниями, но существенно зависит от способа осуществления этого перехода ( 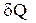не является функцией состояния системы).

Однако, приведенное количество теплоты - отношение теплоты 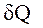к температуре 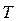системы при бесконечно малых изменениях состояния системы - есть функция состояния системы. В любом обратимом круговом процессе: 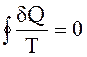. Следовательно, подинтегральное выражение есть полный дифференциал некоторой функции, которая определяется только начальным и конечным состояниями системы и не зависит от пути, каким система пришла в это состояние.

Энтропией 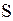называется функция состояния системы, дифференциалом которой является :

.

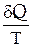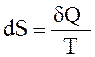Таким образом, первое начало термодинамики 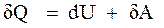можно записать в виде .

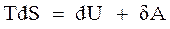В замкнутой системе для обратимых процессов 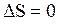; для необратимых циклов 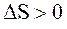. Последние два условия можно представить виде неравенства Клаузиуса: энтропия замкнутой системы может либо возрастать (в случае необратимых процессов) либо оставаться постоянной (в случае обратимых процессов):

.

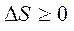Поскольку 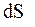и 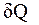имеют один и тот же знак, то по характеру изменения энтропии можно судить о направлении процесса теплообмена. При нагревании тела 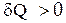и его энтропия возрастает 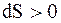, при охлаждении 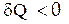и энтропия тела убывает .

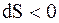Изоэнтропийным называется процесс, протекающий при постояннойэнтропии ( 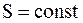). В обратимом адиабатном процессе 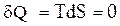, так что 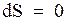и 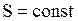, поэтому адиабатный процесс является изоэнтропийным.

Рассмотрим для примера идеальный газ, совершающий равновесный переход из состояния 1 в состояние 2. Изменение его энтропии

.

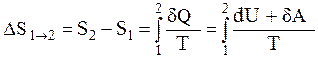Используя известные соотношения: 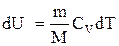; ; 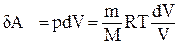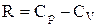и 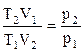, можно получить выражение 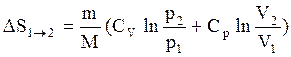, из которого видно, что изменение энтропии идеального газа при переходе его из состояния 1 в состояние 2 не зависит от вида процесса этого перехода.

Изменение энтропии в процессах идеального газа

Изохорный ( 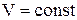)	Изобарический ( 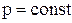)	Изотермический ( 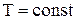)	Адиабатический ( 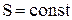)
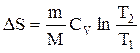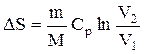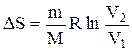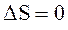