Молекулярная физика и термодинамика

Молекулярная физика и термодинамика

Учебное пособие

Ростов-на-Дону 2010

УДК 530

К 91

К 91 А.Б. Гордеева, Т.П. Жданова, Н.В. Пруцакова, А.Я. Шполянский Молекулярная физика и термодинамика: Учеб. пособие. – Ростов н/Д: Издательский центр ДГТУ, 2010. – с.

Учебное пособие содержит описание основных явлений и законов молекулярной физики и термодинамики, основные положения молекулярно-кинетической теории, модели идеального и реального газов, газовые законы, первое и второе начала термодинамики, понятие энтропии, свойства жидкостей.

Цель пособия – оказать помощь студентам первого и второго курсов технических и инженерно-экономических специальностей при освоении теоретического материала, решении задач, подготовке к выполнению лабораторных работ по разделу «Молекулярная физика и термодинамика». Предназначено для студентов очной, заочной и ускоренной форм обучения.

Печатается по решению редакционно-издательского совета

Донского государственного технического университета

Научный редактор канд. хим. наук, доц. А.Я. Шполянский

© А.Б. Гордеева, Т.П. Жданова, Н.В. Пруцакова,

А.Я. Шполянский, 2010

© Издательский центр ДГТУ, 2010

МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ ИДЕАЛЬНЫХ ГАЗОВ

Основные положения молекулярно-кинетической теории

Молекулярно-кинетическая теория (МКТ) основана настатистическом методе, поэтому иногда ее называют статистической физикой. МКТ изучает микроскопическую структуру макроскопических объектов. Основные положения МКТ:

1. Вещество имеет дискретную структуру – состоит из частиц (молекул и атомов), разделенных промежутками.

2. Частицы находятся в непрерывном хаотическом движении.

3. Частицы взаимодействуют друг с другом: на расстояниях, сравнимых с размерами молекул, преобладают силы отталкивания, на более дальних – силы притяжения. Эти силы взаимодействия имеют электромагнитную природу.

Задачей МКТ является не описание движения отдельных частиц, а определение макроскопических параметров системы - таких, как масса, объем, давление, температура и т.п.

Перечислим некоторые явления, подтверждающие правильность исходных идей МКТ: газ занимает любой предоставленный ему объем, значит, молекулы движутся независимо друг от друга; диффузия веществ ‑ подтверждает предположение о непрерывном хаотическом движении молекул; давление газов на стенки сосуда объясняется ударами молекул о стенки сосуда; броуновское движение – следствие того, что движущиеся молекулы бомбардируют инородные частицы.

Законы идеального газа

В молекулярно-кинетической теории используется модель идеального газа, в которой считают:

1) собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда;

2) между молекулами газа отсутствуют силы взаимодействия;

3) столкновения молекул газа между собой и со стенками сосуда абсолютно упругие.

Реальные газы при низких давлениях и высоких температурах близки по своим свойствам к идеальному газу.

Рассмотрим эмпирические законы, описывающие поведение идеальных газов.

1. Закон Бойля – Мариотта:для данной массы газа при постоянной температуре произведение давления газа на его объем есть величина постоянная:

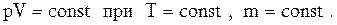
Процесс, протекающий при постоянной температуре, называется изотермическим. Кривая, изображающая зависимость между величинами , характеризующими свойства вещества при постоянной температуре, называется изотермой. Изотермы представляют собой гиперболы, расположенные тем выше, чем выше температура, при которой происходит процесс (рис. 1).

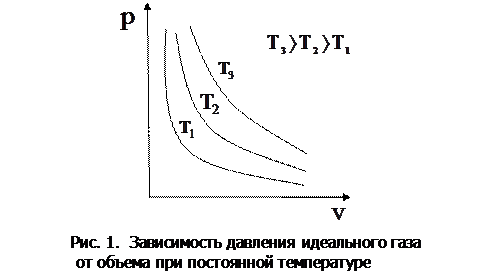
2. Закон Гей-Люссака: объем данной массы газа при постоянном давлении изменяется с температурой линейно:

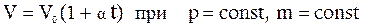. (1)

Здесь 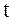- температура по шкале Цельсия, 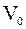- объем газа при 0 ⁰С,
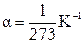- температурный коэффициент объемного расширения газа.

Процесс, протекающий при постоянном давлении и неизменной массе газа, называется изобарным. В ходе изобарного процесса для газа данной массы отношение объема к термодинамической температуре постоянно:

.

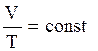На диаграмме в координатах 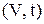этот процесс изображается прямой, называемой изобарой(рис. 2).

3. Закон Шарля: давление данной массы газа при постоянном объеме изменяется линейно с температурой:

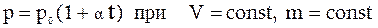. (2)

Здесь 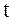- температура по шкале Цельсия, 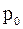- давление газа при 0 ⁰С, 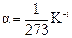- температурный коэффициент давления газа.

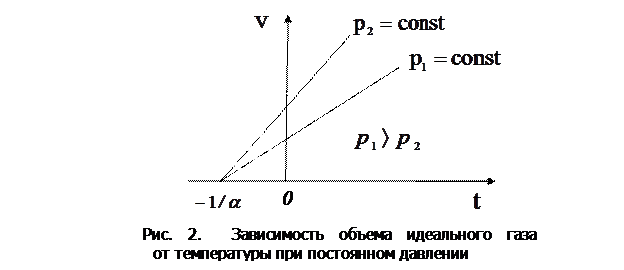
Процесс, протекающий при постоянном объеме и неизменной массе газа, называется изохорным. В ходе изохорного процесса для газа данной массы отношение давления к термодинамической температуре постоянно:

.

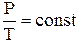На диаграмме в координатах 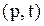этот процесс изображается прямой, называемой изохорой(рис. 3).

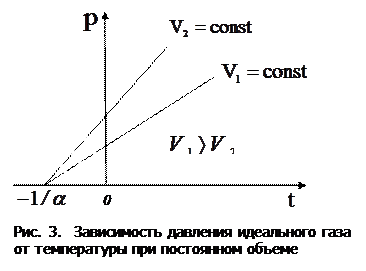
Вводя в формулах (1) и (2) термодинамическую температуру T, законам Гей-Люссака и Шарля можно придать более удобный вид: ,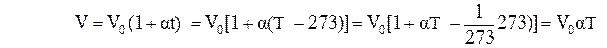

.

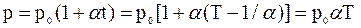Закон Авогадро: моли любых газов при одинаковых температуре и давлении занимают одинаковые объемы.

Так, при нормальных условиях один моль любого газа занимает объем 22,4 м^-3. При одинаковых температуре и давлении любой газ содержит в единице объема одинаковое количество молекул.

При нормальных условиях в 1 м³ любого газа содержится число частиц, называемое числом Лошмидта:

.

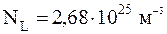Закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений 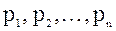входящих в нее газов:

.

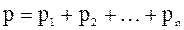Парциальное давление – давление, которое создавал бы газ, входящий в состав газовой смеси, если бы он занимал объем, равный объему смеси при той же температуре.

Распределение Больцмана

При выводе основного уравнения МКТ предполагалось, что на молекулы не действуют внешние силы, и поэтому молекулы равномерно распределены по объему. Но молекулы любого газа находятся в потенциальном поле тяготения Земли. Тяготение, с одной стороны, и тепловое движение молекул – с другой, приводят к некоторому стационарному состоянию газа, при котором концентрация молекул и давление газа убывают с высотой.

Если температура воздуха 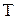и ускорение свободного падения 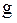не меняются с высотой, то давление воздуха 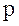на высоте 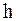, отсчитанной от некоторого уровня, принятого за начальный, связано с давлением 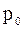на этом начальном уровне экспоненциальной зависимостью:

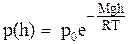. (16)

Выражение (16) называется барометрической формулой. Оно позволяет найти атмосферное давление в зависимости от высоты или, измерив давление, найти высоту. Из формулы (16) сле­дует, что давление убывает с высотой тем быстрее, чем тяжелее газ (чем больше его молярная масса 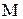) и чем ниже температура .

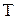Барометрическую формулу (16) можно преобразовать, воспользовавшись выражением (8):

,

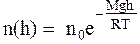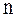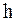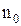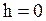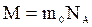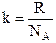Где – концентрация молекул на высоте , – концентрация молекул на высоте . Так как и , то

,

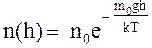где 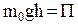- потенциальная энергия одной молекулы в поле тяготения, и

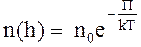. (17)

Выражение (17) называют распределением Больцмана для внешнего потенциального поля. Из него следует, что при постоянной температуре плотность газа больше там, где меньше потенциальная энергия его молекул.

Из формулы (17) следует, что с понижением температуры число частиц на высотах, отличных от нуля, убывает, обращаясь в нуль при 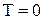. При абсолютном нуле все молекулы расположились бы на земной поверхности. При высоких температурах, напротив, 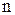слабо убывает с высотой, так что молекулы оказываются распределенными по высоте почти равномерно.

Этот факт имеет простое физическое объяснение. Каждое конкретное распределение молекул по высоте устанавливается в результате действия двух тенденций: 1) притяжение молекул к Земле (характеризуемое силой 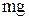) стремится расположить их на поверхности Земли; 2) тепловое движение (характеризуемое величиной 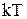) стремится разбросать молекулы равномерно по всем высотам. Чем больше 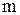и меньше 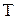, тем сильнее преобладает первая тенденция, и молекулы сгущаются у поверхности Земли. В пределе при 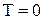тепловое движение совсем прекращается, и под влиянием силы притяжения молекулы располагаются на земной поверхности. При высоких температурах превалирует тепловое движение, и плотность молекул медленно убывает с высотой.

Явления переноса

Молекулы газа, находясь в состоянии хаотического движения, непрерывно сталкиваются друг с другом. Между двумя последовательными столкновениями молекулы проходят некоторый путь 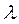, который называется длиной свободного пробега. В общем случае длина пути между последовательными столкновениями различна, но так как в движении участвует огромное число молекул и они находятся в беспорядочном движении, то можно говорить о средней длине свободного пробега молекул .

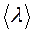Из основных положений МКТ получена формула для определения средней длины свободного пробега:

,

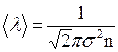где 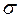- эффективный диаметр молекулы, 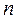- число молекул в единице объема газа.

При постоянной температуре 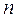пропорционально давлению, следовательно, средняя длина свободного пробега обратно пропорциональна давлению газа.

Эффективный диаметр молекулы - это минимальное расстояние, на которое сближаются при столкновении центры двух молекул. Эффективный диаметр больше истинного и зависит от энергии молекул, а, следовательно, и от температуры.

В термодинамически неравновесных системах возникают особые необратимые процессы, называемые явлениями переноса, в результате которых происходит пространственный перенос энергии, массы и импульса. К таким явлениям относятся теплопроводность (обусловлена переносом молекулами энергии), диффузия (обусловлена переносом молекулами массы) и внутреннее трение, или вязкость (обусловлено переносом молекулами импульса). Каждое из явлений переноса связано с неодинаковостью в пространстве значений некоторой величины (соответственно: температуры, концентрации и скорости).

Явление теплопроводности заключается в обмене энергиями между молекулами газа при их столкновении. В результате происходит процесс выравнивания средних кинетических энергий молекул, а, следовательно, температур. Перенос энергии в форме теплоты подчиняется закону Фурье:

,

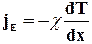где 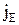- плотность теплового потока (количество энергии, переносимой в форме теплоты в единицу времени через единичную площадку, перпендикулярную оси х), 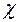- коэффициент теплопроводности, 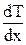- градиент температуры, показывающий, как быстро меняется температура газа от слоя к слою на единицу длины в направлении нормали к этой площадке. Знак минус показывает, что перенос энергии происходит в сторону убывания температуры. Коэффициент теплопроводности:

,

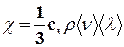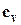- удельная теплоемкость газа при постоянном объеме, 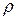- плотность газа, 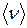- средняя скорость теплового движения молекул, 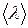- средняя длина свободного пробега молекул.

Диффузия – самопроизвольное проникновение и перемешивание частиц двух соприкасающихся газов, жидкостей и твердых тел. Для химически однородного газа диффузия подчиняется закону Фика:

,

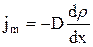где 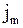- плотность потока массы (масса вещества, перемещающегося в единицу времени через единичную площадку, перпендикулярно оси х), 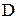- коэффициент диффузии, 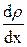- градиент плотности, равный скорости изменения плотности на единицу длины х в направлении нормали к этой площадке. Знак минус показывает, что перенос массы происходит в направлении убывания плотности. Коэффициент диффузии:

.

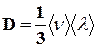Механизм возникновения внутреннего трения между параллельными слоями газа (жидкости), движущимися с различными скоростями, заключается в том, что из-за хаотического теплового движения происходит обмен молекулами между слоями, сопровождающийся переносом импульса молекул в направлении движения слоев. В результате возникает торможение слоя, движущегося быстрее, и ускорение слоя, движущегося медленнее, что и составляет суть внутреннего трения.

Экспериментально установлено, что модуль силы внутреннего трения, приложенной к слоям, подчиняется закону Ньютона:

,

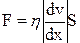где 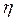- коэффициент вязкости, 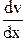- градиент скорости в направлении, перпендикулярном к слоям, 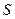- площадь слоев (рис. 7).

Коэффициент вязкости численно равен силе внутреннего трения пр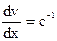и и 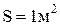. В системе СИ единицы измерения коэффициента вязкости: .

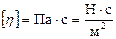Коэффициент вязкости зависит от средней скорости молекул и длины их свободного пробега:

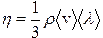. (18)

Из формулы (18) с учетом выражения (15) для средней скорости молекул получим следующее выражение для коэффициента вязкости:

.

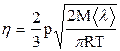ОСНОВЫ ТЕРМОДИНАМИКИ

Энтропия

Количество тепла 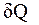, которое должно быть доставлено системе или отнято у неё при переходе от одного состояния в другое, не определяется однозначно начальным и конечным состояниями, но существенно зависит от способа осуществления этого перехода ( 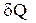не является функцией состояния системы).

Однако, приведенное количество теплоты - отношение теплоты 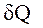к температуре 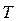системы при бесконечно малых изменениях состояния системы - есть функция состояния системы. В любом обратимом круговом процессе: 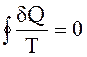. Следовательно, подинтегральное выражение есть полный дифференциал некоторой функции, которая определяется только начальным и конечным состояниями системы и не зависит от пути, каким система пришла в это состояние.

Энтропией 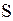называется функция состояния системы, дифференциалом которой является :

.

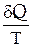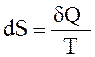Таким образом, первое начало термодинамики 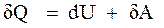можно записать в виде .

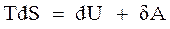В замкнутой системе для обратимых процессов 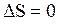; для необратимых циклов 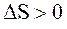. Последние два условия можно представить виде неравенства Клаузиуса: энтропия замкнутой системы может либо возрастать (в случае необратимых процессов) либо оставаться постоянной (в случае обратимых процессов):

.

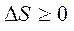Поскольку 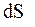и 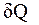имеют один и тот же знак, то по характеру изменения энтропии можно судить о направлении процесса теплообмена. При нагревании тела 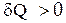и его энтропия возрастает 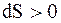, при охлаждении 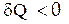и энтропия тела убывает .

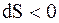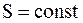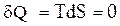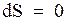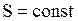Изоэнтропийным называется процесс, протекающий при постояннойэнтропии ( ). В обратимом адиабатном процессе , так что и , поэтому адиабатный процесс является изоэнтропийным.

Рассмотрим для примера идеальный газ, совершающий равновесный переход из состояния 1 в состояние 2. Изменение его энтропии

.

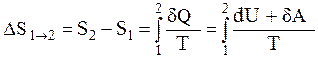Используя известные соотношения: 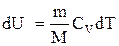; ; 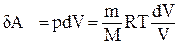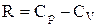и 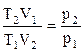, можно получить выражение 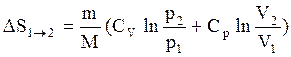, из которого видно, что изменение энтропии идеального газа при переходе его из состояния 1 в состояние 2 не зависит от вида процесса этого перехода.

Изменение энтропии в процессах идеального газа

Изохорный ( 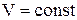)	Изобарический ( 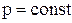)	Изотермический ( 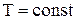)	Адиабатический ( )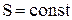

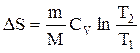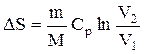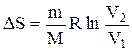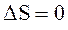Теорема Карно

Из всех периодически действующих тепловых машин, имеющих одинаковые температуры нагревателей и холодильников , наибольшим КПД обладают обратимые машины. При этом КПД обратимых машин, равны друг другу и не зависят от природы рабочего тела, а определяются только температурами нагревателя и холодильника.

Для построения рабочего цикла использует обратимые процессы. Например, цикл Карно состоит из двух изотерм (1–2, 2-4), в которых теплота полностью превращается в работу, и двух адиабат (2-3, 4–1), в которых изменение внутренней энергии полностью превращаются в работу (рис. 19).

Рассмотрим изменение энтропии рабочего тела. Общее изменение энтропии в цикле:

Так как мы рассматриваем только обратимые процессы, общее изменение энтропии .

Последовательные термодинамические процессы в цикле Карно:

Процесс	Работа	Изменение энтропии	Наблюдается
Изотермическое расширение 1—2			тело принимает теплоту
Адиабатическое расширение 2—3 ;			охлаждение до
изотермическое сжатие 3-4			тело отдает теплоту
адиабатическое сжатие ;			восстановление начального состояния

Общее изменение энтропии в равновесном цикле: , поэтому: -максимальный КПД теплового двигателя.

Следствия:

1. КПД цикла Карно не зависит от рода рабочего тела.

2. КПД определяется только разницей температур нагревателя и холодильника.

3. КПД не может быть 100% даже у идеальной тепловой машины, так как при этом температура холодильника должна быть , что запрещено законами квантовой механики и третьим законом термодинамики.

4. Невозможно создать вечный двигатель второго рода, работающий в тепловом равновесии без перепада температур, т.е. при , так как в этом случае .

Тепловые двигатели повышают энтропию замкнутой системы.

РЕАЛЬНЫЕ ГАЗЫ

Уравнение Ван-дер-Ваальса

Как показывают эксперименты, модель идеального газа позволяет описывать поведение разреженных реальных газов лишь при «нормальных» условиях, т.е. при достаточно низком давлении и высокой температуре. При высоких давлениях, или низких температурах уравнение состояния дает большие расхождения с результатами экспериментов.

При выводе уравнения состояния идеального газа не учитывались размеры молекул и потенциальная энергия их взаимодействия. Поэтому физическая природа газа не играла никакой роли и уравнение состояния универсально и применимо ко всем газам. Повышение давления приводит к уменьшению среднего расстояния между молекулами, значит, необходимо учитывать объем молекул и взаимодействие между ними.

Учитывая собственный объем молекул и силы межмолекулярного взаимодействия, Ван-дер-Ваальс вывел уравнение состояния реального газа, введя в уравнение Клапейрона-Менделеева две поправки.

1. Учет собственного объема молекул.

Для движения молекул предоставлен не весь объем , занимаемый газом, а меньший на величину объема всех молекул газа ‑ , где ‑ суммарный объем молекул газа, - молярный объем. Расчеты показывают, что константа численно равна учетверенному объему молекул, содержащихся в моле газа. Размерность поправки .

2.Учет притяжения молекул.

Действие сил притяжения молекул газа приводит к появлению дополнительного давления на газ, называемого внутренним давлением. Внутреннее давление равно

,

где – постоянная Ван-дер-Ваальса, характеризующая силы притяжения молекул. Размерность коэффициента: .

Вводя эти поправки, получим уравнение Ван-дер-Ваальса для моля газа (уравнение состояния реальных газов):

(23)

Для произвольного количества вещества газа с учетом того, что , уравнение (23) имеет вид:

где поправки и - постоянные для каждого газа величины, определяемые опытным путем.

Свойства жидкостей

Смачивание и несмачивание

На границе соприкосновения жидкостей с твердыми телами наблюдаются явления смачивания, состоящие в искривлении свободной поверхности жидкости около твердой стенки сосуда. Поверхность жидкости, искривленная на границе с твердым телом, называется мениском. Линия, по которой мениск пересекается с твердым телом, называется периметром смачивания.

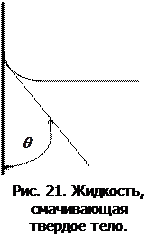Явление смачивания характеризуется краевым углом q между поверхностью твердого тела и мениском в точках их пересечения, т.е. в точках периметра смачивания. Жидкость называется смачивающей твердое тело, если краевой угол острый 0£q<p¤2 (рис. 21). Например, вода смачивает стекло, ртуть смачивает цинк. Для жидкостей, не смачивающих твердое тело, краевой угол тупой: p¤2<q<p (рис. 22). Например, вода не смачивает парафин, ртуть не смачивает стекло. Если q = 0, смачивание считается идеальным или абсолютным; q = p соответствует идеальному несмачиванию. При q = 0 и q = p наблюдается сферическая форма мениска, вогнутая или выпуклая. При q = p¤2 имеет плоскую свободную поверхность - смачивание и несмачивание отсутствует.

Различие краевых углов в явлениях смачивания и несмачивания объясняется соотношением сил притяжения между молекулами твердых тел и жидкостей и сил межмолекулярного притяжения в жидкостях. Если силы притяжения между молекулами твердого тела и жидкости больше, чем силы притяжения молекул жидкости друг к другу, то жидкость будет смачивающей. Если молекулярное притяжение в жидкости превышает силы притяжения молекул жидкости к молекулам твердого тела, то жидкость не смачивает твердое тело.

Искривление поверхности жидкости создает дополнительное (избыточное) давление на жидкость по сравнению с давлением под плоской поверхностью (Лапласово давление). Для сферической поверхности жидкости это давление выражается формулой:

,

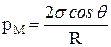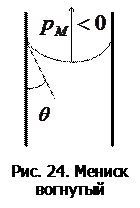
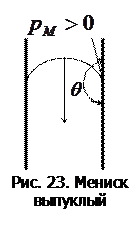где s - коэффициент поверхностного натяжения, 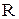– радиус сферической поверхности; 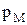> 0, если мениск выпуклый; 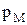< 0, если мениск вогнутый (рис. 23). При выпуклом мениске 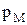увеличивает то давление, которое существует под плоской поверхностью жидкости (например, атмосферное давление на свободную поверхность жидкости). При вогнутом мениске давление под плоской поверхностью уменьшается на величину 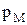(рис. 24). Дополнительное давление внутри сферического пузыря радиуса R вызывается избыточным давлением на обеих поверхностях пузыря и равно 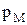= 4s ¤ R .

Капиллярные явления

Узкие цилиндрические трубки малого диаметра (< 1 мм) называются капиллярами.

Если опустить такой капилляр в несмачивающую жидкость, то под действием Лапласова давления ее уровень в капилляре понизится по сравнению с уровнем в сообщающемся с ним широком сосуде (рис. 25).

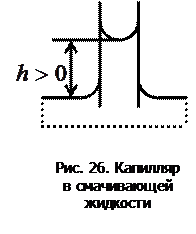
Если капилляр опустить в смачивающую жидкость, то ее уровень в капилляре по той же причине повысится (рис. 26). В случае идеального смачивания 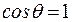, а при идеальном несмачивании 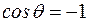. Тогда из условия равновесия жидкости 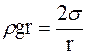можно найти высоту подъема (или опускания) жидкости в капилляре:

.

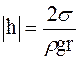Здесь 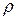- плотность жидкости, 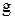– ускорение силы тяжести, 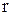– радиус капилляра. Изменения высоты уровня жидкости в капиллярах называются капиллярными явлениями. Этими явлениями объясняется гигроскопичность, т.е. способность впитывать влагу, ряда тел (вата, ткани, почвы, бетон).

Литература

1. Трофимова Т.И. Курс физики. - М.: Высш. школа, 2001.

2. Савельев И.В. Курс общей физики. Механика. Молекулярная физика.
– СПб.: Лань, 2006.

3. Сивухин Д.В. Общий курс физики. Молекулярная физика и термодинамика. - М.: Физматлит, 2005.

4. Детлаф А.А., Яворский Б.М. Курс физики. - М.: Высш. школа, 2001.

5. Федосеев В.Б. Физика: учебник. – Ростов н/Д: Феникс, 2009.

ОГЛАВЛЕНИЕ

Введение. Предмет и задачи молекулярной физики и термодинамики…………………….3

1. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ ИДЕАЛЬНЫХ ГАЗОВ……………4

1.1. Основные положения молекулярно-кинетической теории………..4

1.2. Масса и размеры молекул. Количество вещества…………………... 5

1.3. Законы идеального газа ………………………………………………..……….7

1.4. Уравнение состояния идеального газа ……………………………….…10

1.5. Основное уравнение МКТ идеальных газов …………………….…….12

1.6. Закон Максвелла о распределении молекул по скоростям.…...15

1.7. Распределение Больцмана ……………………………………………………18

1.8. Средняя длина свободного пробега молекул. Явления переноса………………………………………………………………………………20

2. ОСНОВЫ ТЕРМОДИНАМИКИ…………………………………………………………….23

2. 1. Внутренняя энергия системы Степени свободы молекул ………….23

2. 2. Первое начало термодинамики. Удельная и молярная теплоемкости .…………………………………………………………………………….26

2.3. Работа газа по перемещению поршня. Теплоемкость при постоянных объеме и давлении ……………………………………………………..27

2.4. Применение первого начала термодинамики к изопроцессам. Адиабатный процесс. Политропный процесс …………………………………..29

2.5. Круговой процесс. Обратимые и необратимые процессы………….31

2.6. Энтропия………………………………………………………………………………….33

2.7. Второе и третье начала термодинамики……………………………………..37

2.8. Тепловые двигатели и холодильные машины..………………………….38

3. РЕАЛЬНЫЕ ГАЗЫ …………………………………………………………………………….41

3.1. Уравнение Ван-дер-Ваальса …………………………………………………….41

3.2. Внутренняя энергия реального газа………………………………………….42

4. Свойства жидкостей.……………………………………………………………………...44

4.1. Особенности жидкого состояния вещества

4.2. Энергия поверхностного слоя и поверхностное натяжение жидкостей………………………………………………………………………………………45

4.3. 3 Смачивание и несмачивание………………………………………………….47

4.4. Капиллярные явления………………………………………………………………49

Литература…………………………………………………………………………………………51

молекулярная физика и термодинамика

Учебное пособие

Ростов-на-Дону 2010

УДК 530

К 91

К 91 А.Б. Гордеева, Т.П. Жданова, Н.В. Пруцакова, А.Я. Шполянский Молекулярная физика и термодинамика: Учеб. пособие. – Ростов н/Д: Издательский центр ДГТУ, 2010. – с.

Учебное пособие содержит описание основных явлений и законов молекулярной физики и термодинамики, основные положения молекулярно-кинетической теории, модели идеального и реального газов, газовые законы, первое и второе начала термодинамики, понятие энтропии, свойства жидкостей.

Цель пособия – оказать помощь студентам первого и второго курсов технических и инженерно-экономических специальностей при освоении теоретического материала, решении задач, подготовке к выполнению лабораторных работ по разделу «Молекулярная физика и термодинамика». Предназначено для студентов очной, заочной и ускоренной форм обучения.