Первое начало термодинамики. Применение I начала термодинамики к изопроцессам. Адиабатный процесс. Уравнение Пуассона. Скорость звука в газах.

Первое начало термодинамики является обобщением закона сохранения и превращения энергии для тепловых процессов. Первое начало было установлено, после того как экспериментально была доказана взаимосвязь теплоты и работы.

Первое начало термодинамики: количество теплоты, полученное системой, идет на изменение ее внутренней энергии и совершение работы над внешними телами.

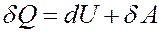(1)

где δQ – элементарное количество теплоты, δA – элементарная работа, dU – приращение внутренней энергии.

Если δQ > 0 система получает теплоту, δQ < 0 – отдает, δA > 0 – система выполняет работу над внешними телами, δA < 0 – внешние тела выполняют работу над системой.

На рис. 1 условно изображены энергетические потоки между выделенной термодинамической системой и окружающими телами. Величина Q > 0, если тепловой поток направлен в сторону термодинамической системы. Величина A > 0, если система совершает положительную работу над окружающими телами.

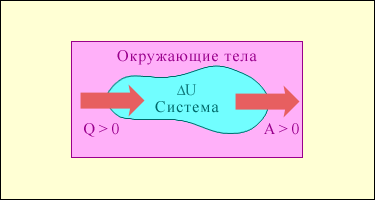Рис.1. Обмен энергией между термодинамической системой и окружающими телами в результате теплообмена и совершаемой работы.

Первый закон термодинамики является обобщением опытных фактов. Согласно этому закону, энергия не может быть создана или уничтожена; она передается от одной системы к другой и превращается из одной формы в другую.

Важным следствием первого закона термодинамики является утверждение о невозможности создания машины, способной совершать полезную работу без потребления энергии извне и без каких-либо изменений внутри самой машины. Такая гипотетическая машина получила название вечного двигателя (perpetuum mobile) первого рода. Многочисленные попытки создать такую машину неизменно заканчивались провалом. Любая машина может совершать положительную работу A над внешними телами только за счет получения некоторого количества теплоты Q от окружающих тел или уменьшения ΔU своей внутренней энергии (рис.2).

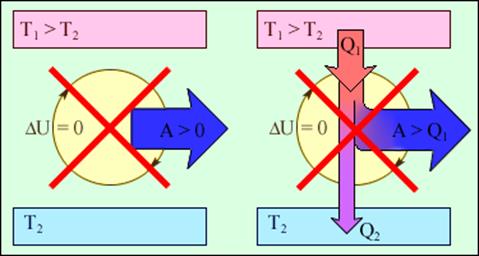
Рис.2. Циклически работающие тепловые машины, запрещаемые первым законом термодинамики: 1 – вечный двигатель 1 рода, совершающий работу без потребления энергии извне; 2 – тепловая машина с коэффициентом полезного действия η > 1.

Внутренняя энергия изолированной системы постоянная величина. Для такой системы δQ = 0, δA = 0, следовательно, dU = 0 и значит U = const.

Какие бы процессы не протекали в изолированной системе, ее внутренняя энергия остается постоянной.

Если незамкнутая система выполняет круговой процесс, т.е. в результате его система возвращается в первоначальное состояние, то dU = U₂-U₁ = 0, следовательно, из (1) δQ = δA. То есть вся теплота, полученная системой, идет на выполнение работы. Отсюда вытекает невозможность создания вечного двигателя первого рода.

Применим I начало термодинамики к изопроцессам.

1). Изотермический процесс: T = const.

Внутренняя энергия идеального газа определяется выражением:

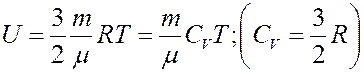(2)

где C_V – молярная теплоемкость при постоянном объеме. Определим изменение внутренней энергии.

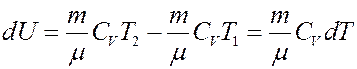(3)

Если T = const, то dU = 0 и из I начала термодинамики получим:

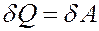
Теплота, полученная системой, идет на выполнение работы над внешними телами. Определим величину этой работы (рис.3).

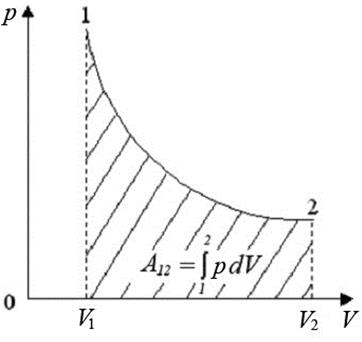
Рис.3. Изотермический процесс

Элементарная работа определяется выражением:

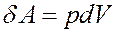
Из уравнения Клапейрона-Менделеева:

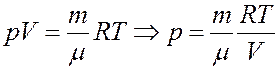
Отсюда следует:

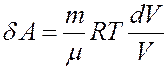(4)

Проинтегрировав (4) найдем работу:

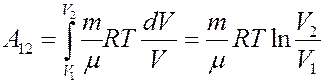(5)

Работа численно равна площади под кривой 1 → 2. При расширении V₂ > V₁, и A₁₂ > 0 система выполняет работу. При сжатии V₂ < V₁ и A₁₂ < 0 работа выполняется над системой внешними силами.

Для изотермического процесса:

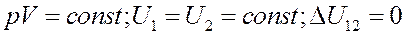
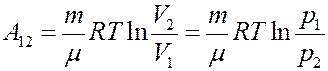
Теплоемкость при изотермическом процессе:

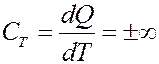
2). Изобарический процесс: p = const (рис.4)

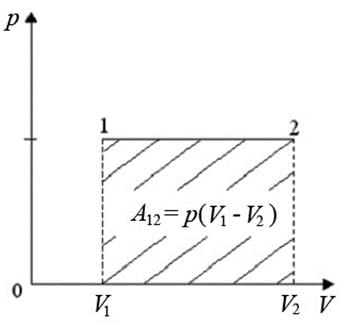
Рис.4. Изобарический процесс

Запишем I начало термодинамики:

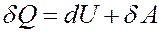
Найдем A:

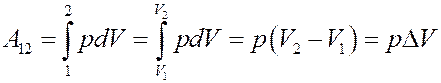(7)

Работа равна площади под кривой 1 → 2. При расширении V₂ > V₁ и A₁₂ > 0, газ выполняет работу. При сжатии V₂ < V₁ и А₁₂ < 0, работа выполняется над газом внешними силами.

Изменение внутренней энергии:

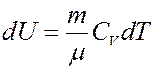
Отсюда следует:

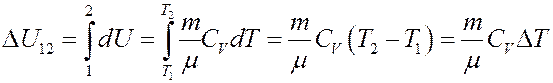(8)

С учетом этого:

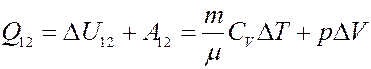(9)

Из I начала следует, что теплота, полученная системой при изобарическом процессе, частично идет на выполнение работы, и частично на изменение внутренней энергии системы. Из уравнения Клапейрона-Менделеева получим:

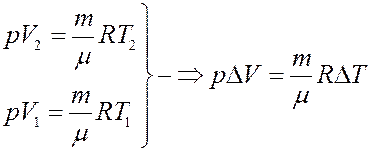
С учетом этого из (9) получим:

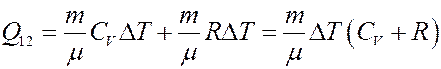(10)

Однако:

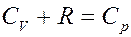(11)

(11) – уравнение Майера, где C_P – молярная теплоемкость при постоянном давлении. С учетом уравнения Майера (11) из (10) получим:

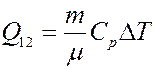(12)

Запишем I начало термодинамики:

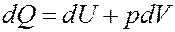
Однако:

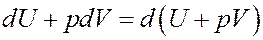
Покажем это:

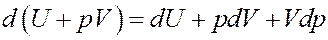
Очевидно, что Vdp = 0, т.к. p = const. Тогда I начало термодинамики можно записать следующим образом:

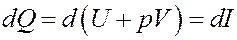(13)

где:

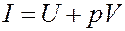(14)

Из (13) следует, что если процесс нагревания или охлаждения газа проходит при постоянном давлении, то количество теплоты, переданное газу или отданное им, будет равно изменению величины I (13, 14). Величина I называется тепловой функцией (теплосодержанием) илиэнтальпией. Для изобарического процесса:

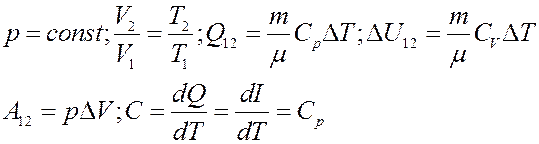
3). Изохорический процесс: V = const (рис.4):

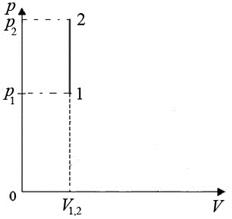
Рис.5. Изохорический процесс

Запишем I начало термодинамики:

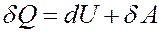
Однако:

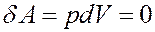
Из вышеизложенного вытекает:

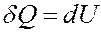
Отсюда следует, что вся теплота, подведенная к газу, идет на увеличение его внутренней энергии:

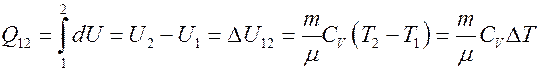(15)

Из (15) следует, что если T₂ > T₁, то Q₁₂ > 0 газ получает тепло и его внутренняя энергия увеличивается, а если T₂ < T₁ то Q₁₂ < 0, газ отдает тепло и его внутренняя энергия уменьшается.

Для изохорического процесса:

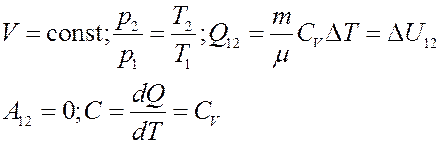
Адиабатный процесс: процесс, который происходит без теплообмена с окружающей средой, называется адиабатным (адиабатическим).

Адиабатный процесс может протекать в системе, окруженной оболочкой, теплопроводность которой равна нулю (так называемая адиабатная оболочка).

Процессы, которые протекают достаточно быстро, также будут адиабатными. Процессы теплообмена требуют некоторого времени, поэтому процессы, которые протекают достаточно быстро, можно считать процессами, проходящими без теплообмена с окружающей средой, т.е. адиабатными.

Сжатие воздуха в двигателях внутреннего сгорания, накачивание воздуха в шины автомобиля, разрежения и сжатия воздуха при распространении звуковой волны можно считать адиабатными процессами. Теплый воздух, который поднимается в верхние слои атмосферы, расширяется адиабатически, так как теплопроводность окружающего его воздуха очень мала.

Рассмотрим адиабатный процесс: δQ = 0. Запишем I начало термодинамики для адиабатного процесса:

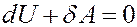
Или:

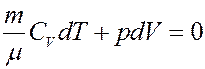(16)

Исключим из (16) температуру T, для этого запишем уравнение Клапейрона-Менделеева и продифференцируем его

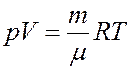
После дифференцирования получим:

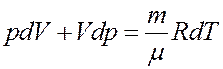
Из последнего уравнения получим:

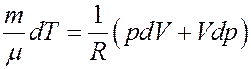(17)

Подставим (17) в(16):

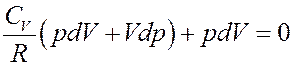
Отсюда следует, что

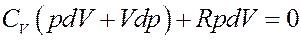
Раскроем скобки:

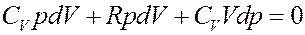(18)

Известно, что C_V + R = C_P, где C_P – молярная теплоемкость при постоянном давлении. С учетом этого перепишем (18) в виде:

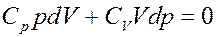(19)

Умножим (19) на величину:

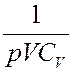
В результате получим:

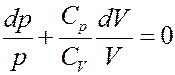(20)

Обозначим в (20)

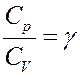
С учетом этого перепишем (20) в виде:

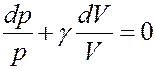(21)

Для данного газа C_p = const C_V = const, следовательно, γ = const. Учитывая это, проинтегрируем (21):

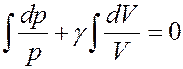
После интегрирования получим:

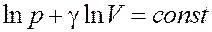
Или:

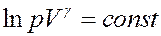
Если логарифм некоторой величины есть константа, то константой, но уже другой, является и сама эта величина:

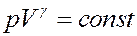(22)

Выражение (22) называется уравнением Пуассона в честь французского механика, математика и физика Симеона Дени Пуассона (1781 - 1840). Это уравнение адиабатического процесса для идеального газа, или адиабаты - кривой, описываемой этим уравнением в переменных p и V.

Величина γ называется показателем адиабаты. Строго говоря, C_p и C_V, а значит, и γ могут изменяться с изменением объема. Поэтому уравнение Пуассона справедливо для ограниченного интервала давлений и объемов. Дифференциальное уравнение (21) является точным.

С помощью уравнения Клапейрона уравнение (22) можно переписать, используя другие параметры состояния идеального газа (самостоятельно):

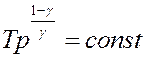(23)

Или:

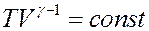(24)

Известно, что изотермический коэффициент сжимаемости идеального газа равен:

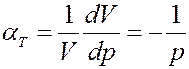(25)

Из уравнения (21) определим адиабатный коэффициент сжимаемости идеального газа:

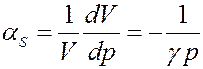(26)

Таким образом, адиабатная сжимаемость идеального газа оказывается в γ раз меньше изотермической. Это связано с тем, что при адиабатическом изменении давления изменяется, не только объем, но и температура, которая сама по себе влияет на объем.

Определим тангенсы углов наклона изотермы и адиабаты. Из (25) и (26) получим:

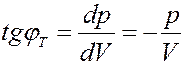(27)

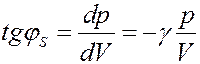(28)

Из (27) и (28) видно, что тангенс угла наклона адиабаты в γ раз больше чем изотермы (рис.6):

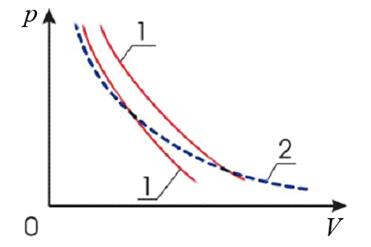
Рис.6. Графики адиабатических процессов (1) и изотермического процесса (2)

Это объясняется тем, что при адиабатическом расширении газа его давление уменьшается не только за счет увеличения объема, но и вследствие происходящего при этом уменьшения температуры газа.

При адиабатном процессе δQ = 0, значит и теплоемкость при этом процессе также равна нулю:

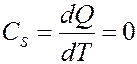
При адиабатном процессе энтропия системы не изменяется S = const, поэтому адиабатный процесс часто называют изоэнтропийным.

Определим работу, которую выполняет идеальный газ при адиабатном расширении. Из I начала термодинамики, учитывая, что δQ = 0 получим:

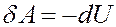
Это значит, что работа газа при адиабатном расширении, выполняется за счет уменьшения внутренней энергии газа.

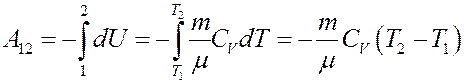
Отсюда:

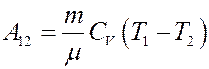(29)

Учтем, что:

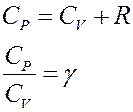
Отсюда следует:

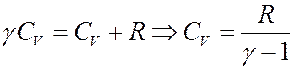
С учетом этого перепишем (29) в виде:

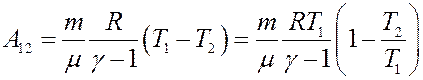
С учетом (23) и (24) из последнего уравнения получим:

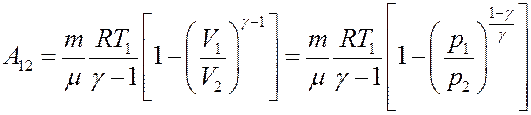(30)

Определим скорость звука в газе. Звуковые волны в газах – продольные. Из курса механики известно, что скорость распространения продольной волны в упругой среде определяется выражением:

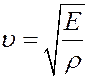(31)

где E – модуль Юнга, ρ – плотность газа. Рассмотрим столб газа высотой h вдоль вектора распространения волны. Площадь основания столба dS.

Продольная относительная деформация столба газа dh/h под действием силы dF определяется согласно закону Гука:

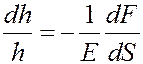
Учтем, что:

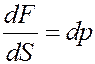
т.е. изменение давления.

Тогда:

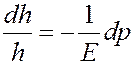
Умножим и разделим левую часть последнего уравнения на dS:

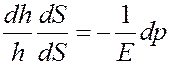
Учтем, что dhdS = dV, hdS = V, где V - объем столба газа, dV - изменение объема столба газа при изменении давления на dp. С учетом этого последнее уравнение принимает вид:

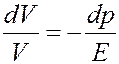(32)

Знак «-» в (32) означает, что увеличение давления (положительное dp) приводит к уменьшению объема (отрицательное dV) и наоборот. Из (32) получим:

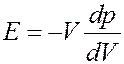(33)

Процессы разрежения и сжатия газа при распространении звуковой волны происходят быстро, поэтому их можно считать адиабатными. Тогда из уравнения (28)

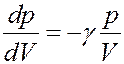
С учетом этого перепишем (33) в виде:

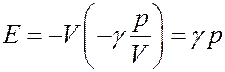(34)

С учетом (34) из (31) получим:

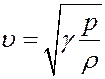(35)

Из уравнения Клапейрона-Менделеева:

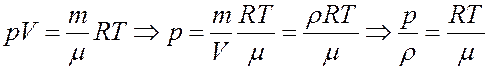
С учетом этого определим скорость звука из (35):

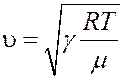(36)

Формула (36) оказывается правильной для одноатомных и двухатомных газов. В многоатомных газах наблюдается явление дисперсии – зависимость скорости звука от его частоты.

Лекция 12