Василевский С.А., Котло В.Н., Вабищевич И.А.

Василевский С.А., Котло В.Н., Вабищевич И.А.

Молекулярная физика

Курс лекций

Минск 2008

Предисловие

Настоящее учебное пособие написано в соответствии с типовой учебной программой по физике для педагогических вузов, разработанной в соответствии со стандартом высшего образования по специальности 1-02.05.04 “Физика. Дополнительная специальность”. Предлагаемый курс лекций по “Молекулярной физике и введению в термодинамику” явился результатом многолетнего опыта преподавательской деятельности авторов в БГПУ. Цель настоящего пособия изложить основные теоретические и экспериментальные вопросы молекулярной физики и термодинамики, дать в руки студентов материал, необходимый для самостоятельной работы. Особое внимание уделено объяснению физического смысла изучаемых явлений. В пособии использована полекционная нумерация формул и рисунков. Издание пособия не исключает применение других учебных пособий при изучении данного курса. Предназначено для студентов, аспирантов, преподавателей педагогических вузов.

Основы молекулярно-кинетической теории (МКТ).

Лекция 1

Предмет молекулярной физики. Основные положения молекулярно-кинетической теории (МКТ) вещества и их экспериментальное обоснование. Статистический и термодинамический подходы к изучению макроскопических систем. Флуктуации и их проявления.

В данном разделе курса общей физики, в отличие от раздела "Механика", рассматриваются закономерности, присущие большому количеству частиц. Как мы увидим в дальнейшем, количественное увеличение числа частиц в системе обуславливает качественные изменения ее свойств. Молекулярная физика и термодинамика изучают поведение макросистем.

Макросистемой называется система, состоящая из очень большого числа частиц.

Область физики, в которой изучаются физические свойства тел в различных агрегатных состояниях на основе рассмотрения их микроскопического (молекулярного) строения, называется молекулярной физикой.

В этом разделе физики рассматриваются строение и свойства газов, жидкостей и твердых тел, изменения, которые в них происходят при изменении внешних условий, фазовые превращения, явления переноса и др.

Молекулярно-кинетической теорией вещества называется учение, которое объясняет строение и свойства тел движением и взаимодействием атомов и молекул, из которых состоят тела.

Основоположником молекулярно-кинетической теории (МКТ) является М.В. Ломоносов (1711-1765 г.г.), который сформулировал ее основные положения и применил их к объяснению различных явлений.

Основные положения МКТ заключаются в следующем:

1. Все тела в природе состоят из мельчайших частиц (атомов и молекул), в состав которых входят более мелкие элементарные частицы;

2. Эти частицы находятся в непрерывном хаотическом движении, которое называется тепловым движением;

3. Между частицами вещества действуют силы притяжения и отталкивания, зависящие от расстояния между частицами.

Рассмотрим явления экспериментально подтверждающие МКТ:

1. Наличие молекул подтверждается возможностью механического дробления вещества, растворением веществ в воде и других растворителях. Очевидно, что при дроблении вещества можно получить очень маленькие частички. Наименьшая, электрически нейтральная частица вещества, сохраняющая все его химические свойства, называется молекулой. Молекулы складываются из более простых частичек – атомов. Атомом называют наименьшую частицу данного химического элемента.

Существует очень много молекул (~7000000), в то время как число атомов небольшое. В настоящее время известно 113 разных атомов. В природе существует 88 атомов, 25 получены искусственно с помощью ядерных реакций. Эти 113 атомов называются химическими элементами. Атомы химических элементов, комбинируясь друг с другом, создают миллионы существующих молекул.

2. Диффузия – самопроизвольное взаимное проникновение и перемешивание частиц двух соприкасающихся газов, жидкостей или твердых тел. Наиболее интенсивно она протекает в газах и менее интенсивно в жидкостях и твердых телах, особенно при низких температурах. Явление диффузии свидетельствует о том, что между молекулами газов, жидкостей и твердых тел есть промежутки, т.е. вещество дискретно.

Рис.1. Легкие молекулы диффундируют быстрее тяжелых

3. Смешивание разных жидкостей, растворение твердых тел в жидкостях объясняется перемешиванием молекул разного рода. При этом объем смеси может отличаться от суммарного объема компонентов смеси, что свидетельствует о разной компактности молекулярных систем:

4. Газ занимает любой предоставленный ему объем. Это значит, что молекулы газа двигаются независимо одна от другой, хаотично, беспрерывно. При этом движение молекул в любом направлении равновероятно. Это очевидно, потому что давление газа в закрытом сосуде одинаковое во всех точках объема.

5. Наиболее ярким экспериментальным подтверждением представлений МКТ о беспорядочном движении атомов и молекул является броуновское движение. Это тепловое движение мельчайших микроскопических частиц, взвешенных в жидкости или газе. Явление впервые наблюдал ботаник Броун в 1827 г., рассматривая в микроскоп взвешенные в воде споры плауна. Скорость броуновской частицы беспорядочно меняется по модулю и направлению, а ее траектория представляет собой сложную зигзагообразную кривую (рис. 2.). Теория броуновского движения была создана А. Эйнштейном (1905 г.) и М Смолуховским (1906г.). Экспериментально теория Эйнштейна была подтверждена в опытах французского физика Ж. Перрена (1908–1911 гг.). Это способствовало превращению молекулярно-кинетической гипотезы в теорию.

Рис.2. Траектория броуновской частицы

Было установлено, что скорость броуновской частички увеличивается с увеличением температуры, с уменьшением вязкости жидкости и массы частички. Броуновские частички окружены молекулами жидкости, которые движутся беспрерывно и хаотично (тепловое движение). При размерах частичек порядка 10^-4 – 10^{-5 м число ударов молекул жидкости о них не будет слишком большим. В этом случае начинают проявляться отклонения числа ударов молекул в отдельные стороны частички от средних значений.}

Отклонение тех или иных величин от их средних значений, которые происходят в малых объемах или на протяжении малых промежутков времени, называются флуктуациями.

Флуктуации скорости молекул и числа ударов приводят к тому, что импульсы, которые получает броуновская частичка с разных сторон, оказываются некомпенсированными. Частичка перемещается, изменяя величину и направление скорости.

Также как и броуновское движение, ряд физических явлений обусловлен флуктуациями соответствующих величин, которые характеризуют это явление. Так флуктуациями плотности воздуха объясняется голубой цвет неба. В атмосфере, в малых объемах беспрерывно возникают сгущения и разряжения молекул воздуха, на которых рассеивается солнечный свет. Согласно закону Релея голубые и синие лучи рассеиваются сильнее, чем желтые и красные. Поэтому цвет неба голубой, а восходящее и заходящее солнце красное. Флуктуации плотности наблюдаются вблизи критического состояния вещества. На этих флуктуациях плотности происходит интенсивное рассеяние света, получившее название критическая опалесценция.

6. В любом, даже очень маленьком объеме вещества находится огромное число молекул. Так при нормальных условиях, (p=1,01*10⁵Па, Т=273К) в 1см³ воздуха находится n_o=2.69*10¹⁹ молекул – так называемое число Лошмидта.

В молекулярно-кинетической теории количество вещества принято считать пропорциональным числу частиц. Единица количества вещества называется молем (моль).

Моль – это количество вещества, содержащее столько же частиц (молекул, атомов), сколько атомов содержится в 0,012 кг изотопа углерода ₆C¹².

Таким образом, в одном моле любого вещества содержится одно и то же число частиц (молекул). Это число называется числом Авогадро N_A:

N_A = 6,02·10²³ моль^–1.

Число Авогадро – одна из важнейших постоянных в физике.

Количество вещества ν определяется как отношение числа N частиц (молекул) вещества к постоянной Авогадро N_A:

Массу одного моля вещества принято называть молярной массой μ. Молярная масса равна произведению массы m₀ одной молекулы данного вещества на число Авогадро:

Молярная масса выражается в килограммах на моль (кг/моль). Для веществ, молекулы которых состоят из одного атома, часто используется термин атомная масса.

За единицу массы атомов и молекул принимается 1/12 массы атома изотопа углерода ₆C¹² (с массовым числом 12). Она называется атомной единицей массы (а. е. м.):

1 а. е. м. = 1,66·10^–27 кг.

Эта величина практически совпадает с массой протона или нейтрона.

Относительная атомная масса, или атомная масса химического элемента - это отношение массы атома этого элемента к 1/12 массы атома ₆C¹². Относительные атомные массы химических элементов приводятся в таблице Менделеева.

Относительная молекулярная масса вещества - это отношение массы молекулы этого вещества к 1/12 массы атома углерода ₆C¹². Зная химическую формулу вещества можно найти молекулярную массу как сумму атомных масс элементов, составляющих данное вещество. Например, у воды химическая формула H₂O, атомная масса водорода равна 1, умножаем ее на 2 и прибавляем атомную массу кислорода, 16, получаем, что молекулярная масса воды равна 18. Это безразмерное число, т. к. речь идет об относительной молекулярной массе.

Можно говорить и просто о массе атома, о массе молекулы, которые измеряют обычно в атомных единицах массы (а.е.м.). Таким образом, масса молекулы воды равна 18 а.е.м. Из определения моля следует, что молярная масса μ, выраженная в граммах, численно равна относительной молекулярной массе. Так масса одного моля воды равна 18 г.

Количество вещества (число молей) может быть рассчитано по формуле:

,

где N — число молекул в веществе массой m.

7. В конце XIX века были получены фотографии отдельных молекул и атомов Выполненные с помощью туннельного электронного микроскопа.

На рисунке слева: дефект в кристалле при разрешении в 2 ангстрема(0.2 нм). На рисунке справа - то же, но при разрешении в 1 ангстрем.

Фото атомов германия на сапфировой подложке:

Сегодня многие связывают рождение новой эпохи с 1981 годом, когда немецкие физики Герд Бинниг и Генрих Рорер создали зондовый туннельный микроскоп, позволяющий не только видеть, но и переносить с места на место отдельные атомы. Но порой нужны годы, чтобы научный прибор стал инструментом технолога. Только в 1989 году сканирующий туннельный микроскоп удалось использовать как наноманипулятор, сложив с его помощью регулярную структуру из атомов. Сотрудниики IBM Дональд Эйглер и Эрхард Швейцер выложили название своей компании 35 атомами ксенона на поверхности кристалла никеля. Эта операция заняла 22 часа и проходила при температуре вблизи абсолютного нуля (–273°С). После нагрева кристалла до –230°С буквы IBM испарились.

8. Упругость газов, очень малая сжимаемость жидкостей и твердых тел подтверждают наличие сил отталкивания между молекулами. Сохранение твердыми телами формы, необходимость приложения силы для отрыва тел от поверхности жидкости свидетельствуют о наличии сил притяжения между молекулами. На расстояниях порядка ~10^-9м между молекулами начинают действовать силы притяжения. Эти силы короткодействующие, они быстро уменьшаются с увеличением расстояния r между молекулами по закону:

,

где – a коэффициент, зависящий от строения молекул, n ≈ 7.

На расстояниях r между центрами молекул порядка ~10^-10м заметно начинают действовать силы отталкивания, которые изменяются по закону:

,

где – m ≥ 9.

Очевидно, что силы отталкивания изменяются с расстоянием быстрее, чем силы притяжения. При некотором r = r_о силы притяжения уравновешивают силы отталкивания, и их равнодействующая становится равной нулю:

.

Рис.3.Сила взаимодействия (равнодействующая) F, силы притяжения и отталкивания двух молекул. F > 0 – преобладают силы отталкивания, F < 0 – преобладают силы притяжения.

Таким образом, наиболее устойчиво молекулы размещаются на некотором минимальном расстоянии r_o. Это расстояние условно можно принять за диаметр молекулы. Потенциальная энергия взаимодействия при r = r_o минимальна. Если расстояние между молекулами достаточно велико, то преобладают силы межмолекулярного притяжения. На малых расстояниях преобладают силы отталкивания.

Число атомов и молекул в любом теле огромно. Например, в 1 м³ газа при обычных условиях содержится ~10²⁵ молекул, а в жидких и твердых телах ~10²⁸ молекул. Если считать, что движение каждого атома или молекулы подчиняется законам классической механики, то практически даже невозможно написать систему дифференциальных уравнений движения такого множества молекул (бумаги на Земле для этого не хватило бы) и решить эту систему. Поэтому поведение отдельной молекулы или атома тела не может быть изучено методами классической механики, тем более что это поведение (траектория, скорость и другие характеристики движения молекулы) изменяются со временем случайным образом.

Физические свойства макроскопических систем, состоящих из большого числа частиц, изучаются двумя взаимно дополняющими методами: статистическим и термодинамическим.

Статистический метод основан на использовании теории вероятностей и определенных моделей строения изучаемых систем. В совокупном поведении большого числа частиц, координаты и импульсы которых случайны в любой момент времени, проявляются особые статистические закономерности. Статистический метод истолковывает физические свойства макросистем, непосредственно наблюдаемые на опыте (давление, температура и т.д.) как суммарный, усредненный результат действия отдельных частиц. Например, в газах можно определить средние значения скоростей молекул и их энергий, однозначно связанных с температурой. Раздел физики, который изучает физические свойства макроскопических систем с помощью статистического метода, называется статистической физикой. Статистическая физика базируется на основных положениях молекулярно кинетической теории и изучает те параметры систем (давление, температура и т.д.), которые наблюдаются на опыте.

Термодинамика изучает свойства макроскопических систем и протекающие в них процессы, не вдаваясь в микроскопическую природу тел. Не рассматривая поведение отдельных микроскопических частиц, термодинамика позволяет сделать ряд выводов относительно протекания процессов в макросистеме, оперируя некими интегральными понятиями - параметрами (давление, температура, объем) и функциями состояния (внутренняя энергия и энтропия и др.).

Термодинамический метод основан на анализе условий и количественных соотношений, возникающих в системе при различных превращениях энергии. Соотношения между разными видами энергии позволяют изучать физические свойства исследуемых систем при самых разнообразных процессах и предсказать направления изменения состояния макросистем.

В основе термодинамики лежат несколько фундаментальных законов, называемых началами термодинамики, которые были установлены путем обобщения большого количества опытных фактов.

У статистической физики и термодинамики общий предмет изучения - свойства макросистем (веществ) и происходящие в них процессы. Подходя к изучению этих свойств и процессов с различных точек зрения, статистическая физика и термодинамика взаимно дополняют друг друга, образуя, по существу, единое целое.

Лекция 2

Лекция 3

Лекция 4

Лекция 5

Лекция 6

Явления переноса в газах

Лекция 7

Лекция 8

Внутреннее трение (вязкость газов). Теплопроводность газов.

Вязкость газов (это же касается и жидкостей) – это свойство, благодаря которому выравниваются скорости движения разных слоев газа (жидкости). Из-за вязкости сила ветра уменьшается с течением времени, успокаиваются морские волны. Выравнивание скоростей соседних слоев газа (если они разные) происходит потому, что из слоя газа с большей скоростью переносится импульс к слою газа с меньшей скоростью. Так как этот процесс связан с переносом импульса, то газ ведет себя так, как если бы на него действовала некоторая сила – сила внутреннего трения.

Ньютон установил, что при небольших скоростях (ламинарное течение) сила внутреннего трения, действующая между слоями газа (жидкости), площадью dS определяется выражением:

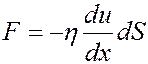(1)

где η – коэффициент динамической вязкости, du/dx – градиент скорости в направлении оси x.

Коэффициент вязкости численно равен силе внутреннего трения, действующей на единицу площади слоя (между слоями единичной площади) при единичном градиенте скорости.

Если слои газа движутся направленно с некоторой скоростью, то на хаотическое, тепловое движение молекул со скоростью 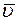накладывается направленное движение газа. Поэтому импульс каждой молекулы можно разложить на две составляющих, одна из которых обусловлена хаотическим тепловым, а вторая направленным движением молекул.

Если T = const, то составляющая импульса, обусловленная хаотическим, тепловым движением не изменяется от слоя к слою. Молекулы, которые попадают из слоя с большей скоростью направленного движения в слой с меньшей скоростью, имеют большую составляющую импульса, обусловленную направленным движением. При соударениях эти молекулы передают часть своего импульса молекулам более медленного слоя, которые увеличивают при этом скорость своего направленного движения. И наоборот молекулы более медленного слоя, попадая в более быстрый слой, при соударениях тормозят направленное движение молекул этого слоя.

Таким образом, внутреннее трение в газах обусловлено переносом импульса от слоя к слою в направлении нормали к скорости направленного движения слоев.

Пусть слои газа двигаются параллельно оси Z (рис.1.).

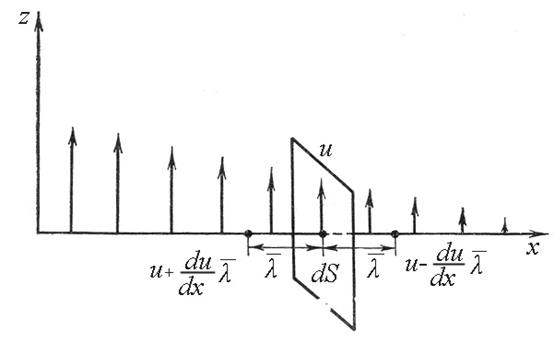
Рис.1.К определению коэффициента вязкости.

Градиент скорости вдоль оси x равен du/dx. Выберем площадку dS в слое со скоростью u. На расстояниях 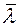от нее слева и справа скорости слоев газа будут соответственно равны:

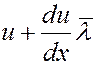
и

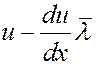
Все направления движений молекул равновероятны из-за полной их хаотичности. Поэтому в направлении оси x движется 1/3 часть всех молекул: из них 1/6 движется слева направо и 1/6 справа налево. За время dt через площадку dS слева направо пройдет

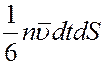
молекул, которые перенесут через эту площадку импульс:

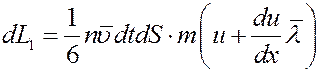(2)

Одновременно за это же время такое же количество молекул пройдет через площадку dS справа налево, при этом они перенесут импульс:

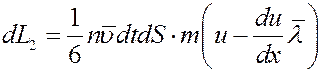(3)

За это же время из площадки dS слоя, скорость которого равна u, вылетит такое же количество молекул и вправо и влево. Но так как скорости этих молекул одинаковые, равные u и направлены в разные стороны изменение импульса слоя при этом будет равно нулю. С учетом этого импульс, который перенесется через площадку dS в положительном направлении оси x, равен:

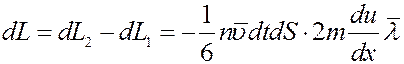(4)

Учитывая, что mn = ρ – плотность газа, из (4) получим:

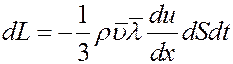(5)

Из (5) видно, что знак минус показывает, что импульс переносится в направлении уменьшения скорости слоев.

Согласно II закону Ньютона изменение импульса в единицу времени равно действующей силе:

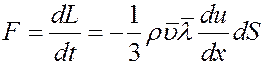(6)

Сравнивая (6) и (1) найдем коэффициент динамической вязкости:

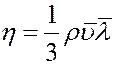(7)

В системе CI:

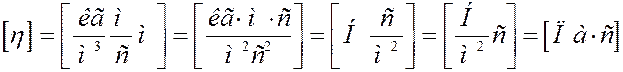
Известно, что ρ ~ p, а 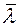~ 1/p. Следовательно, из (7) вытекает, что η не зависит от давления газа. Этот факт объясняется следующим образом. С уменьшением давления уменьшается концентрация молекул, а значит и их число, участвующее в переносе. Однако 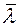при этом увеличивается. Поэтому импульс, который переносит одна молекула, так же увеличивается. В результате суммарный импульс, переносимый молекулами при данном градиенте скорости не изменяется.

Из (7) видно, что η увеличивается с ростом температуры:

.

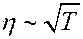На самом деле η растет несколько быстрее чем 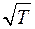, потому что с ростом температуры не только увеличивается скорость молекулы, но и уменьшается эффективный диаметр молекул (формула Сезерленда), что приводит к увеличению .

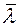Теплопроводность. Если газ неравномерно нагрет, т.е. температура одной его части больше другой, то наблюдается выравнивание температуры: более нагретая часть газа охлаждается, а более холодная нагревается. Очевидно, что выравнивание температуры связано с потоком тепла от нагретой части газа к холодной.

Явление возникновения потока тепла в газе (или в любом другом веществе) называется теплопроводностью. В любом теле, в частности в газе, предоставленном самому себе, теплопроводность приводит к выравниванию температур.

Фурье экспериментально установил, что количество теплоты, которое передается через площадку dS за время dt в направлении нормали к площадке пропорционально градиенту температуры.

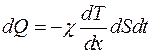(8)

где χ – коэффициент теплопроводности. Он зависит от рода газа и условий, при которых газ находится.

В системе CI:

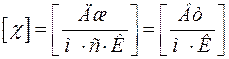
Физический смысл χ: Коэффициент теплопроводности численно равен количеству теплоты, которое переносится через единичную площадку, в единицу времени при единичном градиенте температуры.

Знак «-» в правой части (8) показывает, что направление, в котором возрастает температура и направление, в котором переносится тепло противоположные, т.е. теплота переносится в направлении уменьшения температуры.

Рассмотрим площадку dS перпендикулярную оси x, вдоль которой поддерживается постоянная разность температур. Температура слева от площадки больше чем справа T₁ > T₂ (рис.2).

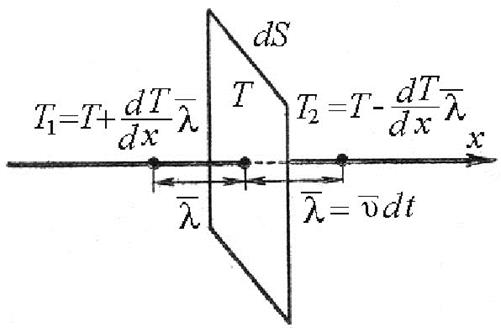
Рис.2. К определению коэффициента теплопроводности.

Через площадку dS проходят молекулы как слева направо, так и справа налево и если давление газа везде одинаково, то число молекул, которые проходят через площадку слева и справа за время dt очевидно одинаково. Однако молекулы, которые проходят слева движутся из области с более высокой температурой, чем те, которые проходят через площадку справа.

Поэтому возникает поток теплоты, равный разности энергий переносимых молекулами слева и справа. Последние столкновения перед площадкой dS слева и справа, будут происходить на расстояниях 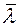, где температура слоев газа равна соответственно:

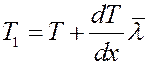
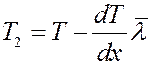
В направлении оси x двигается 1/3 всех молекул: 1/6 слева направо и 1/6 справа налево. Средняя кинетическая энергия молекул газа равна:

.

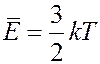За время dt через площадку dS слева направо пройдет

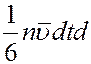
молекул, каждая из которых обладает кинетической энергией

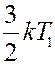
Они перенесут через площадку dS энергию:

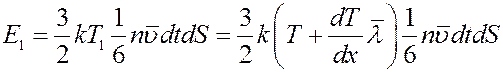(9)

Одновременно за это же время через площадку пройдет такое же количество молекул справа налево, каждая из которых обладает энергией:

.

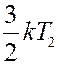Они перенесут через площадку энергию:

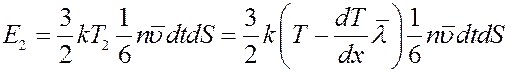(10)

С учетом этого количество теплоты (энергия), которая переносится молекулами через площадку dS, будет равна разности кинетических энергий молекул проходящих через площадку.

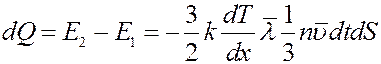(11)

Умножим и разделим правую часть (11) на массу молекулы m и число Авогадро N_A:

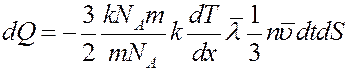(12)

Учтем, что: mn = ρ – плотность газа, а величина

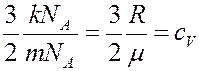
где mN_A = μ – молярная масса, c_V – удельная теплоемкость газа при постоянном объеме. С учетом этого из (12) получим:

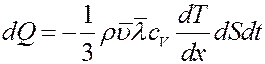(13)

Сравнивая (13) и (8) определим коэффициент теплопроводности:

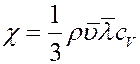(14)

Из (14) следует, что χ не зависит от давления p по той же причине, что и η (ρ ~ p, а λ ~ 1/p). Коэффициент теплопроводности зависит от T, так же как и η:

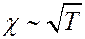
Однако для многоатомных газов необходимо учитывать некоторое возрастание теплоемкости c_V с увеличением температуры.

При определении коэффициентов переноса (D, η, χ) считалось, что молекулы двигаются через площадку в направлении нормали к ней. Однако это не так. Более строгие расчеты показывают, что через площадку двигается 1/4 часть всех молекул. С учетом этого:

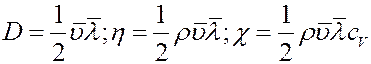
Сравнивая выражения для коэффициентов переноса, получим связь между ними:

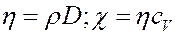
Любой из коэффициентов переноса, определенный экспериментально, позволяет найти среднюю длину свободного пробега молекул, следовательно, позволяет определить размеры (эффективный диаметр) молекул. Величины значений сечений молекул данного газа, определенные из различных коэффициентов переноса, совпадают и называются газокинетическими сечениями.

Лекция 9

Основы термодинамики

Лекция 10

Термодинамическая система (ТДС). Параметры состояния. Термодинамическое равновесие. Внутренняя энергия. Взаимодействие ТДС. Работа и теплота как форма обмена энергиями между ТДС. Равновесные и неравновесные процессы. Функции состояния и функции процесса.

Термодинамика это наука, которая изучает взаимосвязь между всеми видами энергии и влияние этой связи на свойства физических тел (систем). Особое положение термодинамики в физике связано с тем, что любая форма энергии при ее превращениях, в конце концов, переходит в энергию тепловых движений.

Термодинамика основана на двух основных законах, которые называются началами термодинамики.

Сформулируем одно из многих определений этих начал.

Первое начало термодинамики: невозможно возникновение или уничтожение энергии.

Второе начало термодинамики: невозможен процесс единственным результатом, которого было бы превращение теплоты в работу.

Американский физик Чарльз Сноу на примере 2-го начала термодинамики в книге «Две культуры» демонстрирует разрыв в культурном отношении между специалистами и неспециалистами в области естественных наук: «… и те и другие могут обсуждать произведения Шекспира, но, как только спор коснется соответствующих аспектов II-го начала термодинамики, дискуссию могут продолжать только те, кто имеет естественно-научное образование».

Чтобы было очевидно значение этих законов для науки и техники их можно сформулировать иначе. Для этого надо ввести понятие о вечном двигателе.

Двигатель, повторяющий один и тот же процесс и способный производить (выполнять) работу большую, чем полученная им энергия называется вечным двигателем первого рода.

Тепловой двигатель, повторяющий один и тот же процесс и способный целиком преобразовать в работу всю теплоту, которую он получает от других тел, называется вечным двигателем второго рода.

Было сделано множество попыток сконструировать вечный двигатель, но ни одна из них не удалась. Объяснение этому дают два начала термодинамики.

I начало: вечный двигатель первого рода не возможен.

II начало: вечный двигатель второго рода не возможен.

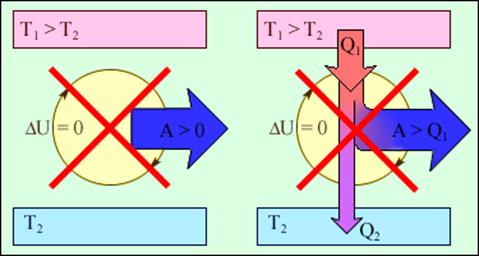
Рис.1 Циклически работающие тепловые машины, запрещаемые первым законом термодинамики: 1 – вечный двигатель 1 рода, совершающий работу без потребления энергии извне; 2 – тепловая машина с коэффициентом полезного действия η > 1.

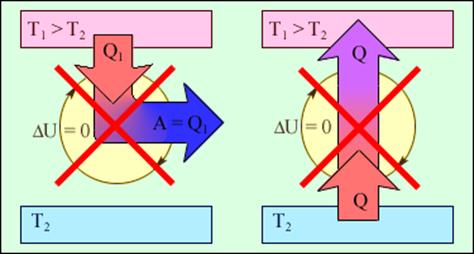
Рис.2 Процессы, не противоречащие первому закону термодинамики, но запрещаемые вторым законом: 1 – «вечный двигатель второго рода»; 2 – самопроизвольный переход тепла от холодного тела к более теплому («идеальная холодильная машина»).

Согласно вышесказанному наибольший практический интерес представляет преобразование тепловой энергии в механическую и наоборот. Однако прежде чем рассматривать эти вопросы необходимо рассмотреть термодинамическую систему, параметры ее состояния, виды процессов и т.д.

Термодинамическая система (ТДС) - это совокупность макроскопических тел, которые могут взаимодействовать между собой и с другими телами (внешней средой) - обмениваться с ними энергией и веществом. В частности, термодинамическая система может состоять из одногомакроскопического тела.

Физические величины, которые характеризуют состояние ТДС, называются термодинамическими параметрами состояния или просто параметрами состояния. Обычно в качестве параметров состояния выбирают объем V, который занимает масса вещества m, давление p и температуру T. Эти параметры не независимые. Они связаны уравнением состояния.

Самая простая ТДС – газ, который характеризуется параметрами p,V,T. Более сложная ТДС – двухфазная – жидкость, которая находится в равновесии с насыщенным паром.

ТДС могут быть частично или полностью изолированными. Если ТДС находится в теплонепроницаемой (адиабатной) оболочке она изолирована в тепловом отношении. При этом она может быть не изолирована в механическом отношении (перемещение поршня в теплоизолированном цилиндре). Если ТДС ни каким образом не взаимодействует с окружающей средой, то она полностью изолированная (замкнутая).

Система находится в термодинамическом равновесии, если макроскопические параметры, характеризующие ее состояние, остаются постоянными сколь угодно долго. Очевидно, что в состоянии равновесия не могут протекать такие процессы как диффузия, теплопередача, фазовые переходы, химические реакции и т.д.

Опыты показывают, что если параметры состояния в разных точках системы не одинаковые – нет состояния равновесия, то с течением времени система сама по себе перейдет в состояние равновесия. Процесс перехода термодинамической системы из неравновесного состояния в равновесное называется процессом релаксации, он характеризуется временем релаксации. Термодинамическое равновесие отличается от механического тем, что при неизменных макроскопических параметрах, характеризующих состояние системы, микроскопические величины – скорости, импульсы, энергия молекул беспрерывно изменяются. Тот факт, что система при этом остается в состоянии равновесия, обусловлен огромным количеством молекул.

Если процесс протекает достаточно медленно, то в любой момент система близка к своему равновесному состоянию. Такие процессы называются квазистатическими. В привычном для нас масштабе времени эти процессы могут протекать и не очень медленно. Например, разрежения и сжатия газа в звуковой волне, происходящие сотни раз в секунду, можно рассматривать как квазистатический процесс. Квазистатические процессы могут быть изображены на диаграмме состояний (например, в координатах p,V) в виде некоторой линии, каждая точка которой представляет равновесное состояние.

Любая система (тело) обладает внутренней энергией. Внутренняя энергия системы это сумма всех видов энергии, которой обладают частички системы.

Внутренняя кинетическая энергия частичек обусловлена их тепловым движением. С ростом T кинетическая энергия увеличивается. Внутренняя потенциальная энергия зависит от взаимодействия частичек. Она изменяется как при изменении T, так и при изменении агрегатного состояния системы. Для тела (системы) внутренняя энергия тем больше, чем больше в нем находится частичек, т.е. чем больше масса тела. Следовательно, внутренняя энергия величина аддитивная.

Определим внутреннюю энергию идеального газа массой m. Энергия одной молекулы:

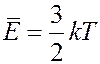(1)

Для газа массой m:

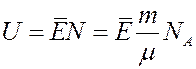(2)

где N – число молекул в массе газа m.

С учетом (1) из (2) получим:

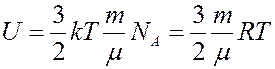(3).

К внутренней энергии также относится внутриядерная энергия, эйнштейновская энергия покоя E_o= mc². Однако в большинстве задач термодинамики эти виды энергии остаются постоянными. На них можно не обращать внимания, так как в термодинамике важно не абсолютное значение внутренней энергии, а ее изменение, которое происходит в разных процессах.

Очевидно, что внутренняя энергия однозначно является функцией параметров состояния. Если система в результате каких-либо процессов, в которых изменяются ее параметры состояния, возвратилась в первоначальное состояние, то при этом изменение внутренней энергии равно нулю ΔU = 0. С математической точки зрения это означает, что внутренняя энергия является полным дифференциалом функции параметров состояния. Следовательно, изменение внутренней энергии при переходе системы из одного состояния в другое всегда будет равно разности внутренних энергий в этих состояниях, и не будет зависеть от вида процесса перехода системы из одного состояния в другое.

В природе, на практике ТДС взаимодействуют между собой, при этом изменяются их параметры состояния, их внутренние энергии. В завис