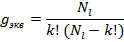Особенности спектральных термов в приближении “L-S” связи.

В приближении центрального поля энергия атома полностью определяется заданием электронной конфигурации, т.е. заданием n l для каждого электрона.

Каждой электронной конфигурации ( 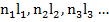) соответствует 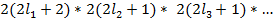состояний. Все эти состояния различаются значениями 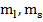. Отнесение этих состояний к одному и тому же энергетическому уровню возможно до тех пор, пока мы не учитываем спин-орбитальное или электростатическое взаимодействие. Учет этих взаимодействий приводит к расщеплению уровней на ряд подуровней. Электростатическое взаимодействие приводит к расщеплению уровня, соответствующего данной электронной конфигурации на ряд подуровней, характеризуемых различными значениями полного орбитального момента электронов и спина.

Физический смысл зависимости энергии расщепления от L

Различным значениям L соответствует различная ориентация орбитальных моментов отдельных электронов.

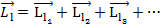
В состояниях с различными значениями L электроны находятся на разных расстояниях друг от друга, поэтому различной будет энергия электростатического отталкивания. Энергия взаимодействия электронов с ядром и энергия взаимодействия электронов друг с другом имеют разные знаки, поэтому электростатическое взаимодействие приводит к сдвигу энергетических уровней вверх ( Значение энергии по абсолютной величине уменьшается).

Эмпирически было установлено, что для основных конфигураций и для конфигураций, содержащих эквивалентные электроны, расщепление уровней при электростатическом взаимодействии подчиняется правилу Хунда, которое гласит, что:

наименьшей энергией обладает уровень с наибольшим возможным для данной электронной конфигурации значением квантового числа полного спинового момента S и наибольшим возможным для данного S значением орбитального квантового числа L.

Состояние с наименьшей энергией в атоме называется основным.

Уровни энергии, соответствующие определенным значениям L и S, называются спектральными термами.

Для обозначения термов используют заглавные буквы латинского алфавита.

Если 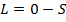, , 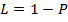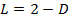. И.т.д.

Релятивистские эффекты, в частности спин-орбитальное взаимодействие, приводят к расщеплению каждого терма на ряд компонент, соответствующих значениям полного механического момента атома.

Полный механический момент - 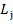, где j – квантовое число полного механического момента.

Расщепление терма в результате спин-орбитального взаимодействия называется тонким или мультиплетным.

Квантовое число полного момента может принимать значения: ;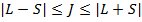

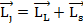
Если L>S => всего (2S+1) значение J => каждый терм расщепляется на (2S+1) компоненту.

Если L<S=> всего (2L+1) значение J => каждый терм расщепляется на (2L+1) компоненту.

Мультиплетность: .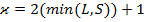

Полное обозначение терма: .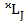

В зависимости от того, на сколько компонент расщепляется терм при спин-орбитальном взаимодействии, термы подразделяют на синглетные, дуплетные и триплетные.

Каждому терму с L и S относится (2L+1)(2S+1) состояний, отличающихся значением квантовых чисел проекций орбитального и спинового моментов, поэтому состояние многоэлектронного атома будет вырождено.

Энергия изолированного атома не может зависеть от того, как полный механический момент атома ориентирован в пространстве, следовательно, каждая j-тая компонента терма вырождена с кратностью вырождения 2J+1 и статистический вес состояния равен:

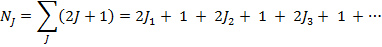
C другой стороны:

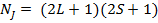, т.е. учёт спин-орбитального взаимодействия не меняет числа состояний, относящихся к терму LS

Мультиплетное расщепление подчиняется правилу интервалов Ланде, которое гласит:

1) расщепление уровней с квантовыми числами J, J-1 пропорционально J

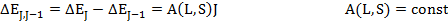
2) A(L,S) – постоянная мультиплетного расщепления. Зависит от квантовых чисел L и S и может быть как положительной, так и отрицательной.

· Если при A>0, наименьшим значением энергии обладает с наименьшим большим возможным значением J=L-S , то такие мультиплеты называются нормальными.

· Если при A<0 наименьшим значением энергии обладает компонента мультиплета с наибольшим возможным значением J=L+S, то такие мультиплеты называются обращенными.

Эмпирически было установлено, что для конфигурации атомов, содержащих n эквивалентных электронов, справедлива закономерность:

· если n<(2l+1), т.е. оболочка заполнена менее чем на половину, то для такого атома будет наблюдаться нормальный мультиплет

· если n>(2l+1), т.е. оболочка заполнена более чем на половину, то для такого атома будет наблюдаться обращенный мультиплет

· если n=(2l+1), мультиплетное расщепление отсутствует

Группировка уровней, типичная для L-S связи:

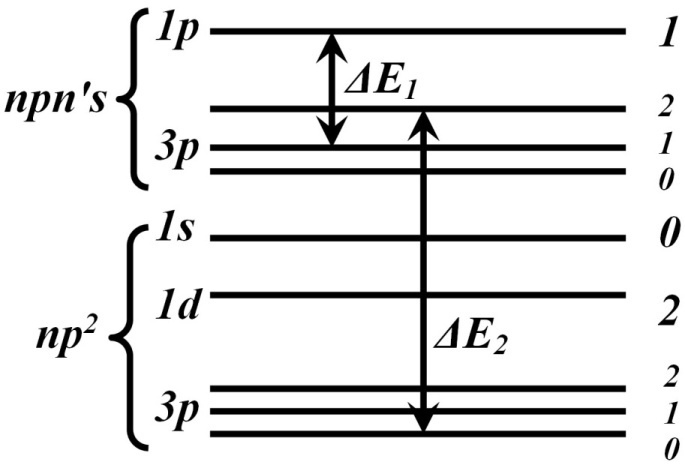
Расстояние между термами одной электронной конфигурации значительно меньше, чем расстояние между одинаковыми термами различных конфигураций: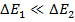

Каждый терм, за исключением синглетных и S-термов, имеет тонкую структуру, причем расстояние между компонентами этой структуры значительно меньше, чем расстояние между различными термами.

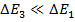
L-S связь называется связью Рассела-Саундерса, или нормальной связью.

Нахождение термов многоэлектронной конфигурации, состоящей из неэквивалентных электронов:

Все возможные термы легко получить на основании общего квантовомеханического правила сложения моментов.

1) Находим орбитальный механический момент системы: ,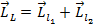

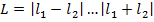
2) Находим спиновой механический момент системы: ,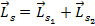

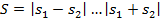
3) ,

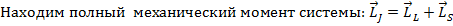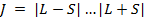
Состояние записываем в виде:

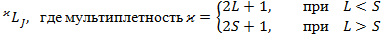
Сложение производится сначала для двух электронов, а затем к получившимся термам последовательно присоединяются по одному электрону.

Пример Найти всевозможные термы для конфигурации npn’p’, а затемдля конфигурацииnpn’p’n’’p’’

Добавление 1 электрона к синглетным термам даёт дублетные термы, к дублетным – синглетные и триплетные, к триплетным – дублетные и квартетные.

Существует простой приём определить мультиплетность термов, состоящих из неэквивалентных электронов: добавляя к терму данной конфигурации электрон, мы получим термы с мультиплетностью на единицу больше и единицу меньше исходной.

Часто указывается статистический вес конфигурации. Статистическим весом конфигурации называется полное число состояний, относящихся к данной электронной конфигурации. Для конфигурации, содержащей неэквивалентные электроны:

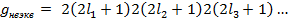
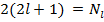Для конфигураций из k эквивалентных электронов статистический вес определяется числом возможных комбинаций, которые можно составить из квантовых чисел с учетом принципа Паули. Число таких комбинаций равно числу сочетаний из по k: