Сериальные закономерности атомных спектров.

Сериальные закономерности атомных спектров.

Атомам каждого вещества присущ определенный вид спектра. Все атомные спектры линейчаты и не зависят от способа их возбуждения. Обычно отдельные линии в спектре могут быть объединены в серии.

Спектральной серией называется совокупность спектральных линий, соответствующих переходам с одного и того же энергетического уровня спектра поглощения или на один и тот же уровень спектра испускания.

Каждое состояние электрона в атоме водорода можно охарактеризовать тремя квантовыми числами: n – главное квантовое число, определяющее энергию состояния, может принимать любые значения, начиная с единицы; l – орбитальное квантовое число, определяющее значение орбитального момента количества движения ( 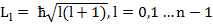); m – магнитное квантовое число, определяющее проекцию орбитального момента импульса на выбранное направление (m = -l,…0,…l, всего 2l+1 значение).

Энергия атома в состоянии (n,l,m) однозначно определяется значением n в кулоновском поле и не зависит от квантовых чисел l и m до тех пор, пока не учитываем спин-орбитальное взаимодействие, следовательно, для частицы в кулоновском поле характерно 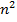- кратное вырождение уровней.

В спектроскопии принято обозначение состояния электрона по значению орбитального квантового числа малыми латинскими буквами: l = 0 – s-состояние, l = 1 – p-состояние, l = 2 – d, l=3 – f, l = 4 – g, l = 5 – h.

Между состояниями с квантовыми числами (n,l,m) и (n’,l’,m’) возможны переходы. Если переход сопровождается излучением фотона, то такой переход называется радиационным или излучательным. Для радиационных переходов выполняется правило отбора: ∆l = l’ – l = ±1, ∆m = m’ – m = 0, ±1.

Переходы, для которых выполняется правило отбора, называются разрешенными.

В спектре излучения атома водорода отчетливо наблюдаются спектральные серии.

[1/λ] = [ 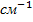], 1/λ = R(1/ - 1/ ), n = 2,3,4… - серия Лаймана. R = 109677,581 .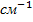

В серии Лаймана отчетливо наблюдаются линии .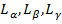

1/λ = R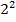(1/ - 1/ ), n = 3,4,5… - серия Бальмера. Линии .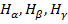

1/λ = R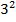(1/ - 1/ ), n = 4,5,6… - серия Пашена

1/λ = R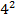(1/ - 1/ ), n = 5,6,7… - серия Брэккета

1/λ = R(1/ 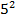- 1/ ), n = 6,7,8… - серия Пфунда

Для любых двух уровней с квантовыми числами n и n' существуют состояния, между которыми возможны радиационные переходы.

В спектре излучения любого атома выделяют и часто используют резонансную линию – линию, соответствующую переходу из основного состояния в первое возбужденное в спектре поглощения и наоборот в спектре испускания.

Резонансной линией водорода является главная линия серии Лаймана 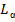, соответствующая переходу из n = 1 в n = 2 ( 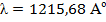). Основными линиями ближнего УФ – спектра являются линии серии Бальмера:

,

,

.

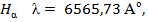
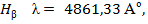
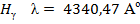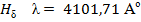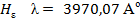Сериальные закономерности атомных спектров.

Атомам каждого вещества присущ определенный вид спектра. Все атомные спектры линейчаты и не зависят от способа их возбуждения. Обычно отдельные линии в спектре могут быть объединены в серии.

Спектральной серией называется совокупность спектральных линий, соответствующих переходам с одного и того же энергетического уровня спектра поглощения или на один и тот же уровень спектра испускания.

Каждое состояние электрона в атоме водорода можно охарактеризовать тремя квантовыми числами: n – главное квантовое число, определяющее энергию состояния, может принимать любые значения, начиная с единицы; l – орбитальное квантовое число, определяющее значение орбитального момента количества движения ( 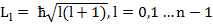); m – магнитное квантовое число, определяющее проекцию орбитального момента импульса на выбранное направление (m = -l,…0,…l, всего 2l+1 значение).

Энергия атома в состоянии (n,l,m) однозначно определяется значением n в кулоновском поле и не зависит от квантовых чисел l и m до тех пор, пока не учитываем спин-орбитальное взаимодействие, следовательно, для частицы в кулоновском поле характерно 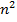- кратное вырождение уровней.

В спектроскопии принято обозначение состояния электрона по значению орбитального квантового числа малыми латинскими буквами: l = 0 – s-состояние, l = 1 – p-состояние, l = 2 – d, l=3 – f, l = 4 – g, l = 5 – h.

Между состояниями с квантовыми числами (n,l,m) и (n’,l’,m’) возможны переходы. Если переход сопровождается излучением фотона, то такой переход называется радиационным или излучательным. Для радиационных переходов выполняется правило отбора: ∆l = l’ – l = ±1, ∆m = m’ – m = 0, ±1.

Переходы, для которых выполняется правило отбора, называются разрешенными.

В спектре излучения атома водорода отчетливо наблюдаются спектральные серии.

[1/λ] = [ 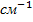], 1/λ = R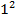(1/ - 1/ ), n = 2,3,4… - серия Лаймана. R = 109677,581 .

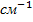В серии Лаймана отчетливо наблюдаются линии .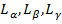

1/λ = R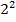(1/ - 1/ ), n = 3,4,5… - серия Бальмера. Линии .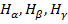

1/λ = R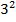(1/ - 1/ ), n = 4,5,6… - серия Пашена

1/λ = R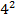(1/ - 1/ ), n = 5,6,7… - серия Брэккета

1/λ = R(1/ 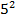- 1/ ), n = 6,7,8… - серия Пфунда

Для любых двух уровней с квантовыми числами n и n' существуют состояния, между которыми возможны радиационные переходы.

В спектре излучения любого атома выделяют и часто используют резонансную линию – линию, соответствующую переходу из основного состояния в первое возбужденное в спектре поглощения и наоборот в спектре испускания.

Резонансной линией водорода является главная линия серии Лаймана 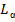, соответствующая переходу из n = 1 в n = 2 ( 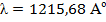). Основными линиями ближнего УФ – спектра являются линии серии Бальмера:

,

,

.
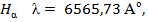
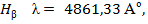
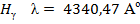
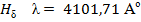
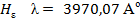