Молярная электрическая проводимость
Молярная электрическая проводимость раствора электролита - это электрическая проводимость такого объема раствора, который содержит 1моль растворенного вещества и заключен между двумя параллельными электродами, расположенными на расстоянии  друг от друга, причем каждый электрод имеет такую площадь, чтобы в этом объеме содержался 1моль растворенного вещества (т. е площадь должна быть тем больше, чем меньше концентрация раствора).
друг от друга, причем каждый электрод имеет такую площадь, чтобы в этом объеме содержался 1моль растворенного вещества (т. е площадь должна быть тем больше, чем меньше концентрация раствора).
Молярная электрическая проводимость 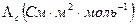 связана с удельной соотношением
связана с удельной соотношением
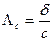 , (33.4)
, (33.4)
где  удельная электрическая проводимость, См/м; c - концентрация,
удельная электрическая проводимость, См/м; c - концентрация, 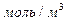 .
.
При выражении концентрации раствора в моль/л уравнение (8.4) записывается в виде
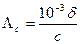 . (33.5)
. (33.5)
Исходя из уравнений (8.3) и (8.5) с учетом, для бинарного электролита, следует
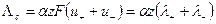 . (33.6)
. (33.6)
Ход кривых концентрационной зависимости, молярной электрической проводимости растворов электролитов, показан на рис. 3.
При c = 0 молярная проводимость раствора не равна молярной проводимости чистого растворителя 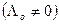 . Величина
. Величина 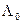 называемая предельной электрической проводимостью [1]проводимостью6и отвечает электрической проводимости гипотетического бесконечно разбавленного раствора, характеризующегося полной диссоциацией электролита и отсутствием сил электростатического взаимодействия между ионами.
называемая предельной электрической проводимостью [1]проводимостью6и отвечает электрической проводимости гипотетического бесконечно разбавленного раствора, характеризующегося полной диссоциацией электролита и отсутствием сил электростатического взаимодействия между ионами.
При росте концентрации молярная проводимость растворов и сильных и слабых электролитов уменьшается 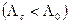 .
.
У сильных электролитов 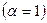 количество заряженных частиц, способных
количество заряженных частиц, способных
участвовать в переносе тока, при любой концентрации остается постоянной. Некоторое уменьшение молярной проводимости с ростом концентрации происходит только под влиянием тормозящих эффектов и вследствие увеличения вязкости растворов.
Молярная проводимость растворов сильных электролитов в области малых концентраций линейно зависит от корня квадратного из концентрации (рис. 3) и может быть описана эмпирическим уравнением
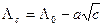 , (33.7)
, (33.7)
где a - эмпирическая константа. Уравнение (33.7) называют уравнением Колрауша или законом квадратного корня. С достаточной степенью точности 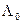 может быть определена экспериментально экстраполяцией линейной зависимости
может быть определена экспериментально экстраполяцией линейной зависимости 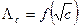 на бесконечное разведение (рис. 3). При несколько более высоких концентрациях сильных электролитов лучшее согласие с опытом дает уравнение
на бесконечное разведение (рис. 3). При несколько более высоких концентрациях сильных электролитов лучшее согласие с опытом дает уравнение
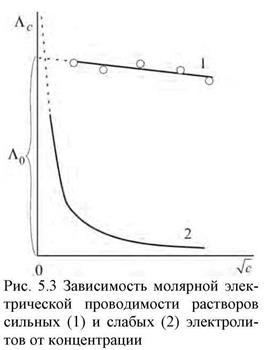 | 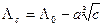 (33.8) известное под названием закона кубического корня. Для выражения зависимости молярной электрической проводимости растворов электролитов от концентрации предложен ряд уравнений, в которые входят константы, полученные с учетом сил релаксационного и электрофоретического торможения и зависящие от диэлектрической проницаемости, вязкости растворителя и температуры. Таковы, например, константы А и B в формуле Шидловского (33.8) известное под названием закона кубического корня. Для выражения зависимости молярной электрической проводимости растворов электролитов от концентрации предложен ряд уравнений, в которые входят константы, полученные с учетом сил релаксационного и электрофоретического торможения и зависящие от диэлектрической проницаемости, вязкости растворителя и температуры. Таковы, например, константы А и B в формуле Шидловского 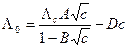 , (33.9) , (33.9) |
которая является наиболее удачной среди эмпирических формулам, является для концентрированных растворов пользуются (в ней D - эмпирический коэффициент).
У слабых электролитов, в соответствии с законом разведения Оствальда, количество заряженных частиц в растворе резко уменьшается вследствие ассоциации 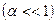 и соответственно наблюдается резкое понижение молярной проводимости.
и соответственно наблюдается резкое понижение молярной проводимости.
Зависимость 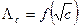 для растворов слабых электролитов нелинейна (рис. 3). Для разбавленных растворов слабых электролитов справедливо уравнение
для растворов слабых электролитов нелинейна (рис. 3). Для разбавленных растворов слабых электролитов справедливо уравнение
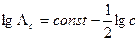 (33.10)
(33.10)
При уменьшении концентрации 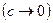 кривая, выражающая эту зависимость, асимптотически приближается к ординате, и
кривая, выражающая эту зависимость, асимптотически приближается к ординате, и  слабого электролита может быть больше
слабого электролита может быть больше 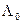 сильного электролита.
сильного электролита.
В случае слабых электролитов 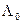 нельзя определить экспериментально. Ее находят по закону независимости движения ионов при бесконечном разбавлении (закону Кольрауша). Согласно этому закону, справедливому как для сильных, так и для слабых электролитов, при бесконечном разбавлении, когда
нельзя определить экспериментально. Ее находят по закону независимости движения ионов при бесконечном разбавлении (закону Кольрауша). Согласно этому закону, справедливому как для сильных, так и для слабых электролитов, при бесконечном разбавлении, когда  молярная электрическая проводимость равна сумме молярной электрических проводимостей ионов (подвижностей).
молярная электрическая проводимость равна сумме молярной электрических проводимостей ионов (подвижностей).
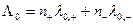 , (33.11)
, (33.11)
Где 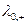 и
и 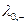 - предельная молярная электрической проводимость катиона и аниона;
- предельная молярная электрической проводимость катиона и аниона; 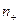 и
и 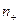 - количества катионов и анионов в растворе, соответственно.
- количества катионов и анионов в растворе, соответственно.
Применительно к 1,1-электролиту
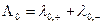 . (33.12)
. (33.12)
Все сказанное выше позволяет сделать два практически важных заключения. Во-первых, выражения для чисел переноса справедливы также и для предельно разбавленных растворов. Исходя из этого с учетом закона независимости движения ионов Кольрауша можно записать
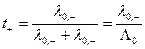 и
и 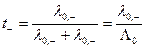 . (33.13)
. (33.13)
Во-вторых, закон Кольрауша дает возможность по известным значениям 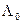 для некоторых электролитов расчетным путем найти значение
для некоторых электролитов расчетным путем найти значение 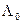 для данного электролита, если он состоит из тех же ионов. Таким образом, определяя значения
для данного электролита, если он состоит из тех же ионов. Таким образом, определяя значения 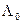 для ряда сильных электролитов графическим методом из экспериментальных данных (рис. 3), можно рассчитать значение
для ряда сильных электролитов графическим методом из экспериментальных данных (рис. 3), можно рассчитать значение 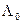 для слабого электролита. Например,
для слабого электролита. Например,
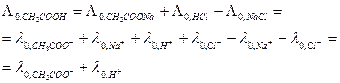
(33.14)
где 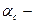 степень диссоциации при данной концентрации c;
степень диссоциации при данной концентрации c;
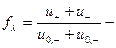 коэффициент электрической проводимости, введенный Бьеррумом и вносящий поправку на силы взаимодействия при прохождении тока через растворы электролитов. Межионное взаимодействие при неравновесных процессах, в частности при прохождении электрического тока через растворы электролитов (явление электрической проводимости), должно иметь иной характер, чем в условиях равновесия. Поэтому коэффициент электрической проводимости отличается от коэффициента активности, относящегося только к равновесным растворам.
коэффициент электрической проводимости, введенный Бьеррумом и вносящий поправку на силы взаимодействия при прохождении тока через растворы электролитов. Межионное взаимодействие при неравновесных процессах, в частности при прохождении электрического тока через растворы электролитов (явление электрической проводимости), должно иметь иной характер, чем в условиях равновесия. Поэтому коэффициент электрической проводимости отличается от коэффициента активности, относящегося только к равновесным растворам.
Для слабых электролитов подвижности ионов в разбавленных и в бесконечно разбавленных растворах близки между собой  , поэтому для них
, поэтому для них
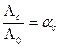 (33.15)
(33.15)
Для сильных электролитов, диссоциирующих полностью 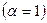
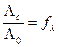 . (33.16)
. (33.16)
Предмет электрохимии
Предметом электрохимии, по определению А. Н. Фрумкина, является изучение превращения веществ на границе раздела проводников электричества первого рода и второго рода, происходящие с участием свободных электронов. Эти превращения и называют электрохимическими реакциями. Особенность их состоит в том, что это реакции эти реакции протекают не на такой гетерогенной границе, на которой электронная проводимость электрического тока заменяется ионной.
Если опустить кусок металлического цинка в раствор водный раствор соляной кислоты, то произойдет окисление атомов цинка и восстановление ионов водорода:
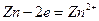

Гетерогенную химическую реакцию  можно провести и не приводя в соприкосновение цинк и соляную кислоту - если в одну часть сосуда, разделенного диафрагмой[2] налить раствор хлорида цинка и погрузить в него пластину металлического цинка, а в другую часть - соляную кислоту и погрузить в нее платиновую пластину, замкнув пластины проводником первого рода.
можно провести и не приводя в соприкосновение цинк и соляную кислоту - если в одну часть сосуда, разделенного диафрагмой[2] налить раствор хлорида цинка и погрузить в него пластину металлического цинка, а в другую часть - соляную кислоту и погрузить в нее платиновую пластину, замкнув пластины проводником первого рода.
После замыкания пластин на границе цинк-раствор начнется самопроизвольные реакции окисление цинка (анодный процесс), а на границе платина-соляная кислота- восстановления ионов водорода (катодный процесс). Ионы же хлора не участвуют в электрохимических реакциях. При протекании химической реакции электроны не образуются и не исчезают, а только переходят от одной частицы к другой, поэтому окислительное и восстановительное превращения должны всегда протекать одновременной и в эквивалентных количествах.
Ионы, непосредственно участвующие в электрохимических реакциях (в данном случае 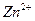 и
и  ), называют потенциал-определяющими ионами. Ионы же хлора в этих реакциях не участвуют.
), называют потенциал-определяющими ионами. Ионы же хлора в этих реакциях не участвуют.
Проводник первого рода, находящийся в контакте с проводником второго рода, называется электродом, а ионопроводящая среда в электрохимической системе называется электролитом. Этим же термином обозначают обычно и вещество, ионы которого переносят ток.
Такая система, которая состоит из проводников первого рода и находящихся в соприкосновении с ними проводников второго рода называется электрохимической системой[3].
