Методы проведения эксперимента и обработки результатов наблюдений

10.1 Основные понятия и определения

Результаты эксперимента химии и химической технологии были и остаются данным критерием при решении практических задач и проверке теоретических гипотез.

Для решения различного рода задач применяют экспериментально-статистические методы. Эффективность и информативность экспериментов зависит от природы их проведения. Различают пассивный и активный эксперименты. Пассивный эксперимент является методом, когда влияние одного фактора определяется в результате его варьирования при постоянстве других факторов. Активный эксперимент применяется, когда условия его проведения меняются по определенному плану.

Планирование эксперимента - это процедура выбора числа и условий проведения опытов, необходимых и достаточных для решения поставленной задачи с требуемой точностью.

Основу пассивного и активного экспериментов составляет статистическая обработка результатов, применяемая в статистическом анализе. Статистические методы анализа основаны на вероятном подходе при определении числовых характеристик совокупности случайных величин. Принято считать, что результаты экспериментов являются случайными величинами, так как зависят от большого числа неучтенных факторов. В результате этого невозможно получить истинное значение при измерении какой-либо величины. Разность между истиной величиной и приближенной, полученной по результатам наблюдений, называется ошибкой измерения. Обычно ошибка измерения и истинная величина неизвестны. Их значения оцениваются статистической обработкой результатов эксперимента. Существуют различного рода ошибки.

Абсолютная ошибка - разница между истинным значением измеряемой величины и полученным результатом.

Относительная ошибка - отношение абсолютной ошибки к среднему значению измеряемой величины.

Случайная ошибка - неизбежная ошибка при повторных измерениях, которая принимает различные значения.

Систематическая ошибка - это ошибка, которая может быть связана с неточностями приборов, особенностями экспериментатора, методикой проведении опытов.

Грубые ошибки возникают вследствие нарушений основных условий измерений. При обработке измерений выявленные промахи или грубые результаты в расчет не включают.

Оценка случайной величины, как правило, производится но ограниченному числу наблюдений. Существуют понятия генеральной и выборочной совокупности, генеральная состоит из всех мыслимых в данных условиях измерений, выборочная - из ограниченного числа измерений.

Под измерением понимается сравнение измеряемой величины с другой величиной, принятой за единицу измерения. Измерения разделяют на прямые и косвенные. При прямых определяемая величина сравнивается с единицей измерения непосредственно или при помощи измерительного прибора, проградуированного в соответствующих единицах. При косвенных измеряемая величина определяется из результатов прямых измерений других величин, которые связаны с измеряемой величиной функциональной зависимостью. Например, измерения плотности материала по измерениям массы и объема материала.

Важнейшими характеристиками случайных величин являются среднее значение, дисперсия, среднее квадратичное отклонение. Дисперсия ( 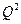- для генеральной совокупности и - для выборки) характеризует степень разброса полученных результатов относительно среднего значения измерений

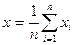
Для генеральной совокупности дисперсию 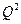вычисляют по формуле

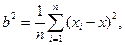
а для выборки -

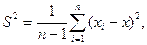
где x_i - измеряемое значение случайной величины; х - среднее значение из всех чисел х_i, п - число всех измерений.

Упрощенная формула для вычисления имеет вид

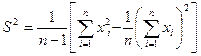
Среднее квадратичное отклонение отдельного измеренного значения определяют пo формуле:

,

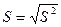а среднее квадратичное отклонение среднего результата –

.

Для оценки истинного значения измеряемой величины необходимо знать ее среднее значение х и границы интервала которые с заданной вероятностью 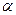покрывает истинное значение. Границы доверительною интервала при выбранной вероятности 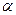определяют по формуле:

или ,

где - критерий (коэффициент Стьюдента) (таблица 10.1); - число степеней свободы.

Таблица 10.1 – Коэффициенты Стьюдента

	6,31 2,92 2,35 2,13 2,02 1,95 1,89 1,86 1,83	12,7 4,30 3,18 2,78 2,57 2,45 2,36 2,31 2,26

Зная доверительный интервал, можно определить относительную ошибку измерений:

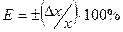
Если серия измерений содержит значение, оцениваемое как грубое, то необходимо проверить, не является ли это следствием статистического разброса измерений. Исключение грубого значения проводят по 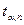- критерию (таблица 10.2):

или

Если расчетное значение не больше, найденного по таблице 10.2, то значение измерения, оцениваемое как «грубое», считают следствием статистического разброса и из расчета не исключают.

Таблица 10.2 – Значение 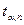- критерия для выявления «грубых» результатов

n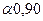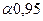
	1,41 1,64 1,79 1,89 1,97 2,04 2,10 2,15	1,41 1,69 1,87 2,00 2,09 2,17 2,24 2,29

Статистическая обработка результатов наблюдений и сравнение экспериментальных данных

При обработке результатов измерений предлагается следующий порядок операций. Для прямых измерений:

- результаты каждого измерения записываются в таблицу (см. стр. 37);

- вычисляется среднее значение из п измерений

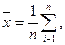
- определяется среднее квадратичное отклонение результата серии измерений

- задается значение надежности;

- исключаются очень грубые результаты измерений (если таковые имеются) по 1_ЛЛ - критерию (см. табл. 2)

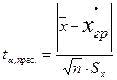
при 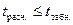результат не считается грубым; при результат исключают из расчетов и заново определяют х и S . Далее определяется коэффициент Стьюдента для заданной надежности 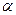и числа произведенных или уточненных измерений п (см. табл. 1, при 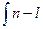);находятся границы доверительного интервала (погрешность результата измерений) .

Если величина погрешности результата измерений (определяемая в предыдущем пункте) окажется сравниваемой с величиной погрешности прибора, то в качестве границы доверительного интервала берется величина

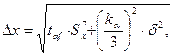
где - величина погрешности прибора;

Окончательный результат записывается в виде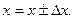

Относительная погрешность результата серии измерений оценивается по формуле:

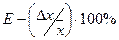
Для косвенных измерений предлагается следующая последовательность вычислений:

- для каждой серии измерений, входящих в определение искомой величины, проводится обработка, как описано выше. При этом для всех измеряемых величин задают одно и то же значение надежности ;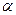

- находится выражение для абсолютной и относительной погрешностей искомой величины в соответствии с конкретным видом функциональной зависимости;

- оцениваются границы доверительного интервала для результата измерений

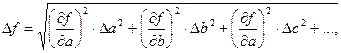
где производные 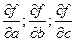вычисляются при …;

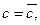- записывается окончательный результат в виде выражений

- определяется относительная погрешность результата серии косвенных измерений

Для сравнения между собой двух средних результатов измерений, полученных в сериях испытаний с разными условиями, применяется - критерий. Такой метод используется, когда необходимо оценить - есть ли влияние вновь выявленного или используемого фактора на искомую величину. Пусть 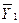получено при из условия 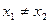. Предположим, что 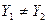. Тогда можно записать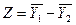

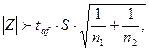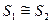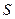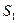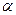Если , то различие между и следует считать существенным и фактор также оказывает влияние на величину . В данном случае предполагается, что и является усредненным значением из и . Значение - критерия выбирается по данным из табл. 1 при заданном и 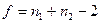(число степеней свободы).