Уравнение состояния идеального газа. Газовые законы.

4.1. Основные понятия и закономерности.

Еще философы древности догадывались о том, что теплота - это вид внутреннего движения. Но только в 18 веке начала развиваться молекулярно-кинетическая теория (МКТ). Цель МКТ - объяснение свойств макроскопических тел и тепловых процессов, протекающих в них, на основе представлений о том, что все тела состоят из отдельных, беспорядочно движущихся частиц. В основе МКТ строения вещества лежат три утверждения:

- вещество состоит из частиц;

- эти частицы беспорядочно движутся;

- частицы взаимодействуют друг с другом.

Качественное объяснение основных свойств газов на основе МКТ не является особенно сложным. Однако теория, устанавливающая количественные связи между измеряемыми на опыте величинами и свойствами самих молекул, их числом и скоростью, весьма сложна. Вместо реального газа, между молекулами которого действуют сложные силы взаимодействия, мы будем рассматривать его физическую модель. Эта модель называется идеальным газом.

Идеальный газ - это газ, взаимодействие, между молекулами которого пренебрежимо мало и молекулы не занимают объема.

Для описания процессов в газах и других макроскопических телах нет необходимости всё время обращаться к МКТ. Величины, характеризующие состояние макроскопических тел без учета молекулярного строения тел называют макроскопическими параметрами. Это объем, давление и температура. Уравнение, связывающее все три макроскопических параметра вместе, называют уравнением состояния идеального газа. Оно имеет еще одно название - уравнение Менделеева - Клапейрона. Получим его:

, , ,

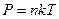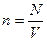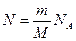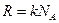
Можно заметить, что это уравнение получено для газа любой массы. Для газа неизменной массы эту зависимость можно представить в следующем виде:

, ,

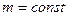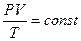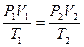
Это уравнение получило название - уравнение Клапейрона. Как можно заметить уравнение Клапейрона является частным случаем уравнения состояния идеального газа.

C помощью уравнения состояния идеального газа можно исследовать процессы, в которых масса газа и один из трех макроскопических параметров остаются неизменными. Количественные зависимости между двумя параметрами при фиксированном значении третьего параметра называют газовыми законами. Процессы, протекающие при неизменном значении одного из параметров, называют изопроцессами.

ИЗОТЕРМИЧЕСКИЙ ПРОЦЕСС - процесс изменения состояния термодинамической системы (газ) макроскопических тел при постоянной температуре называют изотермическим.

В частом случае этого явления, когда масса газа не изменяется, получается газовый закон, носящий имя закона Бойля-Мариотта. Для газа данной массы произведение давления газа на его объём постоянно, если температура газа не меняется. Математическая запись закона выглядит так:

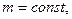
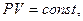
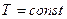
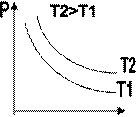
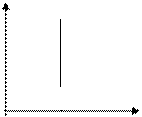
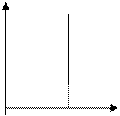
Зависимость макроскопических параметров в различных осях выглядит следующим образом:

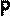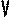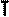Легко заметить, что изотерме располагающейся выше в осях P,V соответствует большая абсолютная температура.

ИЗОБАРНЫЙ ПРОЦЕСС - процесс изменения состояния термодинамической системы (газ) при постоянном давлении называют изобарным.

В частом случае этого явления, когда масса газа не изменяется, получается газовый закон, носящий имя закона Гей-Люссака. Для газа данной массы отношение объёма к температуре постоянно, если давление газа не меняется. Математическая запись закона выглядит так:

, ,

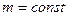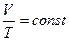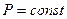
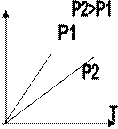
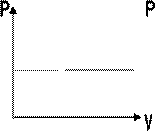
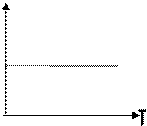
Зависимость макроскопических параметров в различных осях выглядит следующим образом:

Нетрудно определить, что изобаре в осях V,T имеющей меньший угол наклона к оси температур соответствует большее давление.

ИЗОХОРНЫЙ ПРОЦЕСС - процесс изменения состояния термодинамической системы (газ) при постоянном объёме называют изохорным.

В частом случае этого явления, когда масса газа не изменяется, получается газовый закон, носящий имя закона Шарля. Для газа данной массы отношение давления к температуре постоянно, если объём газа не меняется. Математическая запись закона выглядит так:

, ,

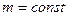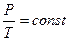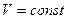
Зависимость макроскопических параметров в различных осях выглядит следующим образом:

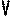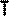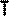Нетрудно определить, что изохоре в осях P,T имеющей меньший угол наклона к оси температур соответствует больший объём.

Решение задач

Зад №1 Какое количество вещества содержится в газе, если при давлении 200кПа и температуре 240К его объем равен 40л?

-? СИ Воспользуемся уравнением состояния идеального газа,

Р=200кПа поскольку в задаче идет речь о состоянии газа.

Т=240к

V=40л Зная, что количество вещества определяется ,

подставим в исходную формулу: , выразим и получим:

ответ: 4 моль

Зад №2 Газ при давлении 0,2МПа и температуре 15⁰С имеет объем 5л. Чему равен объем этой массы газа при нормальных условиях?

СИ Для решения воспользуемся уравнением Клапейрона,

поскольку в задаче речь идет о изменении макропараметров

Р=0,2Мпа без изменении массы газа.

Выразим из уравнения Клапейрона:

Ответ: 9,5л

Зад №3 Как изменился объем газа, если его температура увеличилась в 2 раза, давление возросло на ¼. Первоначальное давление 0,2МПа.

Для решения воспользуемся уравнением Клапейрона, поскольку в

задаче речь идет о изменении макропараметров без изменения массы газа.

Р=0,2Мпа

Учитывая, что давление возросло, то и подставим

в (*), получим:

m=const

Ответ: увеличилось в 1,6 раза

Зад №4 Газ был изотермически сжат с 8л до 5л. При этом давление возросло на 60кПа. Найти первоначальное давление газа.

СИ Воспользуемся законом Бойля-Мариотта, так как в задаче

идет речь о изотермическом процессе без изменения массы

газа.

Так как то имеем

Выразим из предыдущего выражения, получим:

Ответ:

Зад №5 Какой объем займет газ при 77⁰С, если при 27⁰С его объем был 6л?

V₂ - ? В данной задаче переводить литры в м³ нет необходимости, так как воспользуемся законом Гей-Люссака (давление постоянно).

V₁=6л

t₁=27⁰C

t2 = 77⁰C выразим из этого выражения V₂ ,

T₁=300K

T₂=350K

Вычислим:

Ответ: 7л

Зад №6 При какой температуре находился газ в закрытом сосуде, если при нагревании его на 140К давление возросло в 1,5 раза?

Т₀-? Так как сосуд закрыт, следовательно, масса газа не изменятся и объем газа не изменен.

Значит, воспользуемся законом Шарля.

, но и

Следовательно, , на Р₀ можно сократить и преобразовать выражение: Перенесем в левую часть все Т₀ , а в правую все остальное .

Ответ: 280К

Задания на чтение графиков изменения состояния газа при фазовых переходах.

Алгоритм выполнения

1. Определить фазовые переходы состояния газа (изотермический, изобарный, изохорный процессы). Записать анализ ниже предложенного графика.

2. Установить на каждом переходе изменения макроскопических параметров (увеличиваются или уменьшаются).

3. Учитывая графики изопроцессов в различных осях координат (см. ранее), построить графики изменения состояния газа в недостающих координатах.