Теория мономолекулярной адсорбции Ленгмюра. Уравнение Ленгмюра

Изучая адсорбцию на твердых поверхностях Ленгмюр предложил теорию мономолекулярной адсорбции и уравнение адсорбции.

Основные положения теории Ленгмюра следующие:

1. Адсорбция молекул происходит не на всей поверхности адсорбента, а только на адсорбционных центрах, где имеются участки с наиболее нескомпенсированными силовыми полями;

2. Каждый адсорбционный центр может удерживать только одну молекулу адсорбата, при этом адсорбированные молекулы не взаимодействуют со свободными молекулами, что приводит к образованию мономолекулярного слоя поглощаемого вещества;

3. Процесс адсорбции обратим и носит динамический характер, т.к. адсорбированные молекулы удерживаются адсорбционными центрами только в течение определенного промежутка времени, после чего происходит десорбция этих молекул и адсорбция такого же числа новых молекул.

Исходя из этих положений, Ленгмюр предложил уравнение адсорбции:

Г =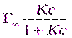

Где Г_∞- значение предельной адсорбции; с – равновесная концентрация адсорбента в системе; К – константа адсорбционного равновесия.

Зависимость адсорбции от концентрации ПАВ (изотерма адсорбции) имеет вид:

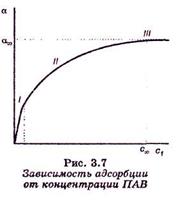
На кривой четко видны три участка:

I - ый участок – это прямая линия, выходящая из начала координат. Действительно, при малых концентрациях, когда с → 0 и (1 + Кс) ≈1, уравнение принимает вид Г = Г_∞·Кс, т.е. величина адсорбции прямо пропорциональна концентрации или давлению адсорбата.

III – участок – соответствует прямой, параллельной оси абсцисс, что означает, что адсорбция достигла своего предельного значения. При этом Кс ›› 1 и (1 + Кс) ≈ Кс, тогда Г = Г_∞ (произошло насыщение поверхности адсорбента молекулами адсорбата, так как сформировался мономолекулярный слой).

II – ой участок соответствует криволинейной части графика и описывается полным уравнением Ленгмюра.

Уравнение Фрёйндлиха

Существует еще одно уравнение, описывающее изотерму адсорбции, называемое уравнением Г. Фрёйндлиха(1906):

А= kС^1/nилиА= kp^1/n

где k и 1/n – константы. (Константа, являющаяся показателем степени, обычно записывается в виде 1/n, а не n, чтобы подчеркнуть, что равновесная концентрация или равновесное давление возводится в степень, которая всегда бывает меньше единицы).

Уравнение Фрёйндлиха является эмпирическим, т. е. за ним не стоит строгой теории. Оно было выбрано среди других уравнений как уравнение параболы, по виду напоминающей изотерму адсорбции. Поэтому теоретическая изотерма, построенная с его помощью, совпадает с экспериментальной только в области средних концентраций. В области же малых и, в особенности, очень больших концентраций (давлений) наблюдаются значительные расхождения между экспериментом и теоретически предсказанными величинами адсорбции. Однако в практической деятельности редко приходится иметь дело с такими областями концентраций. Поэтому уравнение Фрёйндлиха в силу его простоты и лёгкости определения констант, используется очень широко. Особенно часто его используют при исследовании адсорбции на пористых и порошкообразных адсорбентах.

Уравнение Фрейндлиха линеаризуется с помощью логарифмирования:

lgA = lgk + 1/nklgC

или . lgA= lgk+1/ nklgp

С учётом этого для графического определения констант по нескольким экспериментальным данным строится логарифмическая изотерма адсорбции в координатах lgA - lgC или, соответственно lgA - lgр(рис.). В этом случае график при экстраполяции отсекает от оси ординат отрезок ОМ, равный lgk (т. е. k = 100М), а тангенс угла наклона его к оси абсцисс равен 1/n.

Рисунок – Графическое определение констант уравнения Фрёйндлиха