Задача видобутку корисної копалини

Нехай є два родовища А та В корисної копалини, запаси якої відповідно дорівнюють х та у од. Для видобутку копалини використовується одна машина, що або з визначеною можливістю добуває частину золота, або виходить із ладу і надалі не використовується. Якщо машина працює на родовищі А, то з можливістю Р₁ вона добуває частину r, наявного запасу і з можливістю 1-Р₁ виходить із ладу. Якщо на родовищі В, то відповідні дані Р₂; r₂; 1-P₂.

У якій послідовності варто використовувати машину на родовищах, щоб загальна кількість корисної копалини, добутої до виходу машини з ладу, була максимальною?

Рішення: Розіб'ємо період роботи машини на етапи. Процес використання машини можна почати або з родовища А, або з родовища В. Якщо машина не вийшла з ладу на попередньому етапі, то необхідно вирішити, на якому з родовищ її варто використовувати на наступному етапі.

Нехай f_N(x;y) очікувана кількість корисної копалини, добутої до виходу машини з ладу.

Для одноетапного процесу f₁(x;y) = max {p₁r₁x; p₂r₂y} (1.32).

Для N+1 етапного процесу очікувана кількість копалини при початковому виборі родовище

А — f_А(x;y) = p₁[r₁x + f_N(1-r₁)] (1.33)

В — f_В(x;y) = p₂[r₂x + f_N(1-r₂)] (1.34)

Тоді основне функціональне рівняння для N-1 - етапного процесу

f_N-1(x;y)=max[f_A(x;y), f_B(x;y)] = max 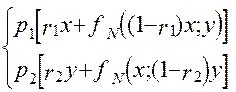(1.35)

Використовуючи функціональні рівняння (1.32); (1.35) визначимо оптимальне поводження в трьох етапному процесі, якщо х=400; у=200; р₁ = 0,7; r₁ = 0,6; p₂ = 0,8; r₂ = 0,8.

Рішення. З (4.32) випливає, що роботу потрібно починати з родовища А, при цьому f₁(x;y) = 0,7*0,6*400 = 168 од.

На початку 2-го етапу робимо вибір: продовжуємо роботу на родовищі А або почнемо на В, з урахуванням того, що на А залишилося (1-r₁)х копалини

f₁[(1-r_A) x;y]= max 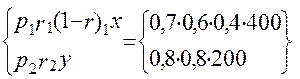= 128 од.

Отже, на 2-ому етапі машина повинна працювати на 2-ому родовищі.

На 3-му етапі вирішуємо використовувати машину на А або В з урахуванням кількості , що залишилася , корисної копалини

f₁[(1-r_A)x; (1-r₂)y] = max 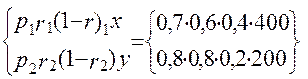= = 67,2од.

Отже, на 3-му етапі машина повинна працювати на А. Таким чином, якщо на 1-ому етапі робота почата на А, то оптимальне поводження: 2-ой етап - У, 3-ий етап - А.

Нехай робота розпочата на В. Тоді на 1-ому етапі

f₁(x;y) = p₂r₂y = 0,8*0,8*200= 128 од.

На початку 2-го етапу робимо вибір

f₁[x (1-r₂);y]= max 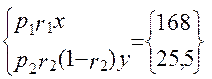= 168 од.

т.ч. роботу варто починати на А на 2-ому етапі.

На початку 3-го етапу

f₁[(1-r₁)х; (1-r₂)y] = max 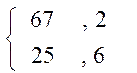= 67,2од.

т.ч. роботу варто продовжувати на А.

Т.ч., якщо на 1-ому етапі робота розпочата на В, то оптимальне поводження: А - на 2-ому і 3-му етапах.

Розглянемо двохетапний і трьох етапний процеси.

Вважаючи N = 1; 2 із (4.35) визначаємо вид функцій, необхідних для рішення задачі.

При N =1 f₂ (x;y] = max 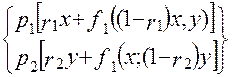(1.36)

При N =2 f₃ (x;y] = max 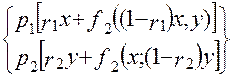(1.37)

де f₂ ((1-r₁) x;y] = max 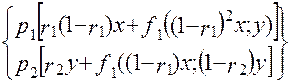(1.38)

f₂ (x; (1-r₁)y) = max 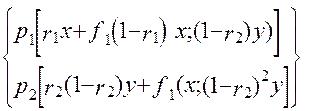(1.39)

Для визначення f₂ необхідно обчислити.

f₁[(1-r₂)² х;y] = max 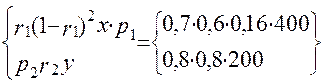= 128 од.

Якщо 1-ий і 2-ий етап експлуатації А, а 3-й етап родовища В.

f₁[х; (1-r₂)² y] = max 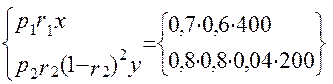=1628 од.

Підставляючи знайдені значення функцій у рівняння (1.36) - (1.39) одержимо для 2-х етапного процесу

f₂ (x;y] = max 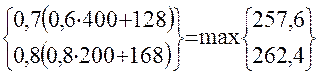=262,4 од.

f₂((1-r₁)(x;y]=max 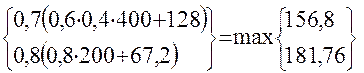=181,7од

f₂ (x₁(1-r₂)y]= max 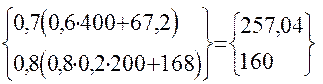= 215,04 од.

т.ч. роботу на 1-ому етапі треба починати на родовищі

В. Для 3-х етапного процесу

f₂ (x;y] = max 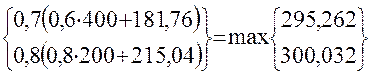= = 300,032од.

т.ч. роботу на 1-ому етапі треба починати на В.

Таким чином, щоб у 3-х етапному процесі добути максимальну кількість корисної копалини (300,032 од) необхідно: 1-ий етап розробляти В, 2-ий і 3-й етапи - родовище А.

До стохастичних відносяться також такі задачі:

1) планування виробництва з урахуванням попиту і споживання;

2) керування запасами;

3) комплектування верстатного парку, якщо замовлення заздалегідь невідомі;

4) планування з/х виробництва і врожайності культур на різноманітних ділянках;

5) планування розвитку транспорту, пасажирських і вантажних перевезень і т.д.