ГЛАВА III. Символ и соседние с ним структурно-семантические категории 4 страница
Всякий миф является символом уже потому, что он мыслит себе общую идею в виде живого существа, а живое существо всегда бесконечно по своим возможностям. Но отнюдь не всякий символ есть миф. Художественные образы в значительной мере символичны, но мифами они являются сравнительно редко.
Надо отдавать себе ясный отчет в том, что всякий миф есть символ, но не всякий символ есть миф Как мы только что сказали, миф есть субстанциальное и вполне буквальное, ни в каком смысле не переносное осуществление, или овеществление, той или иной родовой общности, той или иной общей идеи с обязательным представлением всех этих овеществленных частностей или единичностей в виде живого существа. Но ведь мифическое живое существо только в очень редких случаях мыслится ограниченным какими-нибудь условиями пространства и времени и только в редчайших случаях мыслится смертным. Какого бы мелкого демона в античной мифологии мы ни взяли, об его смертности почти никогда не говорится. Но если мифическое живое существо бессмертно, оно уже по одному этому обладает бесконечными жизненными возможностями, хотя уже и обыкновенное живое существо, несмотря на свою смертность, тоже обладает бесконечными возможностями. В мифе, таким образом, содержится модель для бесконечного ряда предприятий, подвигов, удач или неудач, действия и бездействия в условиях бесконечного разнообразия, в отношениях к окружающему миру. Однако это значит, что всякий миф есть, в нашем смысле слова, символ. Он — модель бесконечных порождений, субстанционально тождественных с самой моделью.
Но можно ли сказать то же самое о символе, то есть можно ли сказать, что он всегда есть тоже миф? Этого никак нельзя сказать, потому что символическая модель не обязательно порождает живые существа с бесконечными жизненными возможностями. Единственно, что можно здесь сказать, это то, что к символической модели часто неприменимы категории времени и пространства. Математическая функция разлагается в бесконечный ряд вне всяких наших представлений о времени и пространстве. Но все же ни сама функция ничего не говорит о своем живом существовании, ни отдельные члены порожденного ею бесконечного ряда. С другой стороны, однако, делается понятным, почему конкретные символы в литературе и искусстве часто тяготеют именно к мифу. Ведь именно миф, состоящий из бесконечных и бессмертных живых существ, наиболее легко поддается символической обработке. И во(145)обще, несмотря на всю идеальную точность математического символа, именно фантастические произведения искусства больше всего пользуются как раз символами. Ведь человеческая фантазия может любые несравнимые и несоизмеримые элементы действительности поставить в закономерный и непреложный ряд. И этот ряд подчинить какой-нибудь еще небывалой модели. Поэтому-то сторонники реалистического искусства и не любят понятия символа. Для них он почти всегда есть нечто фантастическое или, по крайней мере, таинственное. Однако мы должны сказать, что если уж зашла речь о подлинном реализме, то для нас фантастичнее всего сама же человеческая жизнь. И все-таки методы символически-мифологического мышления с познавательной точки зрения оказываются необходимыми в изображении даже максимально прозаических и позитивных сторон жизни, не говоря о прочих ее сторонах. Итак, всякий миф есть символ, но не всякий символ есть миф. Этот миф может изображаться с бесконечно разнообразной интенсивностью своей символики, и символ в конкретных произведениях науки и искусства может как угодно близко подходить к мифу и даже сливаться с ним.
12. Символ и понятие. Наконец, надо уметь ясно формулировать также и то, что, казалось бы, разумеется само собой, но что все-таки не мешает отметить ради ясности мысли. Во всех рассмотренных нами конструкциях фигурируют такие элементы, как идея и образ. Казалось бы, если идея и образ входят в само определение понятия символа, то тем самым отпадает и всякий повод отождествлять с ними символы, поскольку они суть только элементы понятия символа, а не само понятие в целом. Дело, однако, вовсе не так просто, особенно в отношении «идеи».
Даже если не говорить о тех системах идеализма, где идея вполне сознательно и намеренно трактуется как символ, а оставаться только в пределах обычных научных понятий, то, несомненно, и во всяком научном понятии есть нечто символическое. Ведь понятие есть отражение действительности с известной ее переработкой, и прежде всего с ее обобщением. Это общее понятие обладает рядом отдельных признаков, из которых ни один не есть все данное понятие. Разве здесь нет обозначающего и обозначаемого? Обозначаемое здесь, конечно, есть само понятие, а его признаки есть то, что его обозначает. Следовательно, известного рода символическим характером отличается уже само содержание всякого научного понятия. Кроме того, наиболее совершенные научные понятия тоже являются принципом бесконечного ряда подпадающих под него явлений, и общее есть закон появления всего относящегося сюда единичного. Следовательно, не только содержание научного понятия, но и его функционирование среди других понятий, подпадающих под него, тоже символично. В чем же дело? (146) А дело в том, что научное понятие принципиально лишено всякой образности. И если элементы такой образности и трактуются как характерные для какого-нибудь понятия, то, значит, это понятие еще не вполне общее, то есть не вполне совершенное. Итак, символ отличается от понятия тем, что содержит в себе образный элемент, которого нет в научно-выработанном понятии. С другой стороны, и один образный элемент, лишенный всякого понятия, тоже не есть символ. Та конструкция сознания, которая не выходит за пределы непосредственной образности и тем самым исключает всякое самостоятельное понятие, которое в этой образности осуществлялось бы, есть не символ, но натуралистическая копия. Кажется, тут спорить не о чем.
Здесь, может быть, стоит сделать некоторые пояснения к употребленному у нас термину «образ». Термин этот, взятый сам по себе, очень далек от какой-нибудь ясности и точности и допускает десятки разного рода семантических оттенков. Кроме того, выше нам уже приходилось протестовать против выдвижения в символе момента образности. При этом мы аргументировали, между прочим, и тем, что имеются символы и без всякой образности, каковы, например, математические символы. Следовательно, от нас требуется здесь небольшое разъяснение. Может быть, предмет этот станет -яснее, если мы вместо расплывчатого термина «образ» употребим другую, более точную терминологию.
Для этого необходимо отдавать себе отчет в том, что современная наука понимает под «понятием». Здесь, как и в других областях науки, уже давно миновали времена абстрактной метафизики, с точки зрения которой получалось так, что понятие, чем оно больше по объему, тем беднее по своему содержанию. Можно взять понятие «бытие» или понятие «нечто»; с точки зрения школьной логики это будут самые широкие понятия, потому что под них подойдет все существующее, и это будут самые бедные понятия по своему содержанию, в то время как термины «кошка» или «собака» или даже «клоп» обладают огромным количеством разных признаков и потому неизмеримо богаче по своему содержанию по сравнению с «бытием» и «нечто».
Мы не будем здесь опровергать подобного рода давно устаревшую логическую теорию. Мы укажем только на то, что чем наука точнее, тем она дальше отходит от такого противопоставления объема и содержания понятия. Математическая, общность такова, что она вовсе не является пустой абстракцией от единичностей, которые якобы и являются чем-то наиболее конкретным. Подлинное научное понятие таково, что чем оно более общо, тем оно и более конкретно, тем оно более содержит в себе возможности распознать конкретное. Общность для нас не только не содержит в себе все подпадающие под нее (147) единичности, но она является даже, больше того, именно законом получения всех этих единичностей.
Если в математике мы имеем общую формулу для всех кривых второго порядка, то круг, эллипс, парабола и гипербола получаются из этого общего уравнения только путем изменения одного из параметров, входящих в это уравнение. Уравнение кривых второго порядка есть их максимальная общность, но она в то же самое время содержит в себе и закон для получения всех отдельных и единичных кривых второго порядка.
Поэтому, чтобы не сбиться с верного пути, необходимо думать, что понятие отличается от символа вовсе не тем, что оно более общее и более абстрактное, а символ — менее общее и более конкретное. Разумеется, мы имеем в виду максимально совершенные научные понятия, как они выступают в математике и в математическом естествознании. Если мы говорили выше, что символ вещи есть такая ее функция, которая способна разлагаться в бесконечный ряд, то совершенно то же самое мы должны сказать и о понятии, повторяем, если понимать под понятием не какую-нибудь размазанную кашицу субъективных представлений и беспомощную, бессодержательную и пустую общность традиционных учебников логики. И если для символа мы постулировали необходимость разложения в бесконечный ряд, то этот же постулат мы должны применить и к учению о понятии. Здесь не только не будет никакой разницы между символом и понятием. Наоборот, логическая безупречность, точность и красота математического представления об общностях, она-то и заставила нас искать подобных же конструкций в эстетике и в логике.
Но тогда чем же в конце концов символ отличается от логически точно разработанного понятия? Очевидно, здесь дело не в той или иной абстрактности или конкретности, не в той или иной общности или единичности, не в той или иной закономерности возникновения единичного из общего и общего из единичного, и не в наличии возможности разлагать в бесконечный ряд мыслимые здесь функции, символы и понятия, и, наконец, не в самой этой функциональности действительного бытия, поскольку и символ и понятие одинаково являются функциями действительности. Нам представляется, что единственный способ противопоставлять символ и понятие определяется только тем, в каком виде даются и представляются обе эти функции действительности, разложенные в бесконечный ряд.
С этим способом, или, лучше сказать, с различием этих способов, мы встречаемся ежеминутно в нашей повседневной жизни Когда нам нужно надеть пальто и выйти из квартиры по определенному адресу, то мы можем не думать ни о самом пальто, ни об этом адресе, ни о нашем выходе из квартиры. Все эти (148) предметы могут даваться сразу и непосредственно, без всякого их определенного анализа и синтеза, просто в виде вещей и процессов как таковых. Другое дело, если я, надевая пальто, обнаружил отсутствие в нем одной или нескольких пуговиц. Тогда я должен войти в рассмотрение уже самого этого единичного предмета, именно пальто, и должен путем соответствующих мероприятий устранить те или иные его недостатки. В одном случае предмет дан прямо, сразу, непосредственно, без всякого нашего анализа или синтеза и вообще без всякого нашего размышления. В другом случае предмет, наоборот, специально рассматривается, анализируется на отдельные части, а части эти тоже подвергаются дальнейшему анализу и связываются с другими частями только в результате нашего определенного размышления, сопоставления и объединения. Точно так же процесс нашего чтения или письма только уж очень стародавняя психология понимала в виде следования одной буквы за другой и исключительно в виде их механического соединения как таковых. Ничего подобного не происходит в наших обыкновенных процессах чтения или письма. Читая книгу или записывая что-нибудь на бумаге, мы совершенно не думаем ни о каких буквах. Даже ни о каких отдельных словах не думаем, и когда мы произносим или слушаем связную речь, когда мы играем на инструменте, когда мы видим и слышим игру актеров на сцене, мы не замечаем даже отдельных фраз, отдельных тактов в нотописи и отдельных жестов у актеров Это все сливается в единый и неразделимый поток сознания. Но совсем другое дело, когда мы только еще учимся читать или писать, когда мы еще только учимся брать каждую ноту в отдельности и когда в театральной школе учат употреблять те или иные жесты для выражения тех или иных эмоций.
Другими словами, существует непосредственно-интуитивный способ пользования вещами и существует способ мыслительно-дискурсивный И если мы отдадим себе полный отчет в этих двух способах подачи действительности нашему сознанию, то, как нам кажется, выяснится и полное отличие символа от понятия. Функциональность и отражение действительности, обобщенность единичных явлений, закономерность соотношения общего и единичного и возможность разложения в бесконечные ряды — все это дается в символе непосредственно-интуитивно, в понятии же — мыслительно-дискурсивно. Ни в каких других отношениях нет возможности противопоставлять символ и понятие. Фауст у Гёте есть именно символ бесконечных стремлений человека, оправданных ввиду их наивности, честности и бескорыстного самоотдания общечеловеческим идеалам вплоть до инженерно-строительного искусства, причем оправдание это происходит несмотря ни на какие ошибки, соблазны и даже преступления стремящегося человека. (149) Это есть символ потому, что он дается нам в известной трагедии Гете прямо, непосредственно-интуитивно, в виде множества разных образов и картин. Поэтому здесь именно символ человеческого стремления, но никак не его понятие, для которого все эти образы и картины были бы даже и не нужны. Правда, в эпилоге своего произведения сам Гёте нашел нужным подчеркнуть оправданность человеческих стремлений, и притом — даже перед лицом вечности. Но если бы и не было этого эпилога, мы все равно должны были бы понимать трагедию Гёте как символ оправданности человеческих стремлений. При этом оправданность человеческих стремлений выражена в эпилоге «Фауста» опять-таки не чисто понятийно, но почти исключительно образно и интуитивно.
В результате всей предложенной выше описательной характеристики символа в сравнении с понятием необходимо сказать, что символ является такой оригинальной и вполне самостоятельной идейно-образной конструкцией, которая обладает огромной смысловой силой, насыщенностью, вернее же сказать, смысловой заряженностью или творческой мощью, чтобы без всякого буквального или переносного изображения определенных моментов действительности в свернутом виде создавать перспективу для продолжительного или бесконечного развития, уже в развернутом виде.
Все эти черты совершенно одинаково присутствуют как в символе, так и в научно развитом понятии, но в одном случае непосредственно-интуитивно, а в другом случае мыслительно-дискурсивно. В античности — от Гомера и до позднего неоплатонизма — мы, например, наблюдаем картину разнородных пространств, из которых состоит античный космос. И все эти пространственные картины, взятые сами по себе, конечно, являются пока еще только символом. Если же угодно эту систему космических пространств формулировать понятийно, то для этого, во-первых, необходимо будет привлечь и все философские теории досократиков, Платона, Аристотеля, стоиков, эпикурейцев, Плотина и Прокла. Но для настоящей понятийности и всего этого будет мало. Еще надо будет применить методы нашей современной математики и механики, чтобы вместо картинного символа появилась дискурсивная и научная, то есть в подлинном смысле понятийная, характеристика античных типов неоднородного пространства.
13. Диалектически становящаяся картина всех сопоставленных выше структурно-семантических категорий. До сих пор мы попарно сопоставляли символ с разными другими структурно-семантическими категориями. Сейчас, в заключение этого анализа, не худо будет отдать себе отчет в том, какую общую систему категорий мы здесь имеем в виду, и если таковая система существует, то нельзя ли к этой системе категорий подойти диалектически? Ведь с точки зрения диалектической логики, да и с точки зрения (150) диалектики всякой логики науки, не существует и не может существовать никакой раз навсегда данной и в существе своем неподвижной таблицы категорий. Западная философия Нового времени всегда любила упражняться в составлении такого рода таблиц, так что без подобных таблиц не обходилась ни одна абстрактная метафизика. Это и значит быть абстрактным метафизиком с применением формальной логики как основного метода — превращать все в неподвижные категории и строить из таких категорий столь же неподвижные таблицы.
Для современного передового мышления совершенно не существует никаких неподвижных категорий. Все категории текут и меняются, и все они находятся в вечном становлении. Но признавать одно вечное становление, то есть вечную непрерывность, и не допускать никаких прерывных точек, разделяющих отдельные области становления, это тоже было бы чистейшей философской фикцией, поскольку чистейший иррационализм тоже непредставим, нереален и тоже является только иллюзией рассудка. Все категории текут и меняются, однако так, что в результате того или иного непрерывного количественного нарастания данной категории мы вдруг путем скачка переходим в совершенно новое качество, когда и рождается безусловно новая категория.
Спросим себя: нельзя ли все изученные нами структурно-семантические категории расположить именно так, то есть не в виде мертвой и абстрактно-классификационной таблицы неподвижных категорий, но так, чтобы все эти категории возникали у нас постепенно, путем непрерывного становления, и в то же самое время путем логических скачков извещая нас о необходимости возникновения той или другой новой категории. Мы можем признать только такие сущности, которые находятся в непрерывном движении, то есть мы признаем только текущие сущности. И тем не менее, пройдя путь диалектического развития этих категорий, мы убеждаемся в том, что этот путь непрерывного развития содержит в себе и отдельные, уже прерывные скачки, которые являются вехами, характеризующими не только пройденный нами путь диалектического развития, но и логическую закономерность этого пути.
Исходя из этого, можно поставить вопрос, как же именно можно было бы распределить изученные у нас структурно-семантические категории в непрерывно становящийся ряд с прерывными скачками от одной категории к другой и в условиях закономерного соотношения всех непрерывных и прерывных моментов?
Нам представляется, что при изучении всех подобного рода категорий возникают прежде всего вопросы общего и частного, (151) или общего и единичного. Известного рода соотношение общего и единичного характерно и для всякой обыкновенной вещи нашего обиходного и обывательского опыта. Но в нашем обыденном опыте мы не подвергаем специальному рассмотрению подобного рода отношения, поскольку они даются сразу и непосредственно, без всякой рефлексии. Что же касается изученных у нас выше структурно-семантических категорий, то в каждой из них как раз и ставился в качестве основного вопрос о том или другом типе соотношения общего и единичного. Мы сейчас и перечислим изученные нами структурно-семантические категории с точки зрения их нарастающей общности, строго следя за тем, как нарастающая общность становится в них все в новое и в новое отношение к подчиненной ей единичности.
1) Аллегория есть формально-логическая общность, не могущая охватить единичное целиком, а допускающая эту единичность только в меру ее формально-логической структуры: стрекоза и муравей не допускаются в басне всерьез, а только в виде частного примера, в виде единичной иллюстрации для общего суждения о необходимости трудолюбия. Общность аллегории бессильна стать принципом для ее картинной стороны, обладающей своим собственным принципом, не тем общим принципом, ради которого создана аллегория. Баснописец вовсе не думает, что животные по-человечески говорят, но этот человеческий разговор животных принимается только в меру формально-логической басенной общности.
2) Схематическое олицетворение (или олицетворение абстрактного понятия) имеет общность сильнее, чем в аллегории, поскольку все единичное в данном случае является целой субстанциализацией общности: Порок, Добродетель, Грех, Удовольствие в средневековых моралите.
3) Тип обладает еще большей общностью в том смысле, что он не просто находится в отчуждении ко всему единичному, как в аллегории-басне, и не просто овеществляет себя в области единичного, не давая этому последнему развернуться свободно, а сковывая его своей абстрактно-понятийной сущностью. Наоборот, общность здесь конкретизируется настолько, что уже допускает известную свободу для развертывания единичных вещей, лиц и событий. Изображение чиновников, купцов и прочих общественно выраженных типов отнюдь не отбрасывает всю привлекаемую здесь единичность, а, наоборот, использует ее для конструирования более конкретной общности. Правда, в типе его общность все же отличается своей формально-логической структурой. Тем самым сословные или профессиональные типы реалистического романа XIX века не обладают такой конкретностью, чтобы содержать в себе достаточно интенсивную обобщенность, которая бы (152) создавала и самый принцип всей этой типологии. Литературные типы сильного мужа и слабохарактерной жены или слабохарактерного мужа и сильной жены, злой мачехи или преследуемого пасынка — все такого рода типовые обобщения, конечно, не только получают много из их единичных изображений, но они исключительно и строятся на обобщении этих единично наблюдаемых явлений. Но, например, тип злой мачехи сам по себе еще не дает структурную модель для тех или иных единичных явлений и не служит их порождающим принципом, их законом. Он является только их формальным обобщением, так как разнообразных проявлений этого типа злой мачехи может быть бесконечное количество, и все они каждый раз будут сконструированы по-своему. Они обобщаются в тип, но этот формально-логический тип отнюдь не является порождающей моделью их структуры.
4) Художественный образ и, в частности, метафора обладают общностью, которая усиливается до того, что составляющие ее единичности, или видовые различия, уже не отбрасываются, как в аллегории и олицетворении, но сохраняются как равноправные, хотя и противоположные, и общность уже не выходит за их пределы, а целиком с ними отождествляется («Море — смеялось»). Поэтому метафора, признанная разъяснить данную вещь, лицо или событие, резко отличается и от типа, в котором общность возникает только в результате формально-логического обобщения, а не так, чтобы все обобщаемое тут же и присутствовало в обобщенном. Сам Хлестаков не присутствует в типе ревизора, потому что разнообразных ревизоров может быть бесконечное количество. Но если поэт сказал: «Мы — два в ночи летящих метеора», то «мы» и «метеор» есть две такие единичности, которые вовсе не являются обобщением друг друга, но они, хотя и противоположные, сами обобщаются в чем-то третьем, что и делает эти зрительные образы обычно свойственной им единичности художественной общностью, которая и оказалась порождающей моделью для данной метафоры. Правда, чем именно является эта общность в метафоре как таковой, еще не сказано и она еще не подвергнута рефлексии. Моделирующе-обобщающая функция такой художественной образности находит для себя специальное выражение только в символе.
5) В символе общность достигает такой силы, что не просто допускает рядом с собой что-нибудь единичное, отождествляясь с ним (как в художественном образе или метафоре), но является еще и законом, порождающим модные конструирования всех подпадающих под эту общность единичностей; притом таких единичностей может быть целая бесконечность (фигура Медного всадника у Пушкина потому есть символ, что он предполагает бесконечное количество Евгениев, но не Евгениев вообще, как в (153) аллегории, а каждый раз разных Евгениев и каждый раз со своей собственной судьбой, а это значит, что Евгений не является здесь также и только бытовым типом, каковой типизм оторвал бы его фигуру от мощной символики Медного всадника, созданной для изображения возвышенно-трагических судеб новой России, которую Петр I «поднял на дыбы»). При этом общее и единичное в символе и все происходящие между ними процессы имеют структурное, а не субстанциальное значение, как это будет в мифе.
6) Эмблема есть символ специального назначения и потому обладающий характером условности, или конвенционности. Эмблемы государств, классов, сословий, корпораций, профессий, родов и племен, вплоть до чисто личной эмблематики,— все такого рода эмблемы являются в смысле соотношения в них общего и единичного не чем иным, как именно символами, но только — более специального назначения.
7) Миф есть вещественно-данный символ, субстанциализация символа. Это значит, что и принцип конструирования единичностей и сама бесконечность существуют в мифе вполне реально и материально, вполне вещественно и, вообще говоря, вполне субстанциально. Отсюда принцип первобытного мышления — все во всем, а основной закон такого мышления есть оборотничество, то есть возможность превращения всего во все.
В таком примерно виде можно было бы представить себе диалектическое становление изученных у нас структурно-семантических категорий. (154)
ГЛАВА IV Типы символов
В предыдущем мы пытались установить основные элементы понятия символа, тщательно стараясь не путать этого понятия с другими, соседними с ним или очень близкими к нему, часто даже скрепленными с ним, особенно если иметь в виду обывательскую и общелитературную речь. Мы убедились, что большая сложность проблемы приводит здесь к такой путанице терминов, которая является вполне естественной и об устранении которой заставляет думать только очень упорное и очень цепкое функционирование термина «символ», ясно свидетельствующее об его специфичности, пусть хотя бы и бессознательной. Теперь нам предстоит не просто заниматься установлением элементов понятия, но и соотношением разных символов между собой, которые, как показывает исследование, не только разнообразны и прихотливы, но, прямо можно сказать, необозримы. Везде в этих типах будет сохраняться основная особенность символа, сводящаяся к указанию на неизвестные предметы путем какой-нибудь ясной и вполне известной конструкции. Но эта основная особенность символа везде разная в зависимости от тех областей, где символ функционирует. Рассматривая символ в той или иной области познания или действительности, мы замечаем, что, однажды его установив, мы тут же видим и все последствия, которые отсюда происходят. Поэтому в противоположность непосредственному описанию элементов понятия символа мы теперь изучаем те смысловые последовательности, которые возникают при функционировании символа в разных областях и есть не что иное, как учение о типах символов.
1. Научные символы. Уже элементарный логический анализ всякого научного построения с полной убедительностью свидетельствует о том, что он никак не может обойтись без символических понятий. Самая точная из наук, математика, дает наиболее совершенные образы символа. Отрезок прямой только людям невежественным в математике представляется в виде какой-то палочки определенной длины с возможностью делить ее на известное количество частей. На самом же деле, поскольку множество всех действительных чисел, согласно основному учению матема(155)тики, .обладает мощностью континуума и поскольку отрезок прямой содержит в себе именно множество точек, соответствующее множеству всех действительных чисел, необходимо признать, что конечный отрезок прямой в таком понимании является символом получения множества всех действительных (то есть всех рациональных и всех иррациональных) чисел, или, вернее, одним из символов бесконечности.
Уже всякое рациональное число в арифметике только при грубом употреблении его в качестве орудия счета не обнаруживает своего символического функционирования. Теоретически и научно всякое число даже просто натурального ряда предполагает целую бесконечность дробей, отделяющих его от соседнего числа. Всякие иррациональные числа вроде 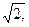
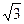 ,
, 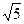 — тоже есть символы в нашем смысле слова, поскольку всякое иррациональное число есть только известный метод порождения бесчисленного количества десятичных знаков. Всякая функция, разлагаемая в бесконечный ряд, тоже есть символ в нашем смысле слова. Ни одна категория математического анализа не обходится без последовательного применения понятия символа. Таковы прежде всего категории дифференциала и интеграла, тоже построенные на получении тех или других величин в результате их непрерывного движения к пределу по определенному закону. В геометрии каждый тип пространства строится тоже по определенному закону, который является для всякого пространства его символом. Таково пространство гиперболическое, параболическое, сферическое.
— тоже есть символы в нашем смысле слова, поскольку всякое иррациональное число есть только известный метод порождения бесчисленного количества десятичных знаков. Всякая функция, разлагаемая в бесконечный ряд, тоже есть символ в нашем смысле слова. Ни одна категория математического анализа не обходится без последовательного применения понятия символа. Таковы прежде всего категории дифференциала и интеграла, тоже построенные на получении тех или других величин в результате их непрерывного движения к пределу по определенному закону. В геометрии каждый тип пространства строится тоже по определенному закону, который является для всякого пространства его символом. Таково пространство гиперболическое, параболическое, сферическое.
Но если зашла речь о геометрии, то для иллюстрации понятия символа вовсе не обязательно оперировать категориями высшей геометрии, и в частности разными типами пространства. Достаточно базироваться уже на элементарной геометрии для того, чтобы не только констатировать наличие здесь символов как бесконечных рядов, но чтобы эти символы даже и представить себе вполне наглядно, вполне, можно сказать, зрительно. Если мы имеем, например, прямоугольный треугольник, то квадрат гипотенузы равняется, как известно, сумме квадратов обоих катетов. Следовательно, если, например, длина каждого катета равняется единице, то гипотенуза будет равняться квадратному корню из двух. Это значит, во-первых, то, что гипотенуза, в нашем смысле слова, есть символ, поскольку она является порождающей моделью для единицы с бесконечным числом десятичных знаков. А во-вторых, эта неисчислимая бездна иррациональности совершенно просто и наглядно видна нашему глазу в виде простой гипотенузы.
