Теорія про мінімакс. усталеність одержуваних рішень

Нехай дана ігрова матриця А={а_ij} та 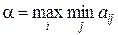, 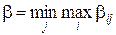. Причому а_ке=α і а_gh=β .

Тоді а_ке≤ а_kh , а а_gh≥а_kh => а_ке=α≤а_kh≤а_gh=β.

Якщо немає сідлової точки (α ¹β), то α <β.

Якщо α <β, то застосування змішаних стратегій S*_А, S*_B повинно призвести до поліпшення в середньому, положення учасників гри, тобто α_А≥ α, α_В≤β, чим при чистих стратегіях.

Як пов'язані α_А и α_В? Відповідь дає теорема про мінімакс.

Теорема У випадку кінцевої антагоністичної гри з повною інформацією α_А=α_В при α ¹ b_.

Ця теорема вказує на існування ситуації рівноваги для випадку α¹b а отже, оптимальних стратегій S*_А, S*_B, тобто рішення гри, що дозволяє домагатися середньоочікуваного виграшу γ=α_А=α_В, називаного ціною гри. Причому α≤γ≤β.

Визначення. Ті з стратегій S_ia, S_jb, що входять до S*_А, S*_B (тобто P_ia>0, P_jb>0) називаються активними стратегіями в складі S*_А, S*_B.

Теорема (про активні стратегії). Якщо один з учасників гри притримується своєї оптимальної змішаної стратегії, то очікуваний виграш залишиться незмінним і рівним γ незалежно від дій іншого учасника в межах його активних стратегій.

Доказ.Нехай J_А, J_B - множина i, j, таких, що P*_ia>0, P*_jb>0, тобто S_ia, S_jb - активні стратегії, γ - ціна гри, при оптимальних S*_А та S*_B, а γ_i - середній виграш А при стратегії S*_А проти S_jb. Очевидно, що γ _i≥ γ (перехід до неоптимальної стратегії S_jb тільки збільшує програш В).

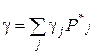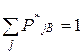Тоді при , де , одержимо, що усі γ_i=γ, тобто програш В не залежить від чистої стратегії S_jb при S*_А. Аналогічний доказ при змішаній стратегії S_b. Тут очікуваний виграш А складе 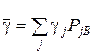, тому що S_b не оптимальний, то 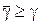, але 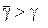, тому що тоді S*_А не оптимальна. Тому 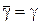. Аналогічно для В.

Зауваження 1. S*_А и S*_B - оптимальні для {а_ij}, оптимальні і для {а_ij+c}.

Висновок. Кожна кінцева (матрична) гра з повною інформацією має хоча б одне рішення або в чистих стратегіях (α=β), або в змішаних (α ¹ β), тобто будь-яка така ситуація має ситуацію рівноваги.

ЗАСОБИ ПОШУКУ ОПТИМАЛЬНИХ СТРАТЕГІЙ.

ЗАГАЛЬНІ ПІДХОДИ

Якщо в матриці А={а_ij} є сідлова точка, то ми маємо а_pq= α = β . Нехай α ¹ β, тобто немає сідлової точки. Тоді рішення треба шукати в змішаних стратегіях S_A={P_1a,P_2a,…,P_ma}; S_B={P_1b,P_2b,…,P_nb}. Так як m і n можуть бути великі, то треба подумати про спрощення гри.

Визначення. Якщо матриця А={а_ij} має властивості а_kj ≥ а_rj (k=1,2, …,m; j=1,2,…,n), k¹r і хоча б одне а_kj>а_rj, то її k-й рядок домінує над r-м рядком.

При а_il≤ а_ih (i=1,2,…,m) і хоча б одному а_il<а_ih , говорять, що l-й стовпчик домінує над h - м. Очевидно сторона А вибере стратегію S_ка, замість S_ra, сторона B - стратегію S_lb, замість S_hb.

Отже при збереженні в матриці А тільки домінуючих рядків і стовпчиків ціна гри не зміниться, але зменшиться її розмірність. Ця властивість гри називається редукцією.

Приклад 3.

	S1b	S2b	S3b	S4b	2-ий стовпчик домінує над 4-м		S1b	S2b	S3b	3-ий рядок домінує над 1-м
S1a					S1a
S1a					S2a
S1a					S3a

	S1b	S2b	S3b	2-ий стовпчик домінує над 3-м		S1b	S2b	Гра зредуциру-вала з 3´4 до 2´2
S2a				S2a
S3a				S3a

Іншим розповсюдженим способом спрощення ігор являється штучна заміна вихідних чистих стратегій S_1a,…,S_ma,S_1b,…,S_nb очевидними змішаними стратегіями з внесенням відповідний коректив у платіжну матрицю А.

Приклад 4. Нехай у грі припускається змішування стратегій у рівних пропорціях. Так в силу однаковості елементів перших двох стовпчиків стратегій S_1b і S_2b потрібно змінювати з частотою ½ (без урахування S_3b і S_4b).

Такою ж властивістю володіє і S_3b та S_4b.

Нові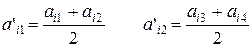

S1b

S2b

S3b

S4b

Þ

S’1b

S2b

S1a домінує над S2a

S’1b

S2b

S1a

S1a

3,5

S1a

3,5

S1a

-7

S2a

-3,5

S2a

-3,5

S1a

-7

-1

-1

S3a

-1

Тоді а₁₁=3,5 - сідлова точка. Отже оптимальне рішення (S_1a, S_1b).

Висновок. При дослідженні будь-якої гри (m´n)

1) перевіряємо, чи є в А сідлові точки і пов'язані з ними рішення в чистих стратегіях;

2) якщо α¹β , то намагаються виявити домінуючу стратегію, а також стратегії, що призводять до однакових результатів;

3) потім переходять до формування змішаних стратегій. У результаті знаходиться спрощена гра без сідлових точок, аналог гри m´n.