Постановки потоковых задач

ЗАДАЧА О МАКСИМАЛЬНОМ ПОТОКЕ

Постановки потоковых задач

Здесь приводится классические и наиболее часто используемые варианты постановки задач теории потоков. Начнем с общей задачи теории потоков.

Пусть G=(V,E) – ориентированный граф, в котором V – множество вершин и E – множество дуг. На множестве дуг графа заданы две функции: c(i,j) – цена дуги (i,j) и u(i,j) – пропускная способность дуги (i,j). Предположим, что паре вершин однозначно соответствует дуга, если она есть. Для каждой вершины iÎV определим величину b_i – потребность в обеспечении. Эта величина показывает, сколько вещества требуется данному стратегическому пункту или сколько вещества в этом пункте в избытке. Если b_i>0, то пункт i называется пунктом производства (вещество в избытке), если b_i<0, то пункт i называется пунктом потребления (вещество в недостатке). Если же b_i=0, то речь идет о транзитном пункте. С этими обозначениями общая задача теории потоков (она же задача поиска потока минимальной стоимости в общем виде, она же – транспортная задача) запишется следующим образом:

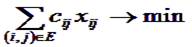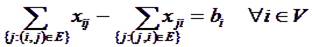Вектор x=(x_ij) называется потоком в сети G. Первое ограничение задачи (уравнения баланса) показывает, что поток, проходящий через вершину, должен оставлять (или забирать) ровно необходимое ей количество вещества. Последнее ограничение запрещает превышение пропускной способности дуг сети. Речь идет о поиске оптимального (в смысле транспортных затрат) способа доставки товара (вещества) из пунктов потребления в пункты производства. Задача не имеет решения, если не выполнено условие баланса

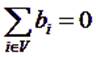однако замкнуть (сбалансировать) задачу можно путем добавления фиктивной вершины, которая будет иметь потенциал, равный

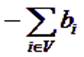Особую роль в теории потоков и в истории ее развития имеют следующие частные случаи модели.

Пусть имеются две особые вершины s,tÎV. Пусть C_jj означает длину дороги из пункта i в пункт j. Требуется найти кратчайший путь из s в t. Для решения задачи о поиске кратчайшего пути, положим в общей модели b_s=1 и b_t=-1, а для остальных вершин iÎV/{s.t} положим b_i=0. Выберем u_ij=1 для всех дуг сети. Решением задачи поиска потока в этом случае будет является кратчайший путь из пункта s в пункт t.

Пусть мы имеем, как и в предыдущем случае две особых вершины: s, которую будем называть истоком, и t, называемую стоком. И мы хотим определить максимальное количество вещества, которое можно перемещать из истока в сток, не превышая пропускных способностей дуг сети и с тем условием, что при перемещении вещество не может накапливаться в вершинах. Для решения этой задачи положим b_i=0 для всех, iÎV,c_ij=0 для всех (i,j)ÎE и введем дополнительную дугу (t,s), для которой положим c_is=-1 и u_is=¥. Такая задача называется задачей поиска максимального потока в сети. Речь идет о том, чтобы найти способ перемещать в единицу времени как можно больше вещества из истока в сток (то же самое, что максимизировать поток, идущий обратно по дуге из t в s).

В 1956 году классическая задача поиска максимального потока была поставлена Фордом и Фалкерсоном и записана уже не в терминах задачи линейного программирования, а в терминах новой теории – теории потоков. Ими же отдельно сформулирована задача поиска максимального потока и предложен первый алгоритм ее решения, не имеющий ничего общего с симплексным методом, которым подобная задача, поставленная в терминах задачи линейного программирования решалась Данцигом.

Кроме задачи поиска максимального потока, рассматривается задача поиска потока минимальной стоимости так же имеющая свои особенности, которые выходят за пределы нашей работы.

Эти задачи – о кратчайшем пути, о максимальном потоке, о потоке минимальной стоимости (транспортная задача) – получили широкое применение в различных областях человеческой деятельности и каждая из них развивалась своим путем. Было разработано множество алгоритмов, которые находят решения потоковых задач в их частных случаях, и каждый новый алгоритм нес в себе идею, которая могла быть применена к каждой вариации общей задачи теории потоков в том или ином виде. Было разработано множество структур данных, которые обобщались и на многие другие задачи и прикладной математики.