Построение трехмерных изображений
Не всегда весь объем визуализируемой информации удобно представить в виде набора двумерных кривых. Иногда, по смыслу задачи, данные должны быть представлены как объекты трехмерного пространства. Для изображения таких объектов рассмотрим несколько функций.
Способ обращения к команде plot3, а также список дополнительных параметров полностью совпадает с описанным в п. 2.5.1 и далее. Аналогично функциям plot( ) - plot3( ) существует пара функция comet( ) - comet3( ). Функция comet3( ) используется так же, как и comet. При использовании для обрисовки трехмерной кривой функции (объекта) line( ) можно обращаться к этой функции как к функции plot( ), т.е. line(x,y,z).
Трехмерные поверхности обычно описываются функцией двух переменных z(x, у).Специфика построения трехмерных графиков ("по точкам") требует не просто задания ряда значений векторов х и у. Она требует определения для X и Y двумерных массивов — матриц, которые используются для дальнейших вычислений и построений трехмерных поверхностей. Для создания таких массивов служит функция meshgrid( ). В основном она используется совместно с функциями построения графиков трехмерных поверхностей.
Функция meshgrid( )записывается в следующих формах:
[X,Y] = meshgrid(x) — аналогична [X,Y] = meshgrid(x,y);
[X,Y,Z] = meshgrid(x,y,z)
и возвращает трехмерные массивы, используемые для вычисления функций трех переменных и построения трехмерных графиков;
[X.Y] = meshgrid(x.y)
преобразует область, заданную векторами х и у, в массивы X и Y, которые могут быть использованы для вычисления функции двух переменных и построения трехмерных графиков. Строки выходного массива X являются копиями вектора X.
| Пример3.2-13 |
| >> [X,Y]=meshgrid(0:3,-3:0); >> X = 0 1 2 3 0 1 2 3 0 1 2 3 0 1 2 3 >> Y = -3 -3 -3 -3 -2 -2 -2 -2 -1 -1 -1 -1 0 0 0 0 >> |
Эти данные используются функциями
mesh(X,Y,Z) – построение сетчатого графика, где X,Y,Z – матрицы одинаковой размерности;
plot3(X,Y,Z) –построение точек, соединенных отрезками прямых (аналог plot); urf(X,Y,Z) –построение поверхности и др.
Кроме численных методов построения можно использовать символьные: ezmesh( ), ezsurf( ), ezplot3( ) и т. п. Синтаксис использования этих функций прост.
Рассмотрим пример 3.2-14 построения графика синуса на интервале от -4 до 4.
| Пример3.2-14 |
| >> ezsurf('sin((x^2+y^2)^(0.5))/((x^2+y^2)^(0.5))',[-10 10],[-10 10]) >> |
Рис. 3.2-16
Заключенное в апострофы – это функция, график которой необходимо построить, в скобках указаны пределы (их можно и не задавать). Обратите внимание на отсутствие . и eps – этого просто не надо.
Кроме этого, эти функции позволяют строить графики, заданные параметрически, задавать различные параметры графиков и другие возможности (посмотрите help).
Трехмерные сеточные поверхности изображаются с помощью функции mesh( ). Команда mesh(z)изображает в трехмерной перспективе поверхность, описываемую элементами матрицы z. Эта поверхность определяется Z-координатами точек над прямоугольной сеткой в X-Y плоскости. Попробуйте выполнить самостоятельно команду mesh(eye(10)). Для того чтобы нарисовать функцию z=f(x,y) над прямоугольником, необходимо определить вектора xx и yy , которые определят разбиение сторон прямоугольника. С помощью команды meshgrid можно создать матрицу x, каждая строка которой будет совпадать с xx, а размер столбцов которой будет совпадать с длиной вектора yy, и, аналогично, матрицу y, каждый столбец которой совпадает с yy, следующим образом [x,y] = meshgrid(xx,yy);. После этого необходимо определить матрицу z, вычисляя каждый ее элемент как функцию f в соответствующих точках, определяемых матрицами x и y, после чего использовать команду mesh.Вы можете, например, нарисовать поверхность на квадрате [-2,2] х [-2,2] с помощью следующего набора команд
| Пример3.2-15 |
| >> xx = -2:.1:2; >> yy = xx; >> [x,y] = meshgrid(xx,yy); >> mesh(z) >> |
Первые три строки можно заменить на [x,y] = meshgrid(-2:.1:2, -2:.1:2); .
Более полно с возможностями изображения трехмерных поверхностей можно познакомиться с помощью оперативной помощи (help plot3/mesh/surf).
Одним из популярных способов визуализации поверхностей является изображение изолиний. MatLab предоставляет возможность построения изолиний двух типов -двумерных или плоских, фактически являющихся проекциями соответствующих линий постоянного значения на плоскость X-Y, и трехмерных изолиний, нарисованных в какой-либо перспективе.
Простейшим способом изобразить изолинии на плоскости – это обратиться к функции contour(Z), где Z -это матрица, содержащая значения исследуемой поверхности на равномерной сетке, т.е. Zij = f(i, j). При таком обращении система MatLab сама выберет число изолиний и значения функции, при которой они будут построены. Если вы хотите сами задать число выводимых изолиний, то необходимо обращение вида contour(Z,n_of_lines), если же необходимо задать сами эти уровни, то это можно сделать с помощью обращения contour(Z,values_of _levels). Если вам необходимо нарисовать одну изолинию с определенным значением функции, то вектор, содержащий уровни, должен иметь два одинаковых элемента, равных этому уровню.
Отмеченные выше три способа вызова функции построения изолиний строят их по отношению к номерам строк и столбцов матрицы Z так, что элемент Z(1,1) будет помещаться в левом нижнем углу рисунка. Можно построить изолинии относительно выбранных вами масштабов по оси X и Y . Для этого необходимо передать функции вектора или матрицу координат, определяющие координаты каждого из элементов матрицы Z. Эта передача осуществляется путем одного из следующих обращений:
| Пример3.2-16 |
| >>contour(x,y,Z); contour(x,y,Z,n_of_lines); >>contour(x,y,Z,values_of_levels); >> |
В трехмерной графике выполняются представления функции z=z(x,y), отличающиеся способом соединения точек: линия, сечения, сетчатая или сплошная поверхность.
plot3(x,y,z) в тех же вариациях, что и plot( ), предполагает задание одномерных и двумерных массивов (строятся точки с координатами x(i,:),y(i,:),z(i,:) для каждого столбца и соединяются прямыми линиями. Если используется [x,y]=meshgrid( ), то строятся сечения.
| Пример3.2-17 | |
| >> t=0:pi/50:10*pi; >> [x,y]=meshgrid([-2:0.1:2],[-2:0.01:2]); | |
| >> plot3(sin(t),cos(t),t) >>z=exp(-x.^2-y.^2); >> plot3(x,y,z) | |
| >> | |
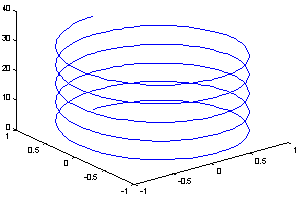 Рис.3.2-24 Рис.3.2-24 |
В примере mesh(x,y,z,c), mesh(z,c), mesh(z) определяют задание сетчатой поверхности (массив с определяет цвета узлов поверхности; если x,y не указаны, то x=1:n, y=1:m, где [m,n]=size(z).
| Пример 3.2-18 |
| >> [x,y]=meshgrid(-8:0.5:8); |
| >> t=sqrt(x.^2+y.^2)+0.001; |
| >> z=sin(t)./t; |
| >> mesh(x,y,z) |
| >> meshc(x,y,z) |
| >> |
Аналогичная функция meshс( ) в дополнение к поверхности строит проекции линий уровня, а meshz( ) делает срез поверхности до нулевого уровня (своеобразный пьедестал).
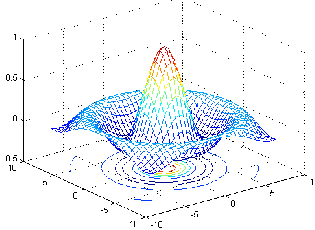 Рис. 3.2-25 Рис. 3.2-25 |
Функции surf(x,y,z,c), surf(z,c), surf(z) определяют задание сплошной поверхности, отличаясь от mesh( ) системой окраски; аналогичная функция surfс( ) задает проекции линий уровня.
Реализация трехмерной графики может сопровождаться множеством вспомогательных команд, например:
· hiddenon/off включает или выключает режим удаления невидимых линий (по умолчанию on);
· shadingfaceted / flat / interp устанавливает затенение поверхностей (по умолчанию faceted дает равномерную окраску ячеек с черными гранями, flat - цветами узлов сетки, interp- интерполяцией цветов.
Создание графического объекта исходит автоматически при обращении к командам, порождающим объекты Line( ) и Surface( ), но может выполняться и командой
axec('<имя свойства>',<значение>, ...).Есть и команды более высокого уровня:
axis([xminxmaxyminymax]),
axis([xminxmaxyminymaxzminzmax]),которые устанавливает масштаб по осям;
axesoff/onвыключает (включает) вывод на координатные оси обозначений и маркеров;
gridon/off, gridвключает (выключает) или переключает режим нанесения координатной сетки на осях;
boxon/off, boxвключает (выключает) или переключает режим рисования контура параллелепипеда, трехмерный объект;
zoomon/offвключает (выключает) режим интерактивного масштабирования графиков (левая мышь около точки увеличивает масштаб вдвое, правая - уменьшает; удержанием левой мыши можно выделить прямоугольную область для детального просмотра;
zoomout восстанавливает исходный график.
В отличие от meshс (...) и surfс(...) функция contour рисует только линии уровня соответствующих поверхностей и выступает в многообразии синтаксических форм: contour(X,Y,Z) - для массива Z =Z(X,Y), contour(X,Y,Z,n) - то же с указанием числа линий уровня (по умолчанию 10), contour(X,Y,Z,v) - то же для массива указанных значений ;contour(Z), contour(Z,n), contour(Z,v) - аналогичные функции без указания диапазонов для аргументов и contour(...,LineSpec) - аналогичные функции c указанием типа и цвета линий (см. plot); [C,h]=contour (...) возвращает массив С и вектор дескрипторов, позволяя тем самым продолжить работу с рисунком (давать оцифровку линий, заголовки и др.).
Функция contourf(...) закрашивает области между линиями уровня, аналогична contourf(...) с разницей в формате[C,h, cf]=contour (...), где cf определяет матрицу раскраски.
Пример 3.2-26 Пример 3.2-27
| >> [x,y]=meshgrid(-8:0.5:8); | >> [x,y]=meshgrid(-2:0.25:2); |
| >> t=sqrt(x.^2+y.^2)+0.001; | >> t=sqrt(x.^2+y.^2)+0.001; |
| >> z=sin(t).^3./t; | >> z=sin(t).^3./t; |
| >> [c,h]=contour(x,y,z,20); >> | >> [c,h,cf]=contourf(x,y,z,4); >> |
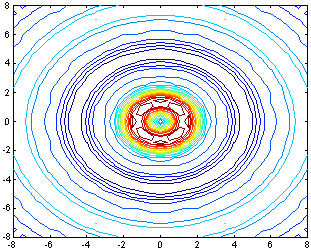 Рис. 3.2.26 Рис. 3.2.26 | 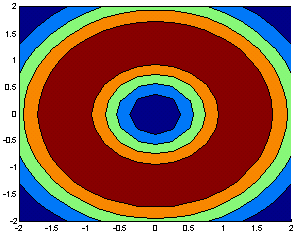 Рис. 3.2.27 Рис. 3.2.27 |
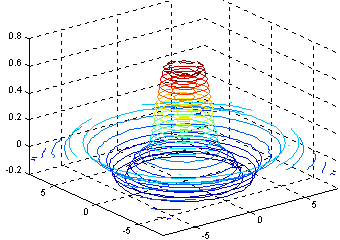 Рис. 3.2.28 Рис. 3.2.28 | Функция contour3(...) по синтаксису полностью аналогична contour(...), но изображает не проекции линий уровня, а рисует их в пространственной интерпретации; так команда [c,h]=contour3(x,y,z,20); дает фигуру (рис. 3.2.28). |
