С.м.о. із відмовами. рівняння ерланга

Мал. 9

Нехай є n-канальна С.М.О. із відмовами. Розглянемо її як фізичну систему S із кінцевою множиною станів S_k, де S_k - зайнято рівно k каналів, k = 0, ... , n

Граф переходів даний на мал. 9.

Визначити ймовірність станів системи P_k(t) (k= 0, ..., n) для будь-якого моменту часу t. Допущення:

1) потік заявок - найпростіший, із щільністю l.

2) час обслуговування Т_об, показове, із параметром

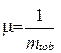g(t) = me-^{m t} (t>0) (2.25)

де m_tоb = M(T_ob) - математичне сподівання.

Величину m можна витлумачувати як (інтенсивність) щільність потоку звільнення зайнятого каналу.

Так як обидва потоки, заявок і звільнень, найпростіші, процес, що протікає в системі є марковським.

Очевидно, що для визначення P(t) можна скористатися математичним апаратом безперервних ланцюгів Маркова.

Для цього знайдемо щільності ймовірностей переходу системи із стану у стан. Перехід системи із стану у стан може трапитися або за рахунок появи заявки або за рахунок обслуговування заявки.

Так як потоки заявок і вивільнення каналів найпростіші, значить ординарні, то за час 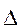t у системі може з'явитися тільки одна заявка і канал може обслугувати лише одну заявку. Позначимо через подію Z - появу заявки, через О - вивільнення в каналах від заявки, за час 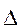t. Для найпростіших потоків із щільністю (інтенсивністю) l, ймовірність появи n подій за час знаходиться за формулою Пуасона.

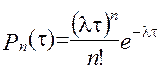(2.26)

Тоді 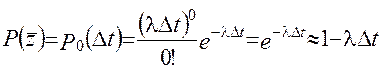(2.27)

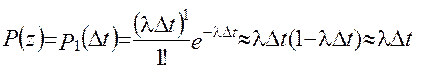(2.28)

З огляду на те, що щільність потоку обслуговування заявок m, аналогічно

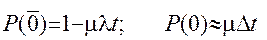(2.29) - (2.30)

Тоді за визначенням щільності ймовірності потоку переходу системи за рахунок надходження заявки

f_заяв(t) = 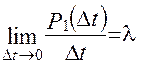(2.31)

Аналогічно одержуємо щільність ймовірності потоку переходу системи за рахунок обслуговування заявки

f_об(t) = 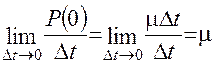(2.32)

Зауваження 3 . Якщо система знаходиться в стані S_k, тобто зайнято k каналів, то ймовірність звільнення одного каналу з k

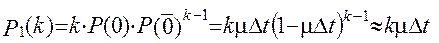
Тоді щільність ймовірності переходу системи із стану S_k у стан S_k-1 буде

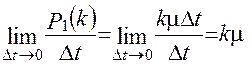(2.33)

Тепер, нанесемо отримані щільності ймовірностей переходу на граф станів і отримаємо розмічений граф станів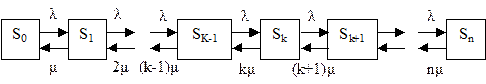, мал.10.

Мал. 10

Складемо для системи як для Н.М.Л. систему диференційованих рівнянь Колмогорова для ймовірностей переходу

P¢₀(t) = -P₀(t) + mP₁(t)

P¢₁(t) = lP₀(t) - (l +m)P₁(t) + 2mP₂(t) (2.34)

--------------------------------------------------

P¢_k(t) = lP_k-1(t) - (l +km)P_k(t) + (k+1)mP_k+1(t)

--------------------------------------------------

P¢_n(t) = lP_n-1(t) - nmP_n(t)

Рівняння (34) називаються рівняннями Ерланга.

Інтегрування системи рівнянь (34) при початкових умовах Р₀(0) = =1; Р₁(0) = ... = P_n(0) = 0, тобто в початковий момент усі канали вільні, дає залежність P_k(t) для будь-якого k.

P_k(t) характеризують середнє завантаження системи і її зміну з часом. Зокрема, P_n(t) є ймовірність того, що заявка, що надійшла в момент t, застане всі канали зайнятими (одержить відмову): Р_від = P_n(t).

Величина g(t) = 1 - P_n(t) називається відносною пропускною спроможністю системи. Для моменту t це є відношення середнього числа обслуговуваних за одиницю часу заявок до середнього числа поданих.

Зауваження 4. При виведенні рівнянь Ерланга ми ніде не користувалися тим, що величини l та m постійні. Тому рівняння (2.34) справедливі і для l(t) і m(t), аби лише потоки в системі були пуасоновськими.