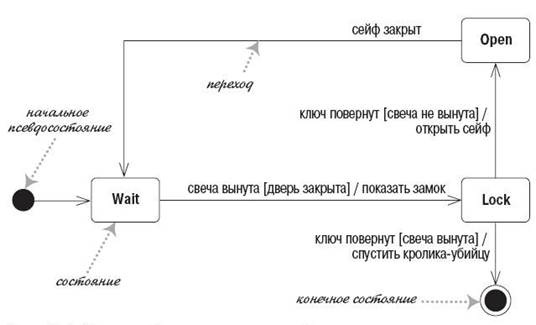
Алгоритм создания диаграммы автомата

Практическая работа №7.

Моделирование поведения: диаграммы автомата.

Цель работы

Цель практической работы – формирование практических навыков разработки диаграммы автомата.

Назначение диаграммы автомата

Диаграммы автоматов (англ. state machine) используются для описания поведения, реализуемого в рамках варианта использования, или поведения экземпляра сущности (класса, объекта, компонента, узла или системы в целом). Поведение моделируется через описание возможных состояний экземпляра сущности и переходов между ними на протяжении его жизненного цикла, начиная от создания и заканчивая уничтожением. Диаграмма автоматов представляет собой связный ориентированный граф, вершинами которого являются состояния, а дуги служат для обозначения переходов из состояния в состояние.

Основные элементы диаграммы автомата

Основными элементами диаграммы автомата являются состояния и переходы. Состояния бывают простыми и составными. Составное состояние делится в свою очередь на составное последовательное и составное ортогональное. Переходы бывают простые, сегментированные и составные. Простые переходы осуществляются по событию или по завершении и всегда ведут из одного исходного состояния в одно целевое состояние. Переходы могут иметь сторожевые условия. Специальными состояниями, разделяющими сегменты сегментированного перехода, могут быть: состояние выбора и переходное состояние, а для составного перехода — развилка и слияние. Кроме названных, к специальным состояниям относятся: начальное, поверхностное и глубинное исторические состояния, состояние прекращения выполнения и заключительное состояние. Дополнительные удобства представляют точки входа и точки выхода, которые применяются на составных и ссылочных состояниях.

Алгоритм создания диаграммы автомата

При разработке диаграмм автоматов следует придерживаться следующих правил и рекомендаций.

1. Наличие у экземпляра сущности нескольких состояний, отличающихся от простой схемы «исправен – неисправен» или «активен – неактивен», служит признаком необходимости построения диаграммы автоматов. При выделении состояний и переходов следует помнить, что длительность срабатывания переходов должна быть существенно меньшей, чем нахождение моделируемого объекта в соответствующих состояниях. Каждое из состояний должно характеризоваться определенной устойчивостью во времени. Так, на рис. 1.1 при моделировании поведения технического устройства, в простейшем случае, можно выделить два или три состояния. При этом в одном случае ремонт показан в качестве перехода, т. е. считается, что занимает мало времени, а в другом – в качестве состояния, что больше соответствует реалиям жизни.

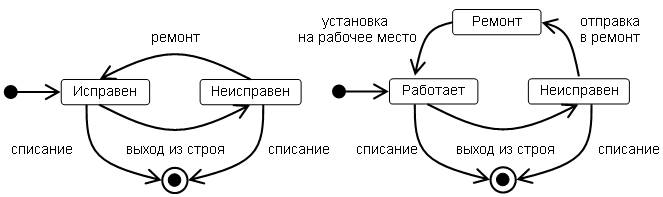
Рис. 1.1 Примеры выделения состояний и переходов

2. Автомат (диаграмма) обязательно должен начинаться знаком начального состояния и заканчиваться знаком конечного. Начальное состояние указывается только один раз, а конечных может быть несколько в целях минимизации пересечений переходов. Для подавтоматов рекомендуется придерживаться этого же правила или использовать точки входа / выхода. Допускается не указывать начальных / конечных состояний и точек входа / выхода для составных состояний или подавтоматов, когда начальное подсостояние (подсостояния) очевидны.

3. Для облегчения восприятия диаграммы рекомендуется использовать декомпозицию со скрытием составных состояний.

4. Диаграмма не должна содержать изолированных состояний и переходов. Переходы и их спецификация должны быть заданы таким образом, чтобы на графе каждое состояние было потенциально достижимо из начального и из любого состояния было потенциально достижимо конечное. На следующем рсунке из состояния 2 нет пути в конечное, а из начального состояния нет пути в состояние 3.

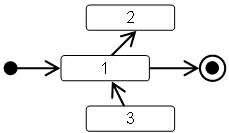
Рис. 1.2 Пример неправильно составленной диаграммы

5. Триггерные переходы по условию на диаграмме можно показать тремя способами.

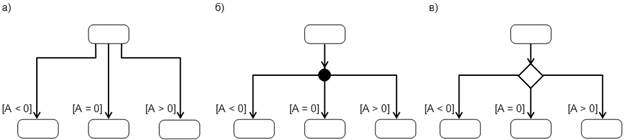
Рис. 1.3 Способы отображения триггерных переходов по условию

6. В каждый момент времени автомат или подавтомат должен находиться только в одном состоянии. Это означает, что спецификация переходов из одного состояния не должна допускать потенциальной возможности перехода в два и более состояний. На следующем рисунке приведены примеры фрагментов диаграмм с конфликтными переходами.

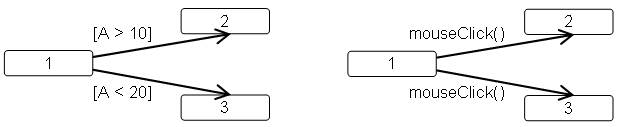
Рис. 1.4 Фрагменты диаграмм с конфликтными переходами

Исключением из этого правила является параллельный переход в подсостояния параллельных подавтоматов одного составного состояния.

Пример

Задание: Создать диаграмму автомата, которая управляет системой безопасности