Лабораторная работа № 1. Простые геометрические тела

Сложные объемно-пространственные композиции состоят, как пра­вило, из простых линейных, плоскостных или объемных элементов. Что касается объемных форм, то для объемной формы (тела) характерно относительное равенство размеров по трем коорди­натам, (измерениям).

Помимо соотношения размеров объемные тела имеют и другие характеристики, такие как характер очертания их поверхности.

По этому признаку можно разделить все объемные тела на четыре группы:

1. Тела, образованные плоскостями, имеющими перпендикулярные ребра (кубы, прямые призмы);

2. Тела, образованные наклонными плоскостями (пирамиды, на­клонные призмы и др.);

3. Тела вращения и формы, образованные криволинейными повер­хностями (сфера, конус, цилиндр и др.);

4. Сложные стереометрические фигуры, имеющие прямолинейные и криволинейные поверхности.

Изучение объемных форм мы начнем с простых геометрических тел, из которых, как из детского конструктора в дальнейшем будем создавать сложные объемно-пространственные композиции.

Правильные многогранники (призмы, пирамиды). Многогранником называется геометрическое тело, ограниченное многогранной поверхностью, состоящей из плоских многоугольников. Каждая сторона многоугольника служит одновременно стороной другого. Сами многоугольники называются гранями, а общие их стороны - ребрами, точки пересечения трех и более ребер - вершины многогранника.

ЗАДАНИЕ 1.Выполнение макетов простых геометрических тел (рис. 1, 2).

Цель:Овладеть первичными моторными на­выками макетирования.

Задачи:Познакомиться с основными на­чальными приемами изготовления макетов объемных форм.

Требования:Выполнить макеты: куба (8x8 см), цилиндра (диаметр 8 см, высота 16 см), пирамиды (сторона 8 см, высота 16см), конуса (диаметр 8 см, высота 16см) по предложенным образцам.

Методические указания:Приведенные на схе­ме развертки куба и пирамиды (рис. 3) скле­иваются встык клеем ПВА. Чтобы линии сгиба на ребрах куба и пирамиды были ров­ными и четкими, необходимо с внешней сто­роны бумаги по линии сгиба сделать надсеч­ку. Надсечка делается на 0,5 толщины листа бумаги, это надо делать легко, чтобы не про­резать бумагу насквозь. Затем нужно согнуть бумагу по этим линиям и склеить стыки. Основания конуса и цилиндра (окружно­сти) вырезаются ножом и подравниваются ножницами. Окружность можно вырезать и при помощи измерителя, если очень хорошо заточить одну из иголок. Для склеивания боковых поверхностей конуса и цилиндра можно предусмотреть дополнительный кла­пан. Чтобы боковая поверхность цилиндра согнулась ровно, можно на ее выкройку на­нести надсечки через равные промежутки (5 мм). Ровную кривизну можно получить также, если скручивать детали между двух листов пленки, используемой для рентге­новских снимков. Для склеивания основа­ния с боковой поверхностью цилиндра, на обоих кругах основания построить отвороты в виде треугольников, затем надрезать отвороты с наружной стороны, загнуть и склеить объем (рис. 1).

Рис. 1

На всех приводимых далее исходных чертежах приняты определенные условные обозначения: самая толстая линия соответ­ствует линии основного контура и прореза­ется насквозь; пунктирная линия — неви­димый контур, ее надо надсечь с изнаноч­ной стороны; самая тонкая линия соответ­ствует надсечке с лицевой стороны.

Чтобы качество макета было высоким, надо сделать очень точный чертеж, сделать надсечки и прорези, а следы карандаша аккуратно стереть. Иногда можно не поль­зоваться карандашом, а делать уколы изме­рителем в нужных местах. Сначала на вы­кройках делаются надсечки, а потом сквоз­ные прорези.

Рис. 2

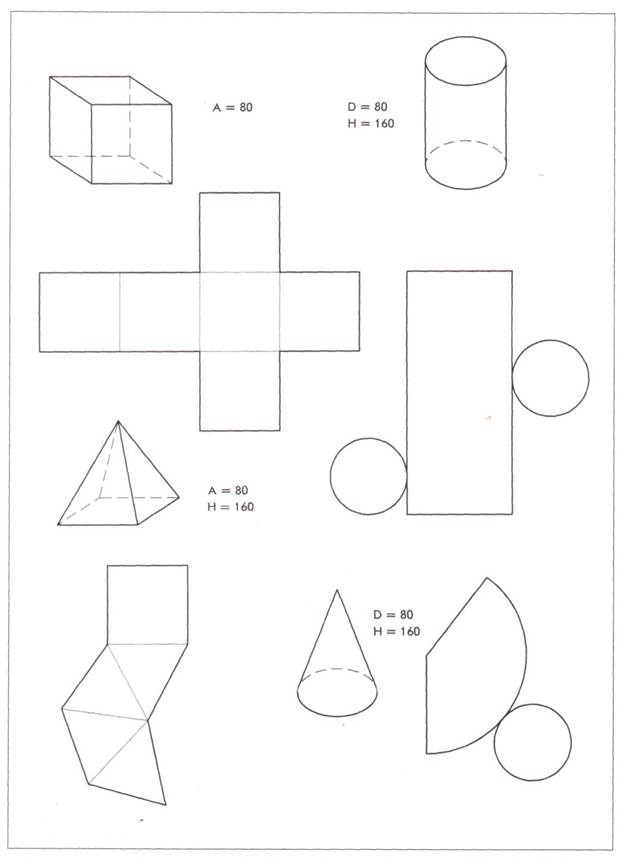
Рис. 3. Развертки куба, цилиндра, пирамиды, конуса