Граничні ймовірності станів для Н.М.Л. Теорема Маркова
Припустимо, що всі інтенсивності потоків подій lij=const, іншими словами, усі потоки подій - найпростіші (стаціонарні пуасонівські) потоки [2;3].
Виникає питання, що буде із системою S при 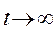 ? Чи буде функція Pi(t), i = 1, , 4, рішення системи рівнянь Колмогорова (2.21) - (2.22) прагнути до будь якої межі
? Чи буде функція Pi(t), i = 1, , 4, рішення системи рівнянь Колмогорова (2.21) - (2.22) прагнути до будь якої межі
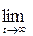 Pi(t) = Pi (2.23)
Pi(t) = Pi (2.23)
називаються граничними ймовірностями системи.
Теорема Маркова (для Н.М.Л.) Якщо число станів системи S кінцеве і з кожного стану можна перейти (за те чи інше число кроків) у кожний інший, то граничні ймовірності станів існують і не залежать від початкового стану системи.
Очевидно, що 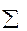 Pi = 1.
Pi = 1.
Таким чином, якщо виконується теорема Маркова для системи S(Н.М.Л.), то при 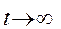 в системі S встановлюється деякий граничний стаціонарний режим: система випадковим чином змінює свої стани, але ймовірність кожного з них не залежить від часу. Ці ймовірності можна трактувати як середній відносний час перебування системи в даному стані.
в системі S встановлюється деякий граничний стаціонарний режим: система випадковим чином змінює свої стани, але ймовірність кожного з них не залежить від часу. Ці ймовірності можна трактувати як середній відносний час перебування системи в даному стані.
Наприклад, якщо у системи три стани S1; S2; S3 і їхні граничні ймовірності Р1 = 0,1; Р2 = 0,4; Р3 = 0,5, то це означає: після переходу до сталого режиму система, у середньому, 1/10 часу буде знаходитися в S1; 0,4 у S2, 0,5 у S3.
Тому що в сталому режимі усі Pi = cоnst, тобто не залежать від часу, то Pi= 0. Тоді система диференційованих рівнянь Колмогорова (21) перетвориться в систему лінійних алгебраїчних рівнянь, у яких усі ліві частини рівні нулю. Розв'язавши її з урахуванням  Pi = 1, одержимо граничні ймовірності Pi.
Pi = 1, одержимо граничні ймовірності Pi.
3. Теорія масового обслуговування (Т.М.О.)
Задача і предмет Т.М.О.
При дослідженні операцій часто приходить зіштовхуватися з аналізом систем масового обслуговування (С.М.О.).
Приклади СМО: телефонні станції, ремонтні майстерні, білетні каси, довідкові бюро, майстерні магазини і т.і.
Структура СМО:
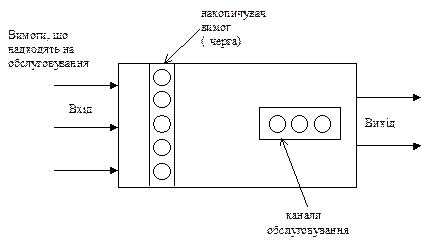 Мал. 8 Мал. 8 |
Як видно із схеми, мал.8, СМО призначена для обслуговування (виконання) якогось потоку заявок (вимог), що надходять на СМО в якісь випадкові моменти часу.
Внутрішній стан СМО характеризується наявністю якогось числа одиниць обслуговування, каналів обслуговування.
У якості каналів можуть бути: лінії зв'язку, робочі точки, прилади, ліфти і т.д.
СМО можуть бути одноканальними і багатоканальними. Обслуговування вимоги продовжується деякий (у загальному) випадковий час, після чого канал звільняється і готовий до роботи, тобто обслуговуванню наступної вимоги (заявки). Випадковий характер потоку заявок призводить до того, що в якісь проміжки часу на вході СМО утвориться зайво велике число заявок, вони або стають у чергу, або покидають СМО. У інші ж періоди СМО може працювати з недовантаженням або взагалі простоювати.
Кожна СМО в залежності від числа каналів і їхньої продуктивності, а також від характеру потоку заявок, володіє якоюсь пропускною спроможністю, що дозволяє їй більш-менш успішно справлятися з потоком заявок.
Таким чином предмет теорії М.О. - встановлення залежності між характером потоку заявок, числом каналів, їхньою продуктивністю, правилами роботи С.М.О. і успішністю (ефективністю) обслуговування.
У якості характеристик ефективності обслуговування можуть застосовуватися:
1) середня кількість заявок, яку може обслужити С.М.О. в одиницю часу;
2) середній відсоток заявок, що одержують відмову і покидають С.М.О. необслуговуваними;
3) ймовірність того, що заявка, яка надійшла, негайно буде прийнята до обслуговування;
4) середній час очікування в черзі;
5) закон розподілу часу очікування;
6) середня кількість заявок у черзі;
7) закон розподілу числа заявок у черзі;
8) середній прибуток, принесений С.М.О. в одиницю часу і т.д.
Випадкові характери потоку заявок і часу їх обслуговування призводить до того, що в С.М.О. буде відбуватися випадковий процес.
Теорія масового обслуговування займається вивченням і математичним описанням випадкових процесів, що протікають у С.М.О., із метою керування процесом.
Математичний аналіз роботи С.М.О. дуже спрощується, якщо випадковий процес, що протікає в системі є марковським, тобто щоб усі потоки подій, що переводять систему із стану у стан, були пуасонівськими (потоками без наслідків). Для С.М.О. потоки подій - це потоки заявок, потоки “обслуговування” заявок і т. і.
Властивості і характеристики пуасонівських процесів ми вже розглядали.
Нагадаємо, коли пуасонівський потік стаціонарний (найпростіший потік, l = const), інтервал часу Т між подіями в цьому потоці є випадкова величина, розподілена за показовим законом:
f(t) = le- l*t t > 0 (2.24)
де l- інтенсивність (точність) потоку подій:
У випадку, коли з якогось стану St систему виводять відразу декілька найпростіших потоків, величину Т, час перебування системи (підряд) у даному стані, є випадкова величина, розподілена за законом (2.24), де l - сумарна інтенсивність усіх потоків подій, що виводять систему з даного стану.
