История развития алгоритмов решение задачи о максимальном потоке
История развития алгоритмов решения задачи о максимальном потоке
Задача поиска максимального потока в сети в общем случае решается так же, как и известная на тот момент транспортная задача. Симплексный метод специально для этой задачи был модифицирован в 1951 году Данцигом. Алгоритм не был полиномиальным, как и любой симплексный метод. Однако специальный вид задачи позволил предположить, что для ее решения можно применить более простые и быстрые алгоритмы. Первый такой алгоритм, который не похож на симплексный метод, был разработан Фордом и Фалкерсоном в 1956 году. Время работы этого алгоритма не было полиномиальным (таблица 1), однако его идея и его математическое обоснование как раз и легли в основу качественной теории потоков. В предложенном методе использовалась идея «дополняющих путей».
В 1970 году Эдмондс, Карп и, независимо от них Диниц, улучшили алгоритм Форда и Фалкерсона, доказав теорему о том, что алгоритм выполняется за полиномиальное время, если на каждом его шаге использовать увеличивающие цепочки минимальной длины.
В следующем десятилетии алгоритмы поиска максимального потока стали быстрее благодаря новым мощным технологиям. Одну из таких технологий ввел Диниц – его идея блокирующий потоков, основанная на идее кратчайших путей, позволила не только достигнуть новых временных границ, но и дала богатую почву для новых изобретений. Однако Диниц не занимался отдельно задачей поиска блокирующего потока, показав лишь, что даже самый простой метод (1970 год) значительно улучшает оценку Эдмондса и Капа. Карзанов, разрабатывая новые методы поиска блокирующих потоков, развил идею «предпотоков», которая позволила получить самый быстрый на тот момент алгоритм поиска максимального потока для плотных сетей с оценкой O(n3). Алгоритм получил название «волновой» – название, символизирующее идею движения волны (1974 год). Еще одно изобретение в области алгоритмов – масштабирование – было создано Эдмондсом, Карпом и, независимо от них, Диницем (1972 год). Идея масштабирования пропускных способностей сети, однако, требовала, чтобы сами пропускные способности были целыми числами. Оценка времени работы алгоритмов масштабирования была псевдополиномиальной.
Идея масштабирования заключается в декомпозиции задачи поиска максимального потока не подзадачи, называемые ∆-фазами. В процессе ∆-фазы увеличение потока происходит только вдоль путей с пропускной способностью не меньшей ∆. Когда все такие пути исчерпаны, осуществляется переход на новую фазу масштабирования, путем деления ∆ на два (нацело). На последней фазе ∆=1 – выбираются любые пути, откуда следует, что в конце работы будет найден максимальный поток с точностью до 1 – это максимальная точность для сети с целыми пропускными способностями. Так как каждый раз ∆ делится на 2 нацело, требуется не более чем log2U ∆ -фаз. В 1973 году Диниц и независимо от него Габов разработали новую, другую, схему выполнения каждой отдельной фазы, не такую, которую ипользовали Эдмондс и Карп. Это позволило впервые получить оценку времени работы, в которой множитель O(nm) входит в первой степени, если опустить влияние, как правило, небольшой величины O(logU).
Таблица 1 История улучшений сложности алгоритмов поиска
максимального потока.
| Год | Авторы | Оценка сложности |
| Данциг | O(n2mU) | |
| Форд и Фалкерсон | O(nmU) | |
| Эдмонд и Карп; Диниц | O(nm2) | |
| Диниц | O(n2m) | |
| Едмондс и Карп; Диниц | O(m2logU) | |
| Диниц; Габов | O(mn logU) | |
| Карзанов | O(n3) | |
| Черкасски | O(n2√m) | |
| Шилочь | O(n(n+m)log2(n+m)) | |
| Галил и Наамад | O(nmlog2n) | |
| Слейтор и Тарьян | O(nmlogn) | |
| Голдберг и Тарьян | O(nmlog(n2/m)) | |
| Ахьюджи и Орлин | O(nm+n2logU) | |
| Ахьюджи и др. | O(nmlog(n/m*√logU)) | |
| Черкасски и Хагерап | E(nm+n2logU)3 | |
| Чериян и др | O(n3/logn) | |
| Алон | O(nm+n8/3logn | |
| Кинг и др. | O(nm+n2+e) | |
| Филипс и Вестбрук | O(nm(logm/nn+log2+en)) | |
| Кинг | O(nmlogm/(nlogn)n) | |
| Голдберг и Рао | O(min(n2/3,m1/2)mlog(n2/m)logU) |
История улучшений сложности алгоритмов поиска максимального потока. Оценки, содержащие U (зависят от максимальной пропускной способности), - применяются к сетям с целыми пропускными способностями. n - число вершин в сети, m - число ребер.
В 1970 году Диниц разработал идею блокирующих потоков, которая, как уже было сказано, привнесла множество открытий в области разработки алгоритмов поиска максимального потока. Многие алгоритмы отличаются только способом поиска блокирующих потоков, которых было придумано огромное множество. Например, Йоши Шилочь использовал сбалансированные деревья, чтобы научиться находить блокирующий поток за время O(I log2I), где I=n+m.
В 1974 году идея предпотоков Карзанова также продвинула алгоритмы к новой оценке – O(n3) , которая до конца XX века являлась лучшей для произвольных плотных сетей. И не только это было открытием – идея предпотоков была использована Голдбергом для создания совершенно новой идеи поиска потоков – методов проталкивания самый простой из которых выполнялся за время O(n2m), а его несложные модификации 4 позволили получить оценку O(n3, чем Голдберг и повторил результат Карзанова. На сегодняшний день самые быстрые алгоритмы используют именно идею проталкивания. В 1986 году Голдберг и Тарьян разработали новый алгоритм на основе проталкивания, позволивший достигнуть оценки O(nm log(n2/m))Алгоритм использует структуру данный, называемую деревом Слейтора-Тарьяна. В 1983 году Слейтор и Тарьян использовали эту структуру для усовершенствования алгорима Диница, чем получили оценку O(nm log n).
В 1987 году Ахъюджи и Орлин объединили идеи Голдберга и идею масштабирования, получив оценку O(nm+n2log U). В отличие от Габова и Диница, они масштабировали не пропускную способность ребер, а избыток потока в вершине в алгоритме «проталкивания предпотока» Голдберга. Несложная модификация их метода (без использования таких структур, как сбалансированные или динамические деревья) выполнялась за время O(nmlog(n/m*√ log U)) .
Для единичный сетей Карзанов и независимо от него Тарьян и Эвен показали, что алгоритм Диница, использующий блокирующие потоки требует всего лишь O(min(n2/3, m1/2)m) для графов без мультидуг и O(m3/2) для мультиграфов. Этот эффект достигается как раз за счет идеи приближения максимального потока последовательностью блокирующих потоков, которая для единичных сетей сходится быстрее. Было обнаружено, что поиск максимального потока для таких сетей может быть отдельной задачей, которая обладает своими особенными свойствами. Кроме единичных сетей так же рассматривались простые сети – для них алгоритм Диница выполняется за время O(m√n), что позволило достигнуть новой оценки для задачи о максимальном паросочетании.
Задачи поиска максимального потока поделились на два основных класса – поиск максимального потока в сети с целыми пропускными способностями в сети с единичными пропускными способностями. Долгое время алгоритмы поиска максимального потока в сети с целыми пропускными способностями «держались» на оценке, близкой к O(nm), однако были «хуже» нее, в то время как алгоритмы для единичных сетей эту оценку сильно превзошли. Но в 1997 году Голдберг и Рао использовали идею нелинейной функции расстояния, идеи Диница и деревья Слейтора-Тарьяна, чтобы получить алгоритм с оценкой
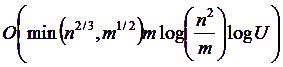 |
который и на сегодняшний день остается самым быстрым и который резко сократил расстояние между единичными и целочисленными сетями, показав, что оценка O(nm) даже очень скромная для задачи поиска максимального потока.
Идея нелинейной функции расстояния была придумана еще Эдмондсом и Карпом, однако она не давала такого существенного улучшения оценки. Эдмондс и Карп использовали нелинейную функцию расстояния в градиентной модификации метода Форда-Фалкерсона. На каждом шаге выполнялся поиск самого пропускного пути, для чего требовалось модифицировать алгоритм Дейкстры для поиска пути минимальной длины. Новый алгоритм давал незначительное улучшение оценки и не получил широкого распространения, однако идея использования нелинейной функции расстояния, как мы видим была реабилитирована Голбергом и Рао.
В процессе работы над совершенствованием алгоритмов было изобретено несколько структур данных. Например, как уже упоминалось, в 1978 году Шилочь использовал сбалансированные деревья для своей структуры данных, поддерживающей быструю работу с дополняющими путями, что позволило усовершенствовать алгоритм поиска блокирующего потока и получить новую оценку. Слейтор и Тарьян разработали специальную структуру динамических деревьев, с помощью которой в 1983 году пыла получена новая для того времени оценка сложности поиска блокирующего потока – O(m log n). Деревья Слейтора-Тарьяна получили широкое применение для решения многих других задач, таких, как задача о поиске наименьшего общего предка, поиске минимального покрывающего дерева и т. д. Кроме этого, современные быстрые алгоритмы используют именно эту структуру данных.
