Решение показательных неравенств
| Основания степеней одинаковые больше 1, при переходе к неравенству с показателями, знак неравенства сохраняется. | 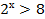 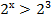 х х 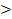 3 3 | Основание степеней одинаковые больше 0, но меньше 1, при переходе к неравенству с показателями необходимо изменить знак неравенства на противоположный. | 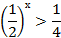 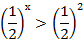 х х 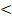 2 2 |
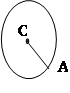
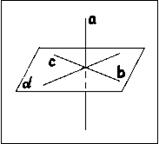 Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости. Признак перпендикулярности прямой и плоскости. Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.
Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости. Признак перпендикулярности прямой и плоскости. Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости. 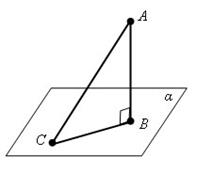 Отрезок АВ – перпендикуляр, проведенный из точки А к плоскости a. Точка В – основание перпендикуляра. Отрезок АС – наклонная, проведенная из точки А к плоскости a. Отрезок ВС называется проекцией наклонной на плоскость a. Теорема о трех перпендикулярах. Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна к наклонной.
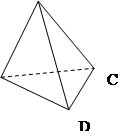
Отрезок АВ – перпендикуляр, проведенный из точки А к плоскости a. Точка В – основание перпендикуляра. Отрезок АС – наклонная, проведенная из точки А к плоскости a. Отрезок ВС называется проекцией наклонной на плоскость a. Теорема о трех перпендикулярах. Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна к наклонной. | Тетраэдр Точки А,В,С,D – 4 вершины тетраэдра. Отрезки АВ, АС, А D, ВС, В D,С D - 6 ребер тетраэдра. Треугольники АСВ, ВС D,АС D, АВ D – 4 грани тетраэдра |
| |||||||||||||
| Параллелепипед. Параллелограммы , из которых составлен параллелепипед –грани (их 6), их стороны – ребра ( их 12), а вершины параллелограммов – вершины параллелепипеда. | 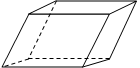 |
7.Свойства параллелепипеда:
А) Противоположные грани параллелепипеда параллельны и равны.
Б) Диагонали параллелепипеда, пересекаются в одной точке и делятся этой точкой пополам.
8.Сечением называется многоугольник, сторонами которого являются отрезки различных граней многогранника.
| 9. Сечением тетраэдра может быть треугольник, четырехугольник. | Сечением параллелепипеда может быть треугольник, четырехугольник, пятиугольник, шестиугольник. |
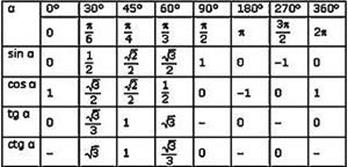 sinx=а: x=(-1)narcsinа+pn, n
sinx=а: x=(-1)narcsinа+pn, n Z; 2. cosx=а: x=+arccosа+2pn, n
Z; 2. cosx=а: x=+arccosа+2pn, n Z; tgx=а: x=arctgа+pn, n
Z; tgx=а: x=arctgа+pn, n  Z
Z 
| 2. Призма | 3. Виды призм |
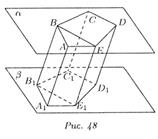 Многоугольники ABCDE и А1В1С1D1E1 – основания призмы. Параллелограммы АВВ1А1 и т.д. – боковые грани. Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы. Многоугольники ABCDE и А1В1С1D1E1 – основания призмы. Параллелограммы АВВ1А1 и т.д. – боковые грани. Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы. 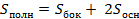 Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы. Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы. | Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой, в противном случае - наклонной. 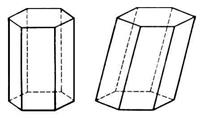 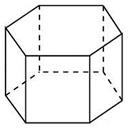 Прямая призма Наклонная призма Прямая призма называется правильной, если ее основания – правильные многоугольники. Прямая призма Наклонная призма Прямая призма называется правильной, если ее основания – правильные многоугольники. |
| 4. Пирамида | 5. Правильная пирамида |
-многогранник, составленный из n-угольника и n треугольников. 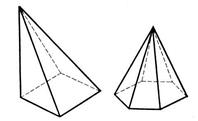 Площадью полной поверхности пирамиды называется сумма площадей всех ее граней, а площадью боковой поверхности – сумма площадей ее боковых граней. Площадью полной поверхности пирамиды называется сумма площадей всех ее граней, а площадью боковой поверхности – сумма площадей ее боковых граней. 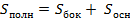 | 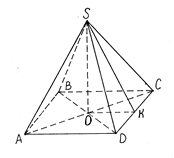 –пирамида, основание которой правильный многоугольник, а отрезок, соединяющий вершину пирамиды с ценром основания, является ее высотой (SO). Апофема -высота боковой грани правильной пирамиды, проведенная из ее вершины. (SK) Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему. –пирамида, основание которой правильный многоугольник, а отрезок, соединяющий вершину пирамиды с ценром основания, является ее высотой (SO). Апофема -высота боковой грани правильной пирамиды, проведенная из ее вершины. (SK) Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему. |
| Производная суммы (f + g)` = f` + g` | Производная произведения (f g) `= f ` g + f g` |
Производная частного(  )` = )` = 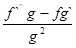 | Производная сложной функции (f(g))` = f`(g) g` |
Таблица производных ( 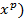 ` = ` = 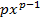 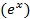 ` = ` = 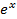 (lnx)` = (lnx)` =  (sinx) `= cosx (cosx)` = - sinx (tgx)`= (sinx) `= cosx (cosx)` = - sinx (tgx)`= 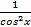 (ctgx)` = (ctgx)` = 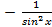 | Геометрический смысл производной F ` ( 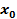 ) = k = tg ) = k = tg 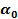 , где k – угловой коэффициент касательной, проведенной к графику функции в точке с абсциссой , где k – угловой коэффициент касательной, проведенной к графику функции в точке с абсциссой 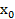 ; α – угол между касательной и положительным направлением оси абсцисс ; α – угол между касательной и положительным направлением оси абсцисс |
| Цилиндр | Конус | |||
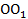 - ось цилиндра - ось цилиндра      l – образующая r – радиус основания l – образующая r – радиус основания  h – высота l h h – высота l h
r
|    PO- ось цилиндра P l – образующая r – радиус основания PO- ось цилиндра P l – образующая r – радиус основания   h – высота l h r h – высота l h r 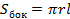 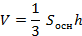 | |||
 Сфера и шар Сфера и шар
|
Формулы планиметрии, полезные при решении стереометрических задач
Прямоугольный треугольник 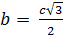 ;
; 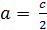
Равносторонний треугольник 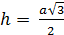 ;
; 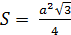
Квадрат 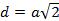
Свойство точки пересечения медиан треугольника. Точка пересечения медиан треугольника делит каждую его медиану в отношении 2:1, считая от вершины.
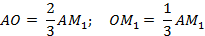

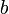 по основанию
по основанию 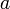 определяется как показатель степени, в которую надо возвести число a, чтобы получить число b, где
определяется как показатель степени, в которую надо возвести число a, чтобы получить число b, где 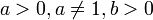 2. Основное логарифмическое тождество
2. Основное логарифмическое тождество 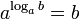 , где
, где 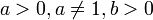 3. Свойства логарифмов а)
3. Свойства логарифмов а) 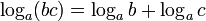 б)
б) 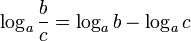 в)
в) 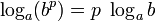 г)
г) 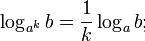 д)
д) 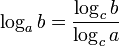 4. Логарифмическая функция
4. Логарифмическая функция 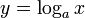 . Она определена при
. Она определена при 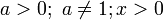 5. График логарифмической функции
5. График логарифмической функции 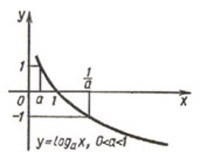
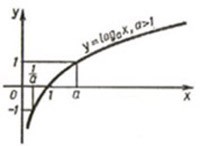 6. Логарифмические уравнения При решении логарифмических уравнений необходимо найти область определения уравнения или в конце сделать проверку.
6. Логарифмические уравнения При решении логарифмических уравнений необходимо найти область определения уравнения или в конце сделать проверку. 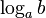 имеет смысл при
имеет смысл при 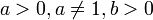 7. Логарифмические неравенства
7. Логарифмические неравенства | log a f(x) > log a g(x) при a > 1 знак неравенства не меняется f(x) > g(x) | log a f(x) > log a g(x) при 0 < a < 1 знак неравенства меняется f(x) < g(x) |
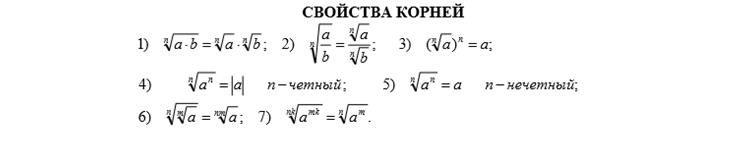


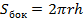
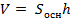

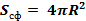
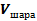 =
= 