Прямая линия на плоскости
Векторная алгебра.
Условие коллинеарности(параллельности) векторов 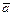 и
и 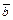 :
: 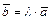 или
или 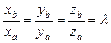 , где
, где 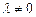 .
.
Орт вектора 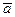 - вектор
- вектор 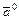 , имеющий единичную длину и направление вектора
, имеющий единичную длину и направление вектора 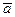 :
: 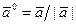 .
.
Проекция вектора 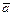 на вектор
на вектор 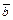 - число
- число 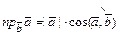 .
.
Действия над векторами в координатной форме:
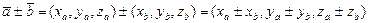 ;
; 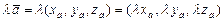 .
.
Длина 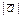 вектора
вектора 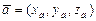 :
: 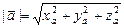 .
.
Направляющие косинусывектора 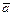 - числа:
- числа:
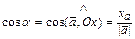 ,
, 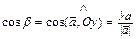 ,
, 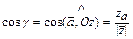 , при этом
, при этом 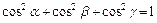 .
.
Координаты вектора 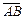 , заданного точками
, заданного точками 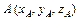 и
и 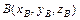 :
: 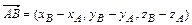 .
.
Расстояние 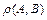 между точками
между точками 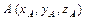 и
и 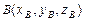 :
:
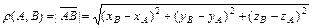 .
.
Координаты точки 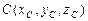 , делящей отрезок
, делящей отрезок 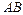 пополам:
пополам: 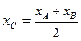 ,
, 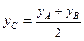 ,
, 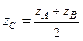 .
.
Скалярное произведение векторов.
Скалярное произведениененулевых векторов 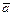 и
и 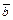 - число:
- число: 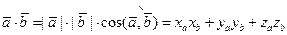 .
.
Скалярное произведение обладает свойствами:
1) 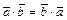 ; 2)
; 2) 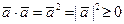 ; 3)
; 3) 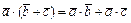 ; 4)
; 4) 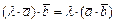 ,где
,где 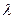 - число;
- число;
Для векторов канонического базиса 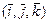 :
: 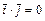 ,
, 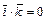 ,
, 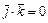 ,
, 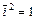 ,
, 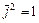 ,
, 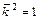 .
.
Некоторые приложения скалярного произведения:
1) Вычисление угла между векторами 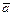 и
и 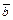 :
: 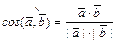 .
.
2) Установление перпендикулярности векторов 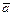 и
и 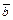 :
: 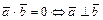 .
.
3) Нахождение проекции вектора 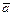 на вектор
на вектор 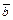 :
: 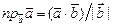 .
.
Векторное произведение векторов.
Векторное произведение векторов 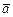 и
и 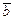 - вектор
- вектор 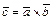 , определяемый условиями:
, определяемый условиями:
1) 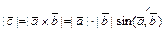 ; 2)
; 2) 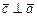 и
и 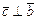 ; 3)
; 3) 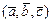 - правая тройка векторов.
- правая тройка векторов.
Векторное произведение обладает свойствами:
1) 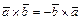 ; 2)
; 2) 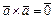 3)
3) 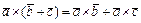 ; 4)
; 4) 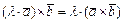 ,где
,где 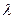 - число;
- число;
Для векторов канонического базиса 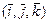 :
: 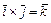 ,
, 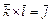 ,
, 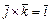 ,
, 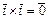 ,
, 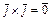 ,
, 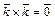 .
.
Для векторов 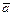 и
и 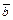 , заданных координатами
, заданных координатами 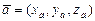 ,
, 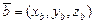 :
: 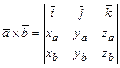
Некоторые приложениявекторного произведения:
1) Вычисление площадей треугольника и параллелограмма: 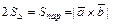 .
.
2) Установление параллельности векторов 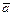 и
и 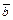 :
: 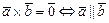 .
.
Смешанное произведение векторов.
Смешанное произведение упорядоченной тройки векторов 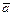 ,
, 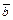 и
и 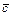 - число
- число 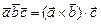
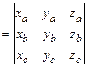 . Смешанное произведение обладает свойствами:
. Смешанное произведение обладает свойствами:
1) 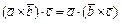 ; 2)
; 2) 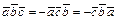 ; 3)
; 3) 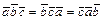 ; 4)
; 4) 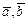 и
и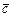 -компланарны
-компланарны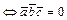 ;
;
Некоторые приложениясмешанного произведения:
1) Вычисление объёмов тетраэдра и параллелепипеда: 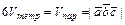 .
.
2) Установление компланарности векторов 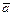 ,
, 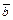 и
и 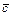 :
: 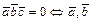 и
и 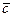 - компланарны.
- компланарны.
3)Установление базиса в пространстве: 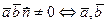 и
и 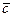 - базис.
- базис.
3)Установление принадлежности четырёх точек 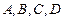 одной плоскости:
одной плоскости: 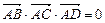
Аналитическая геометрия
Прямая линия на плоскости.
1) 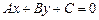 - общее уравнение прямой, где
- общее уравнение прямой, где 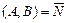 - нормальный вектор прямой;
- нормальный вектор прямой;
2) 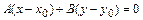 - уравнение прямой, проходящей через точку
- уравнение прямой, проходящей через точку 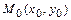
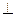 вектору
вектору 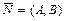 ;
;
3) 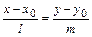 - уравнение прямой, проходящей через точку
- уравнение прямой, проходящей через точку 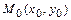
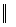 вектору
вектору 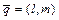 (каноническое уравнение);
(каноническое уравнение);
4) 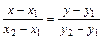 - уравнение прямой, проходящей через две данные точки
- уравнение прямой, проходящей через две данные точки 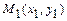 ,
, 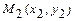 ;
;
5) 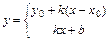 -уравнения прямой с угловым коэффициентом
-уравнения прямой с угловым коэффициентом 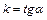 , где
, где 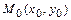 - точка через которую прямая проходит;
- точка через которую прямая проходит; 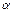 (
( 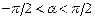 ) – угол прямой осью
) – угол прямой осью 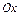 ;
; 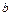 - длина отрезка (со знаком
- длина отрезка (со знаком 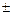 ), отсекаемого прямой на оси
), отсекаемого прямой на оси 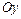 ( «
( « 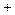 », если на положительной части оси и «
», если на положительной части оси и « 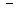 », если на отрицательной).
», если на отрицательной).
6) 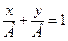 -уравнение прямой в отрезках, где
-уравнение прямой в отрезках, где 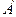 и
и 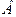 - длины отрезков (со знаком
- длины отрезков (со знаком 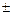 ), отсекаемых прямой на координатных осях
), отсекаемых прямой на координатных осях 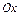 и
и 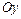 ( «
( «  », если на положительной части оси и «
», если на положительной части оси и «  », если на отрицательной).
», если на отрицательной).
Расстояние от точки 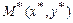 до прямой
до прямой 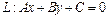 :
: 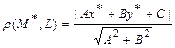 .
.
Угол 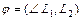 , (
, ( 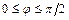 ) между прямыми
) между прямыми 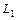 и
и 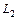 :
: 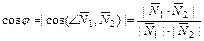 ;
; 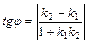 .
.
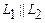 , если
, если 
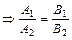 или
или 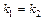 .
.
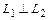 ,если
,если 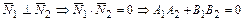 или
или 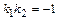
Координаты точки пересечения прямых 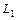 и
и 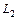 :
: 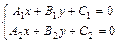 или
или 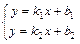 .
.
Плоскость.
1) 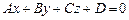 - общее уравнение плоскости, где
- общее уравнение плоскости, где 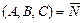 - нормальный вектор плоскости;
- нормальный вектор плоскости;
2) 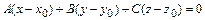 - уравнение плоскости, проходящей через точку
- уравнение плоскости, проходящей через точку 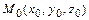
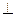 вектору
вектору 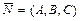 ;
;
3) 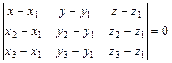 - уравнение плоскости, проходящей через три точки
- уравнение плоскости, проходящей через три точки 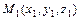 ,
, 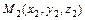 и
и 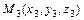 ;
;
4) 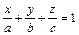 -уравнение плоскости в отрезках, где
-уравнение плоскости в отрезках, где 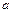 ,
, 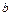 и
и 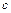 - дины отрезков (со знаком
- дины отрезков (со знаком 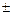 ), отсекаемых плоскостью на осях
), отсекаемых плоскостью на осях 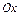 ,
, 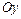 и
и 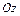 ( «
( « 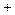 », если на положительной части оси и «
», если на положительной части оси и « 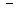 », если на отрицательной).
», если на отрицательной).
Расстояние от точки 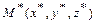 до плоскости
до плоскости 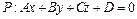 :
: 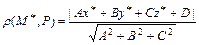 .
.
Угол 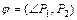 , (
, ( 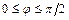 ) между плоскостями
) между плоскостями 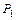 и
и 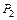 :
: 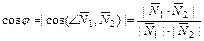 .
.
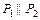 , если
, если 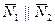
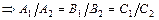
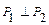 , если
, если 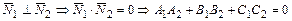 .
.
