Поляризация световых волн

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

Высшего профессионального образования

НАЦИОНАЛЬНЫЙ МИНЕРАЛЬНО-СЫРЬЕВОЙ УНИВЕРСИТЕТ «ГОРНЫЙ»

Кафедра общей и технической физики

Общая физика

ВОЛНОВАЯ ОПТИКА

Поляризация световых волн.

Искусственная оптическая анизотропия

Лабораторный практикум

САНКТ-ПЕТЕРБУРГ

УДК 535.41/42 + 535.5 (075.80)

ББК 22.34

Общая физика. ВОЛНОВАЯ ОПТИКА. Поляризация световых волн. Искусственная оптическая анизотропия: Лабораторный практикум / А.С.Мустафаев, С.В. Егоров. Национальный минерально-сырьевой университет «Горный». СПб, 2012. 38 с.

ISBN 5-94211-162-6

В лабораторном практикуме представлены работы по всем основным оптическим явлениям: дисперсии, поляризации, поглощению света, искусственной оптической анизотропии, вызываемой электромагнитными полями, и вращению плоскости поляризации.

Практикум предоставляет возможность студентам познакомиться с явлениями, лежащими в основе современных оптических технологий. Основная задача - овладеть техникой и методикой проведения экспериментальных исследований, а также приемами обработки результатов исследований и оформления заключительного отчета.

В зачетных работах практикума, выполняемых по индивидуальной программе, студент должен продемонстрировать умение в устной и письменной форме, логически верно, и аргументировано защищать результаты своих исследований.

Лабораторный практикум предназначен для студентов, бакалавров и магистров всех специальностей и форм обучения Санкт-Петербургского государственного горного университета.

В постановке работ № 3, 4 и оформлении лабораторного практикума принимали участие ассистенты профессора, студенты группы ИЗ-09-3: Апалонов Иван, Горюнова Лолита.

Научный редактор проф. А.С. Мустафаев

Ó Национальный минерально-сырьевой университет «Горный»,2012 г.

ПОЛЯРИЗАЦИЯ СВЕТОВЫХ ВОЛН

Работа 1. ИССЛЕДОВАНИЕ ПОЛЯРИЗОВАННОГО СВЕТА

Теоретические сведения

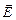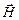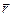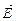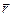Видимый свет, как известно, представляет собой электромагнитные волны с длинами волн от 4×10^–7 м (фиолетовый) до 7×10^–7 м (красный). В электромагнитной волне векторы напряженности электрического поля и магнитного поля взаимно перпендикулярны и одновременно перпендикулярны направлению распространения волны (рис.1). Плоскость, проведенную через направления и , называют плоскостью колебаний электрического вектора.

Для полной характеристики волны задают ее длину l, модули векторов 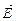и 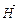и ориентацию в пространстве плоскости колебаний электрического вектора. Если для некоторого пучка света плоскость колебаний электрического вектора не изменяет положение в пространстве, то такой свет называют линейно-поляризованным.

Естественный или неполяризованный свет можно рассматривать как наложение многих электромагнитных волн, распространяющихся в одном и том же направлении, но со всевозможными ориентациями плоскостей колебаний. Таким образом, для неполяризованного света нельзя указать даже плоскость преимущественного расположения вектора напряженности электрического поля 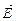. Все ориентации этого вектора равновероятны. Если же имеется какое-либо преимущественное направление ориентации вектора 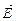, то световой пучок называют частично поляризованным.

Если в световом пучке вектор 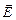имеет составляющие как по оси х, так и по оси у, причем 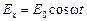и 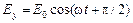, где w – частота световой волны, то в каждый момент времени t эти составляющие складываются. Результирующий вектор, оставаясь постоянным по величине, вращается с частотой w, а его конец описывает окружность. В этом случае говорят, что свет имеет круговую поляризацию.

Если составляющие вектора 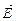по осям х и у колеблются с одинаковыми частотами, но имеют либо разные амплитуды, либо разность фаз колебаний отличается от 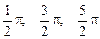и т.д., то конец электрического вектора будет описывать эллипс и в этом случае говорят об эллиптической поляризации светового пучка. Таким образом, имеется пять типов поляризованного света:

· естественный или неполяризованный свет;

· частично поляризованный свет;

· линейно или плоско поляризованный свет;

· свет, поляризованный по кругу;

· эллиптически поляризованный свет.

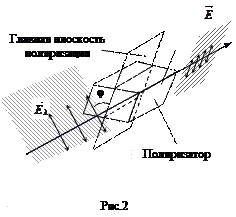Пусть на поляризатор падает плоскополяризованное излучение интенсивностью I₀ (рис.2). Разложим вектор 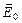на две составляющие, лежащие в главной плоскости поляризатора: Е_|| = Е₀cosj, и перпендикулярную составляющую E_^ = E₀sinj, где j – угол между плоскостью колебаний электрического вектора, падающего на поляризатор излучения, и главной плоскостью поляризатора. Поскольку поляризатор пропускает излучение только с составляющей вектора 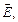лежащей в главной плоскости, то выходящее излучение имеет интенсивность

I ~ < E_||² > = < E₀² cos²j >,

здесь угловые скобки обозначают, усреднение по времени. Учитывая, что интенсивность падающего излучения I₀~ <E₀²>, получим

I = I₀cos²j. (1)

Последнее соотношение называют законом Малюса.

Если направить на поляризатор естественное (неполяризованное) излучение, в котором все ориентации вектора напряженности равновероятны (т.е. возможны любые значения j), то проводя усреднение по углу j в соотношении (1) получим I = 0,5 I_ест. Таким образом, при прохождении через поляризатор естественное излучение становится линейно-поляризованным, но убывает по интенсивности вдвое.

Для количественной оценки степени поляризацииизлучения применяется соотношение

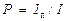. (2)

Частично поляризованное излучение понимается как смесь линейно поляризованного и неполяризованного излучений. Тогда I – полная интенсивность, I_п – интенсивность линейно-поляризованного компонента. Очевидно, 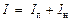, где I_н – интенсивность неполяризованного компонента. Поскольку 0 < I_н< I, то степень поляризации может меняться в пределах 0 < Р< 1.

Если направить частично поляризованное излучение на поляризатор и вращать устройство, меняя угол между главной плоскостью поляризатора и преимущественным направлением вектора 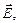то интенсивность прошедшего излучения будет меняться от максимального значения I_max до минимального I_min. В первом положении поляризованный компонент проходит полностью, а неполяризованный уменьшается по интенсивности вдвое:

I_max = I_п + I_н / 2. (3)

Во втором положении, которое отличается по углу от первого на 90°, поляризованный компонент, согласно закону Малюса, полностью задерживается, а неполяризованный по-прежнему умень­шается вдвое:

I_min = I_н/ 2. (4)

Складывая и вычитая уравнения (3) и (4), имеем 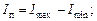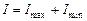. Подставляя последние соотношения в (2) получим формулу для расчета степени поляризации при обработке экспериментальных данных:

Р = (I_max – I_min) / (I_max + I_min). (5)

Способ получения эллиптически поляризованного излучения. Допустим, что из двоякопреломляющего кристалла вырезана пластинка таким образом, что оптическая ось лежит в плоскости среза. Допустим далее, что излучение падает на пластинку перпендикулярно плоскости среза. В этом случае колебания электрического вектора, как в обыкновенной волне ( 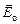), так и в необыкновенной ( 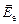) совершаются согласованно (когерентно). И в дальнейшем будем индексом о - обозначать обыкновенную волну; индексом е – необыкновенную.

Направления электрических векторов обыкновенного и необыкновенного лучей взаимноперпендикулярны. И эти лучи распространяются в одном направлении, но с разными скоростями. В связи с этим, при прохождении через пластинку между ними возникает разность хода:

DL = (n_o – n_e)d, (6)

где d – толщина кристаллической пластинки; n_o и n_e показатели преломления обыкновенного и необыкновенного лучей.

Как уже отмечалось, при наличии разности хода волны могут интерферировать только в том случае, если они когерентны. Если падающее на кристалл излучение не поляризовано, о - и е-волны испускаются разными группами атомов (не согласованно), поэтому волны не когерентны. Если же на кристалл падает линейно-поляризованный свет, то волна разделяется между о- и е-волнами в пропорции, которая зависит от ориентации плоскости колебаний. Поэтому возникающие о- и е-компоненты когерентны и способны интерферировать.

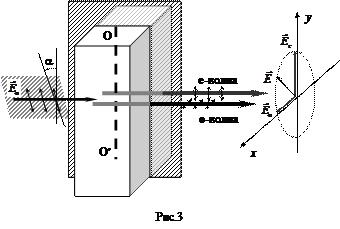
Из теории сложения колебаний известно, что при сложении взаимно перпендикулярных колебаний одинаковой частоты конец результирующего вектора 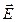движется по эллипсу (рис.3):

x²/E_о² – (2xy/E_оE_е) cos (dj) + y²/ E_е² = sin²(dj),

где dj – сдвиг фаз колебаний на выходе из пластинки кристалла; x и y – координаты конца результирующего вектора 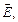x º E_x, y º E_y.

Нас интересует случай, когда эллипс ориентирован своими полуосями по осям Оx и Оy (Оу лежит в главной плоскости кристалла), при этом E_oи E_eявляются полуосями эллипса. Это наблюдается, если выполнено условие для разности фаз: 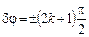, k = 0, 1, 2, … Уравнение эллипса преобразуется при этом к виду

E_x²/E_о² + E_y²/E_e² = 1.

Разность фаз колебаний связана с разностью хода лучей: dj = 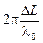. Используя (6), получим

d(n_o – n_e) = ±(λ₀/4 + kλ). (7)

Здесь знак плюс соответствует отрицательным кристаллам (n_o> n_e), знак минус – положительным кристаллам (n_o < n_e). Таким образом, если толщина пластины, вырезанной вдоль оптической оси, удовлетворяет условию (7), результатом будет эллиптическая поляризация выходящего излучения. Такая пластина носит название четвертьволновой или пластины λ/4.

Способ полученияциркулярной (круговой) поляризации излучения. Эллипс превращается в окружность при равенстве полуосей эллипса, т.е. E_o = E_e º E. Этого достигают, ориентируя четвертьволновую пластину оптической осью под углом a = 45° к плоскости колебаний падающего излучения. При этом компоненты результирующего вектора 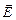удовлетворяют уравнению окружности: E_x² + E_y² = E². Заметим, что при a = 0° и a = 90° из четвертьволновой пластины выходит плоскополяризованное излучение (электрический вектор 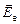в первом случаеи 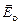во втором).

Описание экспериментальной установки

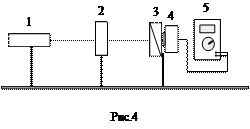Излучение полупроводникового лазера 1 (рис.4) близко к линейно-поляризованному. В первом случае (без четвертьволновой пластинки 2) оно направляется на анализатор 3 и затем попадает на фотодетектор 4. Фототок, пропорциональный интенсивности света, прошедшего через анализатор, измеряется микроамперметром 5, включенным в режиме измерения тока.

Полупроводниковый лазер находится в цилиндрическом кожухе, укрепленном на стойке.

Анализатор 3 укреплен в поворотном элементе со шкалой отсчета угла в градусах и зубчатым колесом, облегчающим вращение. Четвертьволновая пластина 2 смонтирована в круглой вращающейся оправе, на которой по ободу нанесена шкала для измерения угла поворота.

Переключатель режимов работы микроамперметра (шунт) до начала и после окончания измерений должен находиться в положении «¥». В этом случае прибор отключен и можно проверить нулевое положение светового указателя микроамперметра. Затем шунт переключают в положение, при котором регистрируется сигнал (положение «1 мкА» или «5 мкА») и проводят измерения.

Порядок выполнения работы