Биологический прототип
Развитие искусственных нейронных сетей вдохновляется биологией. То есть рассматривая сетевые конфигурации и алгоритмы, исследователи мыслят их в терминах организации мозговой деятельности. Но на этом аналогия может и закончиться. Наши знания о работе мозга столь ограничены, что мало бы нашлось руководящих ориентиров для тех, кто стал бы ему подражать. Поэтому разработчикам сетей приходится выходить за пределы современных биологических знаний в поисках структур, способных выполнять полезные функции. Во многих случаях это приводит к необходимости отказа от биологического правдоподобия, мозг становится просто метафорой, и создаются сети, невозможные в живой материи или требующие неправдоподобно больших допущений об анатомии и функционировании мозга.
Несмотря на то что связь с биологией слаба и зачастую несущественна, искусственные нейронные сети продолжают сравниваться с мозгом. Их функционирование часто напоминает человеческое познание, поэтому трудно избежать этой аналогии. К сожалению, такие сравнения неплодотворны и создают неоправданные ожидания, неизбежно ведущие к разочарованию. Исследовательский энтузиазм, основанный на ложных надеждах, может испариться, столкнувшись с суровой действительностью, как это уже однажды было в шестидесятые годы, и многообещающая область снова придет в упадок, если не будет соблюдаться необходимая сдержанность.
Несмотря на сделанные предупреждения, полезно все же знать кое-что о нервной системе млекопитающих, так как она успешно решает задачи, к выполнению которых лишь стремятся искусственные системы. Последующее обсуждение весьма кратко. Приложение А содержит более обширное (но ни в коем случае не полное) рассмотрение нервной системы млекопитающих для тех, кто хочет узнать больше об этом восхитительном предмете.
Нервная система человека, построенная из элементов, называемых нейронами, имеет ошеломляющую сложность. Около 1011 нейронов участвуют в примерно 1015 передающих связях, имеющих длину метр и более. Каждый нейрон обладает многими качествами, общими с другими элементами тела, но его уникальной способностью является прием, обработка и передача электрохимических сигналов по нервным путям, которые образуют коммуникационную систему мозга.
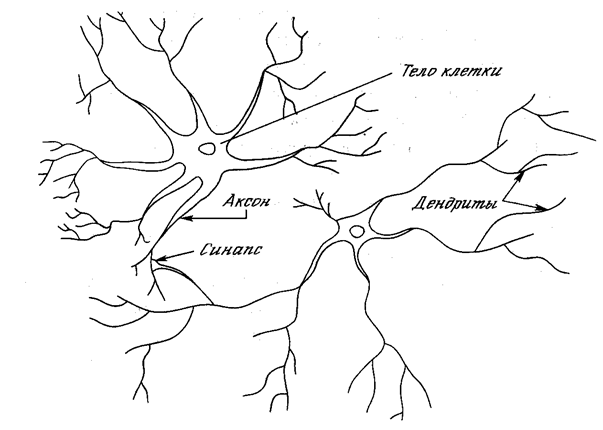
Рис. 1.1. Биологический нейрон
На рис. 1.1 показана структура пары типичных биологических нейронов. Дендриты идут от тела нервной клетки к другим нейронам, где они принимают сигналы в точках соединения, называемых синапсами. Принятые синапсом входные сигналы подводятся к телу нейрона. Здесь они суммируются, причем одни входы стремятся возбудить нейрон, другие – воспрепятствовать его возбуждению. Когда суммарное возбуждение в теле нейрона превышает некоторый порог, нейрон возбуждается, посылая по аксону сигнал другим нейронам. У этой основной функциональной схемы много усложнений и исключений, тем не менее большинство искусственных нейронных сетей моделируют лишь эти простые свойства.
ИСКУССТВЕННЫЙ НЕЙРОН
Искусственный нейрон имитирует в первом приближении свойства биологического нейрона. На вход искусственного нейрона поступает некоторое множество сигналов, каждый из которых является выходом другого нейрона. Каждый вход умножается на соответствующий вес, аналогичный синаптической силе, и все произведения суммируются, определяя уровень активации нейрона. На рис. 1.2 представлена модель, реализующая эту идею. Хотя сетевые парадигмы весьма разнообразны, в основе почти всех их лежит эта конфигурация. Здесь множество входных сигналов, обозначенных x1, x2,…, xn, поступает на искусственный нейрон. Эти входные сигналы, в совокупности обозначаемые вектором X, соответствуют сигналам, приходящим в синапсы биологического нейрона. Каждый сигнал умножается на соответствующий вес w1, w2,…, wn, и поступает на суммирующий блок, обозначенный Σ. Каждый вес соответствует «силе» одной биологической синаптической связи. (Множество весов в совокупности обозначается вектором W.) Суммирующий блок, соответствующий телу биологического элемента, складывает взвешенные входы алгебраически, создавая выход, который мы будем называть NET. В векторных обозначениях это может быть компактно записано следующим образом:
NET = XW.
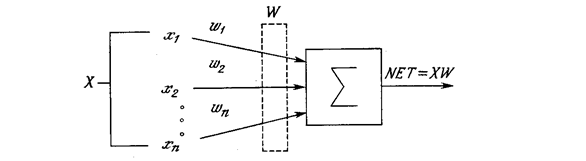
Рис. 1.2. Искусственный нейрон
Активационные функции
Сигнал NET далее, как правило, преобразуется активационной функцией F и дает выходной нейронный сигнал OUT. Активационная функция может быть обычной линейной функцией
OUT = K(NET),
где К – постоянная, пороговой функции
OUT = 1, если NET > T,
OUT = 0 в остальных случаях,
где Т – некоторая постоянная пороговая величина, или же функцией, более точно моделирующей нелинейную передаточную характеристику биологического нейрона и представляющей нейронной сети большие возможности.
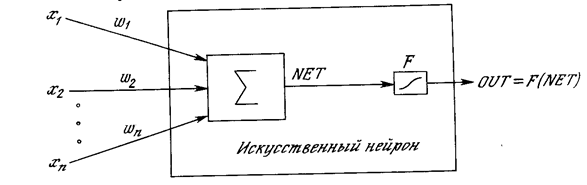
Рис. 1.3. Искусственный нейрон с активационной функцией
На рис. 1.3 блок, обозначенный F, принимает сигнал NET и выдает сигнал OUT. Если блок F сужает диапазон изменения величины NET так, что при любых значениях NET значения OUT принадлежат некоторому конечному интервалу, то F называется «сжимающей» функцией. В качестве «сжимающей» функции часто используется логистическая или «сигмоидальная» (S-образная) функция, показанная на рис. 1.4а. Эта функция математически выражается как F(x) = 1/(1 + е-x). Таким образом,
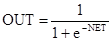 .
.
По аналогии с электронными системами активационную функцию можно считать нелинейной усилительной характеристикой искусственного нейрона. Коэффициент усиления вычисляется как отношение приращения величины OUT к вызвавшему его небольшому приращению величины NET. Он выражается наклоном кривой при определенном уровне возбуждения и изменяется от малых значений при больших отрицательных возбуждениях (кривая почти горизонтальна) до максимального значения при нулевом возбуждении и снова уменьшается, когда возбуждение становится большим положительным. Гроссберг (1973) обнаружил, что подобная нелинейная характеристика решает поставленную им дилемму шумового насыщения. Каким образом одна и та же сеть может обрабатывать как слабые, так и сильные сигналы? Слабые сигналы нуждаются в большом сетевом усилении, чтобы дать пригодный к использованию выходной сигнал. Однако усилительные каскады с большими коэффициентами усиления могут привести к насыщению выхода шумами усилителей (случайными флуктуациями), которые присутствуют в любой физически реализованной сети. Сильные входные сигналы в свою очередь также будут приводить к насыщению усилительных каскадов, исключая возможность полезного использования выхода. Центральная область логистической функции, имеющая большой коэффициент усиления, решает проблему обработки слабых сигналов, в то время как области с падающим усилением на положительном и отрицательном концах подходят для больших возбуждений. Таким образом, нейрон функционирует с большим усилением в широком диапазоне уровня входного сигнала.
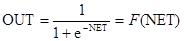 .
.
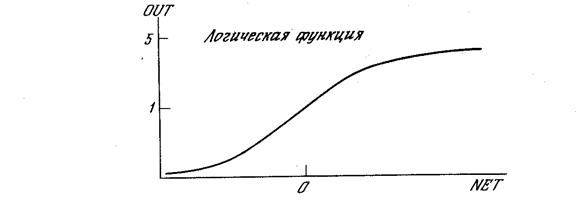
Рис. 1.4а. Сигмоидальная логистическая функция
Другой широко используемой активационной функцией является гиперболический тангенс. По форме она сходна с логистической функцией и часто используется биологами в качестве математической модели активации нервной клетки. В качестве активационной функции искусственной нейронной сети она записывается следующим образом:
OUT = th(x).
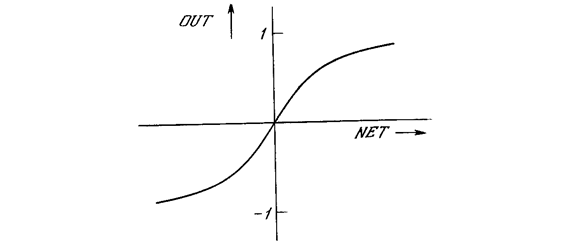
Рис. 1.4б. Функция гиперболического тангенса
Подобно логистической функции гиперболический тангенс является S-образной функцией, но он симметричен относительно начала координат, и в точке NET = 0 значение выходного сигнала OUT равно нулю (см. рис. 1.4б). В отличие от логистической функции гиперболический тангенс принимает значения различных знаков, что оказывается выгодным для ряда сетей (см. гл. 3).
Рассмотренная простая модель искусственного нейрона игнорирует многие свойства своего биологического двойника. Например, она не принимает во внимание задержки во времени, которые воздействуют на динамику системы. Входные сигналы сразу же порождают выходной сигнал. И, что более важно, она не учитывает воздействий функции частотной модуляции или синхронизирующей функции биологического нейрона, которые ряд исследователей считают решающими.
Несмотря на эти ограничения, сети, построенные из этих нейронов, обнаруживают свойства, сильно напоминающие биологическую систему. Только время и исследования смогут ответить на вопрос, являются ли подобные совпадения случайными или следствием того, что в модели верно схвачены важнейшие черты биологического нейрона.
