Ответ: б (определение)
Тренировочный тест №1
1. Какие из перечисленных операций можно ввести для трех векторов? а) сложение; б) скалярное произведение; в) векторное произведение; г) смешанное произведение.
Ответ: а, г:
а) Сложение трех векторов мы можем ввести на базе сложения двух векторов. То есть сначала находим сумму двух векторов, а затем получившийся вектор прибавляем к третьему;
б) Нет (стр 30 Замечание)
в) Нет (стр 42 пример 1.22)
г) Смешанное произведение применяется всегда для трех векторов.
---------------------------------------------------------------------------------------------------------------------
2. Какие из перечисленных равенств справедливы для любого вектора 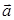 ? а)
? а) 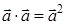 ; б)
; б) 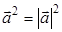 ; в)
; в) 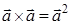 ; г)
; г) 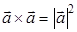 ; д)
; д) 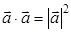 .
.
Ответ: а, б, д:
а) Да (стр. 29 п. 1°)
б) Да (стр. 29 п. 1°)
в) Нет, по формуле скалярного произведения 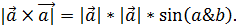 В нашем случае угол между векторами равен 0 (так как это один и тот же вектор), а значит и синус равен 0. То есть никак не равен квадрату его модуля
В нашем случае угол между векторами равен 0 (так как это один и тот же вектор), а значит и синус равен 0. То есть никак не равен квадрату его модуля
г) Нет (смотри в)
д) Да (стр. 29 п. 1°)
---------------------------------------------------------------------------------------------------------------------
3. Какие из перечисленных равенств справедливы для любых векторов 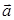 и
и 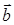 ?
?
а) 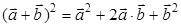 ; б)
; б) 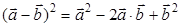 ; в)
; в) 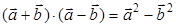 ;
;
г) 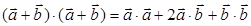 ; д)
; д) 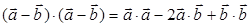 ;
;
е) 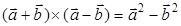 ; ж)
; ж) 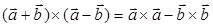 ;
;
з) 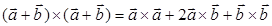 ; и)
; и) 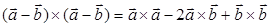 .
.
Ответ: а, б, в, г, д:
а) Да (стр. 30 пример 1.11)
б) Да (стр. 31 упражнение 1.3)
в) Да (стр. 31 упражнение 1.3)
г) Да (стр. 29 п. 1°, стр. 30 пример 1.11). Мы можем вектор а+b заменить на какой-нибудь другой вектор с и тогда получим квадрат вектора
д) Да (стр. 29 п. 1°, стр. 31 упражнение 1.3). Мы можем вектор а-b заменить на какой-нибудь другой вектор с и тогда получим квадрат вектора
е) Нет, так как слева равенства у нас вектор, а справа число
ж) Нет, так как в правой части ноль (смотри задание 2 пункт в)
з) Нет, так как слева это векторное произведение двух ОДИНАКОВЫХ векторов, а оно равно 0 (смотри задание 2 пункт в), а в правой части останется двойное векторное произведение
и) Нет (смотри пункт з)
---------------------------------------------------------------------------------------------------------------------
4. Какие из перечисленных равенств справедливы для любых векторов 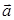 и
и 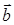 ? а)
? а) 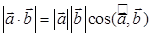 ; б)
; б) 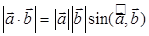 ; в)
; в) 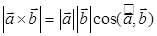 ; г)
; г) 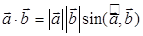 ; д)
; д) 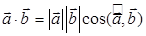 ; е)
; е) 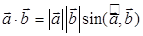 ; ж)
; ж) 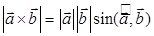 ; з)
; з) 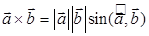 .
.
Ответ: ж, д:
а) Нет, так как число слева всегда больше нуля (так как модуль), а справа синус может быть отрицательный
б) Нет (смотри пункт а)
в) Нет, ведь мы уже знаем, что там не синус, а косинус (смотри пункт ж)
г) Нет, по формуле косинус
д) А вот это уже наш случай (стр. 29 определение)
е) не вижу разницы от пункта г
ж) Да (стр. 35 п. 1*)
з) Нет, слева вектор, а справа число
---------------------------------------------------------------------------------------------------------------------
5. Какие из перечисленных утверждений верны? а) любые сонаправленные векторы коллинеарны; б) любые противонаправленные векторы коллинеарны; в) любые коллинеарные векторы сонаправлены; г) любые коллинеарные векторы противонаправлены; д) если из двух векторов один нулевой, то эти векторы коллинеарны; е) если два вектора коллинеарны, то один из них нулевой; ж) если из трех векторов два коллинеарны, то эти три вектора компланарны; з) если три вектора компланарны, то два из них коллинеарны; и) любые два вектора компланарны; к) любые четыре вектора некомпланарны; л) можно подобрать два вектора так, что они будут некомпланарными; м) если три вектора компланарны, то один из них нулевой.
Ответ: а, б, д, ж, и:
а) и б) Без комментариев (определение)
в) Могут быть противонаправлены
г) Могут быть сонаправлены
д) Без комментариев (определение)
е) Совсем не всегда (ошибка без комментариев)
ж) Да, т.к два всегда компланарны а плоскость можем выбрать, что бы и третий был компланарен
з) Совсем не всегда (ошибка без комментариев)
и) Да
к) Совсем не всегда (ошибка без комментариев)
л) Нет
м) Совсем не всегда (ошибка без комментариев)
---------------------------------------------------------------------------------------------------------------------
6. Какие из перечисленных утверждений верны? а) если один из двух векторов нулевой, то их скалярное произведение равно нулю; б) если скалярное произведение векторов равно нулю, то один из них нулевой; в) если один из двух векторов нулевой, то их векторное произведение; г) если векторное произведение двух векторов равно нулевому вектору, то один из них нулевой.
Ответ: а, в:
а) Да (стр. 29 определение)
б) Не обязательно. К примеру, просто косинус угла между векторами может оказаться равен 0, а это не означает что вектор нулевой
в) P.S. Возможно они забыли дописать «… равно нулевому вектору». Если так и есть, то тогда да, верно (стр. 35 определение)
г) Не обязательно. К примеру, просто синус угла между векторами может оказаться равен 0, а это не означает что вектор нулевой
---------------------------------------------------------------------------------------------------------------------
7. Критерием ортогональности векторов является: а) равенство нулю их векторного произведения; б) равенство нулю их скалярного произведения; в) равенство нулю их смешанного произведения; г) пропорциональность координат; д) другой ответ.
Ответ: б (определение)
---------------------------------------------------------------------------------------------------------------------
8. Критерием коллинеарности векторов является: а) равенство нулю их векторного произведения; б) равенство нулю их скалярного произведения; в) равенство нулю их смешанного произведения; г) пропорциональность координат; д) другой ответ.
