Интерференция поляризованного света. 1. При наложении двух когерентных лучей, поляризованных во взаимно перпендикулярных

1. При наложении двух когерентных лучей, поляризованных во взаимно перпендикулярных направлениях, никакой интерферен­ционной картины получиться не может. Это доказано в опыте Френеля – Араго. Вывод из опыта:

Интерференция возникает только в том случае, если колебания во взаимодействую­щих лучах совершаются вдоль одного и того же направления.

2. Рассмотрим, что полу­чается при наложении вы­шедших из кристалличес­кой пластинки обыкновен­ного и необыкновенного лучей. Пусть пластинка вырезана параллельно оп­тической оси. При нормальном падении света на пластинку обык­новенный и необыкновенный лучи будут распространяться не разделяясь, но с различ­ными скоростями.

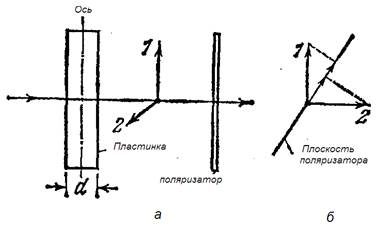
Рис.8-12

За время прохождения через пластинку между лучами возникнет разность хода

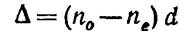(8-1)

или разность фаз

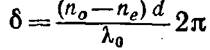(8-2)

(d — толщина, пластинки, λ₀ - длина волны в вакууме).

Если пропустить естественный свет через выре­занную параллельно оптической оси кристаллическую пластинку (рис. 8-12а), тоиз пластинки выйдут два поляризованных во вза­имно перпендикулярных плоскостях луча 1 и 2, между которыми будет существовать разность фаз, определяемая формулой (8-1). Интерферировать эти лучи не будут. Надо получить лучи с одинаковыми направлениями колебаний. Поэтому поставим на пути этих лучей поляризатор. Колебания обоих лучей после прохождения через поляризатор будут лежать в одной плоскости. Амплитуды их будут равны составляющим амплитуд лу­чей 1 и 2 в направлении плоскости поляризатора (рис. 8-2 б).

Вышедшие из поляризатора лучи 1 и 2, которые возникают из естественного света, не дают интерференции, так какони содержат в основном колебания, принадлежащие разным цугам волн, испускаемых отдельными атомами.

Если на кристаллическую пластинку падает плоскополяризованный свет, то . колебания каждого цуга разделяются между обыкновенным и необыкновенным лучами. Поэтому лучи и лучи 1 и 2, оказываются коге­рентными и будут интерферировать.

3. Рассмотрим кристаллическую пластинку, вырезанную парал­лельно оптической оси, толщина которой удовлетворяет специальным условиям. Пластинка, для которой

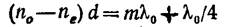
(m - любое целое число либо нуль), называется пластинкой в четверть волны. При прохождении через такую пластинку обыкновенный и необыкновенный лучи приобретают разность фаз π/2+2πm

Пластинка, для которой

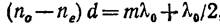
называется пластинкой в полволны:

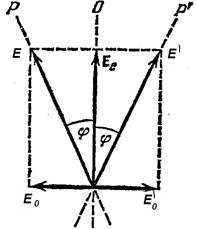
Рис.8-13

После прохождения пластинки в полволны разность фаз между колебаниями Е₀ и Е. изменяется на π (Е₀ переходит Е`₀). Поэтому пластинка в полволны поворачивает плоскость колебаний прошедшего через нее света на угол 2φ.