Лекция 2. Системы координат. Скалярные и векторные величины
ОСНОВЫ ЛИНЕЙНОЙ И ВЕКТОРНОЙ АЛГЕБРЫ
Лекция 1. Матрицы и определители.
План лекции
1.1. Матрицы, основные определения.
1.2. Действия над матрицами.
1.3. Элементарные преобразования матрицы. Ранг матрицы.
1.4. Определение определителя квадратной матрицы.
1.5. Свойства определителей.
1.6. Миноры и алгебраические дополнения. Вычисление определителя 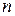 -го порядка.
-го порядка.
1.7. Метод окаймляющих миноров для вычисления ранга матрицы.
1.1
Матрицейназывается прямоугольная таблица, состоящая из 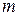 строк и
строк и 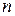 столбцов, составленная из чисел или каких-либо других объектов. Матрицы обозначаются
столбцов, составленная из чисел или каких-либо других объектов. Матрицы обозначаются
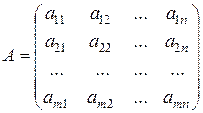 , (1.1)
, (1.1)
или коротко
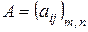 . (1.
. (1. 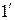 )
)
Отдельные члены матрицы называются её элементами, они обозначаются 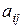 , где
, где 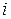 - номер строки,
- номер строки, 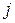 - номер столбца (
- номер столбца ( 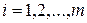 ;
; 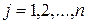 ), в которых находится этот элемент. Каждая матрица имеет определенные размеры, т.е. количество строк и столбцов матрицы. Если
), в которых находится этот элемент. Каждая матрица имеет определенные размеры, т.е. количество строк и столбцов матрицы. Если 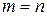 , то матрица называется квадратной, тогда говорят о её порядке. Матрица, у которой всего один столбец (строка), называется - матрицей-столбцом (матрицей-строкой). Матрица, у которой все элементы равны нулю, называется нулевой и обозначается
, то матрица называется квадратной, тогда говорят о её порядке. Матрица, у которой всего один столбец (строка), называется - матрицей-столбцом (матрицей-строкой). Матрица, у которой все элементы равны нулю, называется нулевой и обозначается 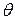 . Квадратная матрица, у которой равны нулю все элементы, кроме стоящих на главной диагонали, называется диагональной. Диагональная матрица, у которой все диагональные элементы равны 1, называется единичной и обозначается
. Квадратная матрица, у которой равны нулю все элементы, кроме стоящих на главной диагонали, называется диагональной. Диагональная матрица, у которой все диагональные элементы равны 1, называется единичной и обозначается 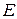 . Если в матрице
. Если в матрице 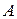 поменять местами строки со столбцами, то получим матрицу
поменять местами строки со столбцами, то получим матрицу 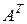 , которая называется транспонированной. Матрица, совпадающая со своей транспонированной, называется симметрической.
, которая называется транспонированной. Матрица, совпадающая со своей транспонированной, называется симметрической.
Две матрицы 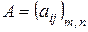 и
и 
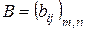 одинакового размера равны, если равны их соответствующие элементы, т.е.
одинакового размера равны, если равны их соответствующие элементы, т.е. 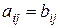 для
для 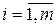 ,
, 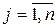 .
.
1.2
Рассмотрим операции над матрицами. Многие арифметические операции с матрицами логически вытекают из аналогичных операций со скалярными величинами.
Суммойдвух матриц 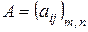 и
и 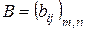 называется матрица
называется матрица 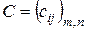 , каждый элемент которой равен сумме соответствующих элементов матриц
, каждый элемент которой равен сумме соответствующих элементов матриц 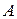 и
и 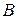 , т.е.
, т.е. 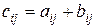 , где
, где 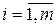 ,
, 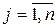 .
.
Замечание. Складывать можно лишь те матрицы, которые имеют одинаковые размеры.
Пример 1. Пусть матрица  характеризует заболеваемость учеников гриппом и ОРВИ в 10 А классе в зимние месяцы, а матрица
характеризует заболеваемость учеников гриппом и ОРВИ в 10 А классе в зимние месяцы, а матрица  характеризует заболеваемость учеников гриппом и ОРВИ в 10 Б классе в этот же период. Причем строки матриц – характеризуют число заболевших по месяцам, а столбцы матриц – число заболевших соответственно гриппом и ОРВИ
характеризует заболеваемость учеников гриппом и ОРВИ в 10 Б классе в этот же период. Причем строки матриц – характеризуют число заболевших по месяцам, а столбцы матриц – число заболевших соответственно гриппом и ОРВИ
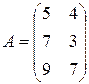 и
и 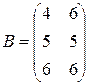 .
.
Складывая эти матрицы, получим третью матрицу 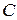 , характеризующую заболеваемость в 10-х классах:
, характеризующую заболеваемость в 10-х классах:
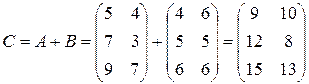 .
.
Произведением матрицы 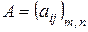 на число
на число 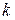 называется такая матрица
называется такая матрица 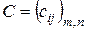 , каждый элемент которой равен произведению соответствующего элемента матрицы
, каждый элемент которой равен произведению соответствующего элемента матрицы 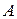 на число
на число 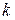 , т.е.
, т.е. 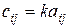 ,
, 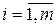 ,
, 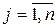 .
.
Пример 2. Пусть среднее количество, продаваемых в аптеке в день шприцев, отражено в матрице 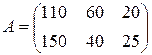 . Первый столбец характеризует продажу шприцев по 2 мл, второй по 5 мл, третий столбец по 10 мл. Первая строка продажу шприцев отечественного производства, а вторая строка – импортного производства. Тогда матрица
. Первый столбец характеризует продажу шприцев по 2 мл, второй по 5 мл, третий столбец по 10 мл. Первая строка продажу шприцев отечественного производства, а вторая строка – импортного производства. Тогда матрица 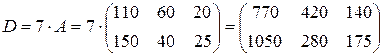 будет характеризовать недельный уровень продаж каждого из видов шприцев.
будет характеризовать недельный уровень продаж каждого из видов шприцев.
Произведением матрицы 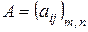 на матрицу
на матрицу 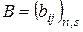 называется такая матрица
называется такая матрица 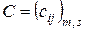 , у которой каждый элемент
, у которой каждый элемент 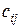 равен сумме парных произведений элементов
равен сумме парных произведений элементов 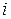 -той строки матрицы
-той строки матрицы 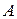 на соответствующие элементы
на соответствующие элементы 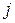 -того столбца матрицы
-того столбца матрицы  , т.е.
, т.е.
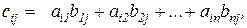
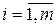 ,
,  .
.
Замечание 1. Произведение матриц 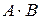 существует только в том случае, если число столбцов матрицы
существует только в том случае, если число столбцов матрицы 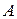 равно числу строк матрицы
равно числу строк матрицы 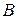 .
.
Замечание 2. Произведение матриц не коммутативно (не выполняется перестановочный закон умножения).
Пример 3. Средства на вакцинацию населения перечисляются страховой компанией. Пусть в матрице 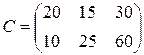 первая строка характеризует потребность поликлиники в вакцинах в сентябре, вторая строка – потребность в вакцинах в октябре, первый столбец – количество доз вакцины против столбняка, второй столбец – количество доз вакцины против кори, третий столбец – количество доз вакцины против гриппа. В матрице
первая строка характеризует потребность поликлиники в вакцинах в сентябре, вторая строка – потребность в вакцинах в октябре, первый столбец – количество доз вакцины против столбняка, второй столбец – количество доз вакцины против кори, третий столбец – количество доз вакцины против гриппа. В матрице 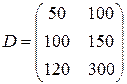 первый столбец характеризует стоимость вакцинации, а второй столбец – стоимость вакцин; первая строка характеризует затраты на вакцинацию против столбняка, вторая строка – против кори, третья строка – против гриппа. Тогда
первый столбец характеризует стоимость вакцинации, а второй столбец – стоимость вакцин; первая строка характеризует затраты на вакцинацию против столбняка, вторая строка – против кори, третья строка – против гриппа. Тогда
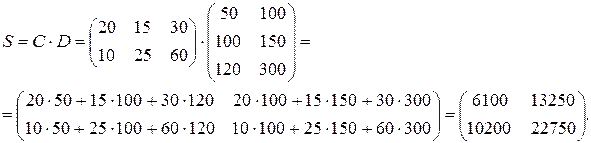
Таким образом, в матрице 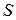 элемент 6100 - стоимость вакцинации в сентябре, 10200 - стоимость вакцинации в октябре, 13250 – стоимость вакцин, необходимых для вакцинации населения в сентябре, 22750 - стоимость вакцин в октябре.
элемент 6100 - стоимость вакцинации в сентябре, 10200 - стоимость вакцинации в октябре, 13250 – стоимость вакцин, необходимых для вакцинации населения в сентябре, 22750 - стоимость вакцин в октябре.
1.3
Матрица 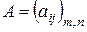 называется матрицей ступенчатого вида, если все элементы, стоящие ниже главной диагонали, равны нулю, т.е.
называется матрицей ступенчатого вида, если все элементы, стоящие ниже главной диагонали, равны нулю, т.е. 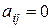 для всех
для всех 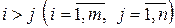 .
.
Рангом матрицы назовем число ненулевых строк в матрице, сведенной к ступенчатому виду. Для матрицы А ранг матрицы обозначают rang A.
Для приведения матрицы к ступенчатому виду применяют элементарные преобразования матрицы, к числу которых относят следующие.
1. Перестановка любых строк матрицы.
2. Прибавление к одной строке элементов другой строки.
3. Умножение всех элементов одной строки матрицы на число 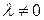 .
.
4. Прибавление к одной строке другой строки, умноженной на число 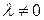 .
.
5. Вычеркивание нулевой строки.
6. Вычеркивание из двух или нескольких равных строк всех кроме одной.
7. Вычеркивание из двух или нескольких пропорциональных строк всех кроме одной.
Замечание 1. Элементарные преобразования матрицы можно проводить не только над строками, но и над столбцами.
Замечание 2. Иногда говорят о ранге матрицы по строкам и о ранге матрицы по столбцам, причем доказывают их равенство, и далее говорят просто о ранге матрицы.
Пример 4. Найти ранг матрицы:
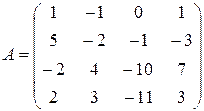 .
.
Решение. Сводим матрицу к ступенчатому виду:
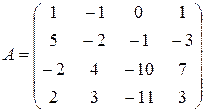 ~*)
~*)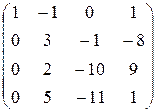 ~ **)
~ **)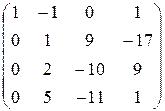 ~
~
~ ***)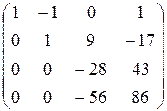 ~ ****)
~ ****) 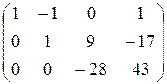 .
.
При сведении матрицы к ступенчатому виду выполнялись следующие элементарные преобразования матрицы:
*) первую строку матрицы умножали на -5, 2, -2 и прибавляли соответственно ко второй, третьей, четвёртой строке матрицы;
**) третью строку умножали на -1 и прибавляли ко второй строке;
***) вторую строку умножали на -2, на -5 и прибавляли соответственно к третьей и к четвёртой строке;
****) вычеркнули четвёртую строку, так как она пропорциональна третьей строке.
В результате перечисленных элементарных преобразований матрица свелась к ступенчатому виду. Таким образом, 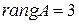 .
.
1.4
Рассмотрим квадратную матрицу второго порядка
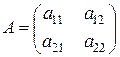 .
.
Определителем второго порядка, соответствующим матрице 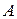 , называется число, равное
, называется число, равное 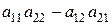 . Определитель обозначают
. Определитель обозначают
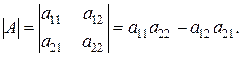 (1.2)
(1.2)
Элементы матрицы 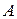 называются элементами определителя
называются элементами определителя 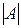 , элементы
, элементы 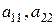 образуют главную диагональ, а элементы
образуют главную диагональ, а элементы 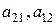 - побочную.
- побочную.
Рассмотрим квадратную матрицу третьего порядка 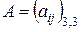 . Определителем третьего порядка, соответствующим матрице
. Определителем третьего порядка, соответствующим матрице 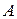 , называется число, равное
, называется число, равное
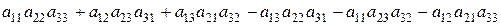 и обозначаемое символом
и обозначаемое символом 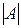 , т.е.
, т.е.
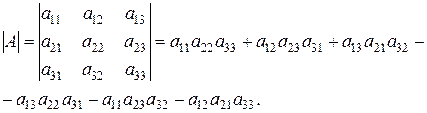 (1.3)
(1.3)
Чтобы запомнить, какие произведения в правой части равенства (1.3) брать со знаком «+», какие - со знаком «минус», полезно правило, называемое правилом треугольника (рис. 1.1).

Рисунок 1.1.Правило треугольника.
Каждое произведение с указанным знаком, входящее в (1.3), называется членом определителя. Среди входящих в произведение элементов имеются представители от каждой строки и от каждого столбца. Эти элементы можно в каждом члене расположить в порядке возрастания первого индекса, как и сделано в (1.3). Тогда номера столбцов в каждом члене определителя представляют собой всевозможные перестановки из чисел 1, 2, 3. При этом перестановку 1, 2, 3 называют основной. Говорят, что в перестановке произведена транспозиция двух определенных её элементов, если эти элементы заменены местами. Перестановка называется четной(нечетной), если она получается из основной перестановки при помощи четного (нечетного) числа транспозиций.
Пусть дана перестановка 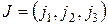 , где
, где 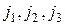 , это числа 1, 2, 3, взятые в некотором порядке. Число транспозиций, с помощью которых можно получить эту перестановку из основной перестановки, обозначим через
, это числа 1, 2, 3, взятые в некотором порядке. Число транспозиций, с помощью которых можно получить эту перестановку из основной перестановки, обозначим через 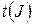 . Теперь можно дать другое эквивалентное (1.3) определение определителя третьего порядка.
. Теперь можно дать другое эквивалентное (1.3) определение определителя третьего порядка.
Определителем третьего порядка называется число 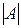 , равное алгебраической сумме всевозможных произведений вида
, равное алгебраической сумме всевозможных произведений вида 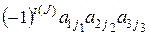 , где
, где 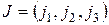 - всевозможные перестановки основной перестановки 1, 2, 3, т.е.
- всевозможные перестановки основной перестановки 1, 2, 3, т.е.
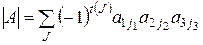 . (1.4)
. (1.4)
Данное определение можно распространить и на случай определителя 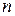 -го порядка.
-го порядка.
Определителем n-го порядканазывается число
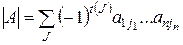 , (1.5)
, (1.5)
равное алгебраической сумме всевозможных произведений элементов определителя, взятых по одному из каждой строки и столбца, причем знак каждого произведения определяется числом 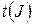 , равным числу транспозиций при переходе от основной перестановки 1, 2, ... ,
, равным числу транспозиций при переходе от основной перестановки 1, 2, ... , 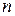 к перестановке
к перестановке 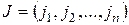 . Произведение
. Произведение 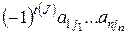 называется членом определителя.
называется членом определителя.
1.5
Укажем основные свойства определителей, которые могут быть доказаны исходя из определения определителя.
10. При транспонировании определитель не меняет своего значения.
20. Если все элементы какой - либо строки определителя равны нулю, то определитель равен нулю.
30. Если в определителе поменять местами две какие-либо строки, то абсолютная величина определителя не изменится, а знак изменится на противоположный.
40. Определитель, содержащий две равные строки, равен нулю.
50. Если все элементы какой-нибудь строки определителя умножить на число 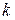 , то значение определителя изменится в
, то значение определителя изменится в 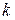 раз.
раз.
60. Определитель, содержащий две пропорциональные строки, равен нулю.
70. Если одна из строк определителя есть линейная комбинация других строк, то определитель равен нулю.
80. Определитель не меняет своего значения, если к элементам одной из его строк прибавить линейную комбинацию других строк.
Замечание. Исходя из свойства 10 свойства 20- 80 остаются справедливы и для столбцов.
Отмеченные свойства определителей используются при их вычислении.
1.6
Миноромкакого-либо элемента определителя называется определитель, полученный из данного вычеркиванием той строки и того столбца, которым принадлежит этот элемент. Минор элемента 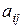 обозначается
обозначается 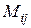 .
.
Алгебраическим дополнениемэлемента 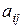 определителя называется минор этого элемента, взятый со знаком
определителя называется минор этого элемента, взятый со знаком 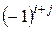 . Алгебраическое дополнение элемента
. Алгебраическое дополнение элемента 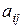 обозначается
обозначается 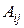 , т.е.
, т.е. 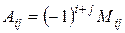 .
.
На практике для вычисления определителей может быть применена следующая теорема.
Теорема.Определитель равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения, т.е. для определителя 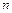 -го порядка имеем:
-го порядка имеем:
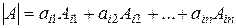 . (1.6)
. (1.6)
Формула (1.6) называется разложением определителя 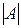 по элементам
по элементам 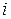 -той строки.
-той строки.
На практике обычно пользуются следствием из этой теоремы.
Следствие.Если все элементы какой-либо строки (столбца) определителя равны нулю кроме одного, то определитель равен произведению этого ненулевого элемента на его алгебраическое дополнение.
Замечание.К виду, указанному в следствии, определитель приводят с помощью свойства 80 определителя.
Пример 5. Вычислить определитель матрицы 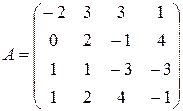 .
.
Решение.
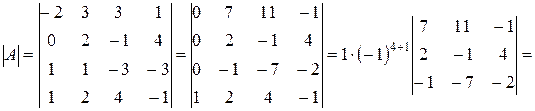
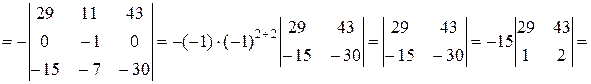
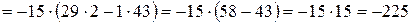 .
.
Замечание 1. При переходе ко второму определителю четвёртую строку умножали на 2 и на -1 и добавляли соответственно к первой и третьей строкам определителя.
Замечание 2. 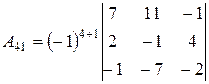 - алгебраическое дополнение элемента, стоящего в четвёртой строке и первом столбце, т.е.
- алгебраическое дополнение элемента, стоящего в четвёртой строке и первом столбце, т.е. 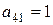 .
.
Замечание 3. Далее при вычислении определителя 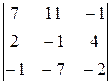 с помощью второго столбца получали нули во второй строке, умножая этот столбец на 2 и на 4 и добавляя соответственно к первому и третьему столбцам.
с помощью второго столбца получали нули во второй строке, умножая этот столбец на 2 и на 4 и добавляя соответственно к первому и третьему столбцам.
Замечание 4. 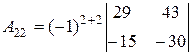 - алгебраическое дополнение элемента
- алгебраическое дополнение элемента 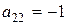 , стоящего во второй строке и втором столбце определителя третьего порядка.
, стоящего во второй строке и втором столбце определителя третьего порядка.
Замечание 5. Определитель 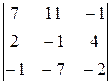 можно было раскрыть по правилу треугольника:
можно было раскрыть по правилу треугольника:
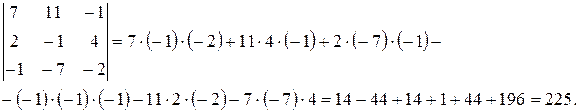
Следовательно, вновь получаем 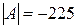 .
.
1.7
Строки (столбцы) матрицыназываются линейно зависимыми, если одна (один) из них есть линейная комбинация других. В противном случае строки (столбцы) матрицы называются независимыми. Несложно заметить, что в матрице, сведенной к ступенчатому виду, строки линейно независимы. Исходя из этого, можно дать другое определение ранга матрицы.
Рангом матрицыназывается число линейно независимых строк (столбцов) этой матрицы.
Другой способ вычисления ранга матрицы основан на следующих свойствах:
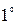 . Определитель квадратной матрицы равен нулю тогда и только тогда, когда его строки (столбцы) линейно зависимы.
. Определитель квадратной матрицы равен нулю тогда и только тогда, когда его строки (столбцы) линейно зависимы.
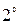 . Если у определителя все миноры
. Если у определителя все миноры 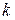 -го порядка равны нулю, то и все миноры более высокого порядка тоже равны нулю.
-го порядка равны нулю, то и все миноры более высокого порядка тоже равны нулю.
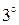 . Наивысший порядок отличных от нуля миноров матрицы равен рангу этой матрицы.
. Наивысший порядок отличных от нуля миноров матрицы равен рангу этой матрицы.
Метод определения ранга матрицы, основанный на свойстве 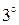 носит название метода окаймляющих миноров. Для нахождения ранга этим методом
носит название метода окаймляющих миноров. Для нахождения ранга этим методом
– находят элемент в матрице, отличный от нуля. Это есть минор 1-го порядка.
– окаймляют выделенный минор, добавляя какой-либо столбец и какую-либо строку.
– если окаймляющий минор отличен от нуля, то переходят к окаймляющему минору следующего порядка.
– если окаймляющий минор равен нулю, то находят другое окаймление минора предыдущего порядка.
– если был найден минор 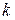 -го порядка, отличный от нуля, а все окаймляющие его миноры
-го порядка, отличный от нуля, а все окаймляющие его миноры 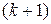 -го порядка равны нулю, то ранг матрицы равен
-го порядка равны нулю, то ранг матрицы равен 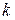 .
.
Пример 6. С помощью метода окаймляющих миноров найти ранг матрицы
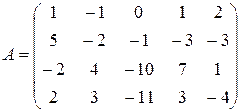 .
.
Решение. Находим ненулевой минор 1-го порядка. Начнем с левого верхнего угла: 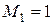 .
.
Окаймляем его, добавляя 2-ю строку и 2-ой столбец:
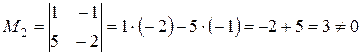 .
.
Окаймляем минор 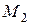 . Добавим 3-ю строку и 3-й столбец:
. Добавим 3-ю строку и 3-й столбец:
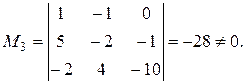
Окаймляем минор 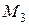 . Добавим 4-ю строку и 4-й столбец:
. Добавим 4-ю строку и 4-й столбец:
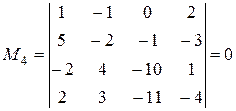 .
.
Составляем другое окаймление минора 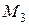 . Добавляем к ненулевому минору третьего порядка 4-ю строку и 5-ый столбец:
. Добавляем к ненулевому минору третьего порядка 4-ю строку и 5-ый столбец:
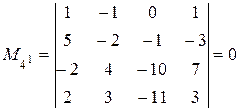 .
.
Так как все окаймляющие миноры 4-го порядка равны нулю, то наивысший порядок отличных от нуля миноров равен 3. Следовательно, 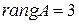 .
.
Лекция 2. Системы координат. Скалярные и векторные величины.
План лекции
2.1. Прямоугольные декартовы координаты на плоскости и в пространстве. Основные задачи на прямоугольные координаты.
2.2. Полярная система координат, ее связь с прямоугольной. Цилиндрическая и сферическая системы координат.
2.3. Скаляры и векторы, основные определения. Линейные действия над векторами.
2.4. Линейная зависимость системы векторов, базис и ранг системы векторов, координаты вектора.
2.5. Скалярное произведение двух векторов, длина вектора, угол между векторами, условие ортогональности.
2.6. Векторное произведение векторов, его приложения.
2.7. Смешанное произведение векторов, его приложения.
2.1
Одним из важных вопросов математики является определение положения точки.
Координатной прямой называется прямая, на которой выбрано начало отсчета, положительное направление и единица масштаба.
Как известно, между точками координатной (числовой) прямой и множеством действительных чисел существует взаимно-однозначное соответствие. Поэтому положение точки на прямой полностью определяется одним числом – координатой точки. Для определения положения точки на плоскости необходимо ввести систему координат на плоскости. Это можно сделать многими способами, один из которых – построение прямоугольной декартовой системы координат.
Возьмем на плоскости две взаимно перпендикулярные прямые 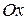 и
и 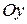 с указанными на них положительными направлениями и единицей масштаба (рисунок 2.1). Прямые
с указанными на них положительными направлениями и единицей масштаба (рисунок 2.1). Прямые 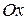 и
и 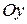 называются координатными осями, причем
называются координатными осями, причем 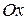 - ось абсцисс,
- ось абсцисс, 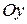 - ось ординат, точка их пересечения называется началом координат. Координатные оси
- ось ординат, точка их пересечения называется началом координат. Координатные оси 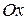 и
и 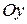 с выбранной единицей масштаба называются прямоугольной декартовой системой координат на плоскости. Произвольной точке
с выбранной единицей масштаба называются прямоугольной декартовой системой координат на плоскости. Произвольной точке 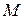 плоскости поставим в соответствие два числа:
плоскости поставим в соответствие два числа:
абсциссу 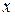 , равную расстоянию от точки
, равную расстоянию от точки 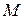 до оси
до оси 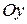 , взятому со знаком «+», если
, взятому со знаком «+», если 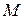 лежит правее
лежит правее 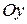 , и со знаком «-», если
, и со знаком «-», если 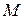 лежит левее
лежит левее 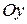 ;
;
ординату 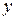 , равную расстоянию от точки
, равную расстоянию от точки 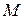 до оси
до оси 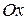 , взятому со знаком «+», если
, взятому со знаком «+», если 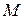 лежит выше
лежит выше 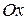 , и со знаком «-», если
, и со знаком «-», если 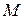 лежит ниже
лежит ниже 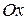 .
.
Абсцисса 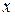 и ордината
и ордината 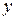 называются прямоугольными декартовыми координатами точки
называются прямоугольными декартовыми координатами точки 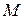 . Записывают
. Записывают 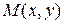 .
.
Между точками плоскости и упорядоченными парами чисел 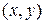 - их координатами существует взаимно-однозначное соответствие: каждой точке плоскости соответствует единственная пара действительных чисел
- их координатами существует взаимно-однозначное соответствие: каждой точке плоскости соответствует единственная пара действительных чисел 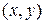 и, обратно, каждой паре действительных чисел
и, обратно, каждой паре действительных чисел 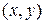 соответствует единственная точка плоскости.
соответствует единственная точка плоскости.
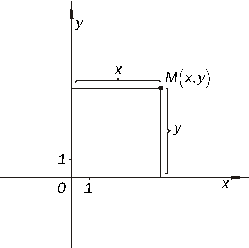
Рисунок 2.1. Прямоугольная система координат на плоскости.
Аналогичным образом вводим понятие прямоугольной декартовой системы координат в пространстве.
Возьмем в трёхмерном пространстве три взаимно перпендикулярные прямые 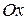 ,
, 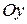 ,
, 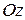 с общим началом, укажем на них положительные направления и единицу масштаба. Такая система называется прямоугольной декартовой системой координат в пространстве (Рисунок 2.2). Оси
с общим началом, укажем на них положительные направления и единицу масштаба. Такая система называется прямоугольной декартовой системой координат в пространстве (Рисунок 2.2). Оси 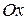 ,
, 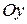 ,
, 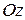 называются соответственно осью абсцисс, осью ординат и осью аппликат.
называются соответственно осью абсцисс, осью ординат и осью аппликат.
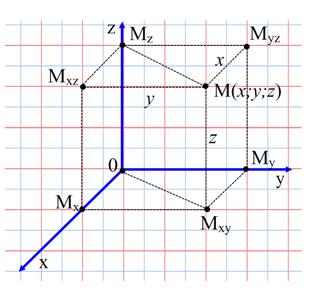
Рисунок 2.2. Прямоугольная система координат в пространстве
Положение любой точки 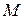 пространства можно охарактеризовать с помощью трёх чисел – абсциссы
пространства можно охарактеризовать с помощью трёх чисел – абсциссы 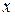 , ординаты
, ординаты 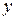 , аппликаты
, аппликаты 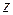 , которые равны расстоянию (взятому с определённым знаком) от точки
, которые равны расстоянию (взятому с определённым знаком) от точки 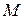 до координатных плоскостей
до координатных плоскостей 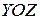 ,
, 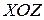 ,
, 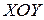 . На рисунке 2.2
. На рисунке 2.2 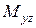 проекция точки
проекция точки 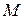 на плоскость
на плоскость 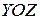 ,
, 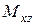 - проекция точки
- проекция точки 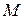 на плоскость
на плоскость 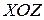 ,
, 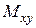 - проекция точки
- проекция точки 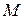 на плоскость
на плоскость 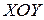 ;
; 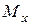 и
и 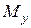 проекции, например, точки
проекции, например, точки 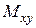 в плоскости
в плоскости 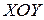 на координатные оси
на координатные оси 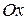 и
и 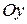 ,
, 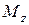 - проекция, например, точки
- проекция, например, точки 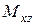 в плоскости
в плоскости 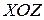 на координатную ось
на координатную ось 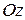 . Тогда по определению
. Тогда по определению 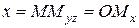 ,
, 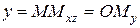 ,
, 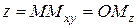 .
.
Таким образом, с помощью координат мы производим учет всех точек прямой, плоскости или пространства. Такой учет позволяет соединить в единое целое геометрию и алгебру. Каждое понятие, каждая теорема могут быть высказаны как бы на двух языках – на геометрическом и аналитическом, что позволяет переходить от оперирования геометрическим объектом к оперированию его алгебраическим заданием (уравнением, неравенством и т.п.). Решение геометрических задач аналитически (алгебраическим методом) и составляет сущность метода координат.
Рассмотрим основные задачи на прямоугольные координаты на плоскости.
