Вопрос 8. Общее уравнение прямой

Всякое уравнение 1-й степени относительно x и y (Ax+By+C=0) определяет в прямоугольной системе координат x-o-y некоторую прямую.

1. А≠0; В≠0; С≠0 Разделим всечлены уравнения на В:

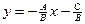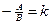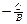; ; =b ; y=kx+b

2.A=0; B≠0; C≠0 Делим на B:

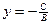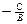; =b ; y=b

3.А≠0; B=0; С≠0

Ax+C=0 Делим на A 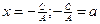; x=a

4. А≠0; В≠0; С=0 Ax+By=0 Делим на В:

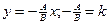; y=kx

5.A=0; В≠0; C=0 Делим на В y=0

6.А≠0; B=0; C=0 Делим на А x=0

Т.О. во всех случаях уравнение Ax+By+C=0 где A и B одновременно не равны 0 является уравнением прямой линии и это уравнение называется общим уравнением прямой. В прямоугольной системе координат всякая прямая может быть представлена уравнением первой степени и обратно.

Вопрос 9. Уравнение прямой проходящей через данную точку в данном направлении.

Необходимо составить уравнение прямой, проходящей через точку Mo (xo;yo) и имеющей угловой коэффициент К. Уравнение этой прямой можно записать как уравнение прямой с угловым коэффициентом: (1) y=kx+b, k- известно, b-?

Т.к. прямая проходящая через Mo(xo;yo), то координаты этой точки должны удовлетворять (1): yo=kxo+b (2) , b=yo-kxo, подставим b в уравнение (1):

y=kx+(yo-kxo)=> y-yo=k(x-xo) (3) В этом уравнении k-заданно, xo и yo – известны. (3) называется уравнением прямой, проходящей через данную точку в заданном направлении.

Вопрос 10. Уравнение прямой, проходящей через 2 данные точки.

Необходимо составить уравнение прямой, не вертикально проходящей через точки M1(x1,y1), M2 (x2,y2), k-? Уравнение этой прямой можно записать в виде:

y-y1=k(x-x1) (1), т.к. искомая прямая проходит через точку M2, то координаты этой точки должны удовлетворять уравнению (1) y2-y1=k(x2-x1)=>k=y2-y1/x2-x1 (5) подставим k в уравнение (1) и получим искомое уравнение прямой:

y1-y2/y2-y1=x-x1/x2-x1 – искомое уравнение. Уравнение (5) позволяет определить K по двум точкам прямой. Если y2=y1, то уравнение искомой прямой = y=y1, если x2=x1, то уравнение искомой прямой =x=x1 и ║оси ОХ.

Вопрос 11. Уравнение прямой в отрезках на осях.

Необходимо составить Ур-е прямой, если известно что на оси абсцисс она отсекает отрезок величиной а (а≠0), а на оси ординат в(в≠0). Данная прямая отсекает на ОХ отрезок ОМ, а на оси ОУ отрезок ОN , тогда точка М имеет коорд. М(а:0), а точка N(0:в). Воспользуемся уравнением прямой проходящей через две точки М и N

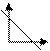Подставим корд. этих двух точек в ур-е: y-y1/y2-y1=x-x1/x2-x1;

y-0/b-0=x-a/0-a;

y/b=x-a/-a=>x/a+y/b=1 уравнение прямой в отрезках на осях.

Вопрос 12. Пересечение двух прямых.

L1:A1x+B1y+C1=0; L2: A2x+B2y+C2=0

L1и L2 заданы уравнениями. Нужно определить точку пересечения этих прямых, для этого необходимо решить систему данных ур-й: A1B1-A2B2=0, тогда система ур-й имеет единственное решение: X=B1C2-B2C1/A1B2-A2B1; Y=A2C1-A1C2/A1B2-A2B1 это значит прямые L1и L2не параллельны и пересекаются в одной точке с координатами XY.