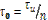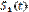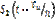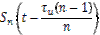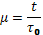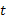Согласованный фильтр и накопление амплитуды сигнала

Приложение 1

Можно показать [3, 28], что в частотной области при неравномерном спектре аддитивного шума оптимальная комплексная передаточная функция согласованного фильтра (СФ) с сигналом s(t) равна:

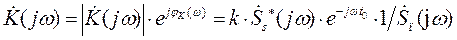, (П.1-1)

где k- const; 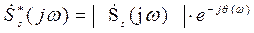- комплексная сопряженная спектру входного сигнала 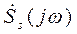спектральная плотность амплитуд (СПА); t₀ - задержка сигнала в СФ; 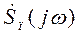- комплексная СПА шума.

В области t импульсная характеристика (ИХ) СФ g(t) = s(t₀ - t) (Рис. П.1-1) сдвинута относительно s(- t) на t₀ и зеркальна к сигналу s(t). При этомв отличие от кривой s(- t),симметричной относительно оси ординат, ИХ симметрична сигналу s(t) в точке t = t₀ /2,где задержка t₀ ≥ T_c и длительность T_c сигнала конечны.

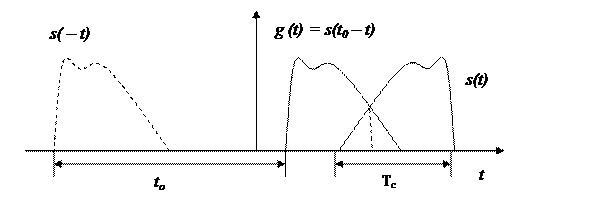Рис. П.1-1. Импульсная характеристика g(t) СФ с сигналом s(t).

СФ с параметрами (П.1-1) реализует оптимальный по критерию максимума отношения сигнал/шум (ОСШ) прием сигнала при аддитивном белом гауссовском шуме (АБГШ) с двухсторонней спектральной плотностью мощности (СПМ) 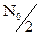, а также квазиоптимальный прием при стационарной помехе с неравномерным спектром .

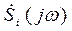Примеры построения СФ.

1. Построить СФ для приема при АБГШ прямоугольного видеоимпульса S(t) и пачки из n периодических с периодом 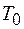видеоимпульсов.

Пусть 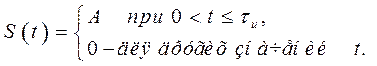(П.1-2)

Спектр видеоимпульса определен преобразованием Фурье от S(t).

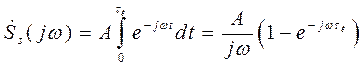. (П.1-3)

При задержке в СФ 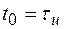, комплексный коэффициент передачи СФ (П.1-1) равен [28]:

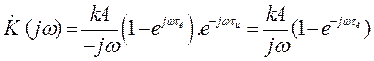, (П.1-4)

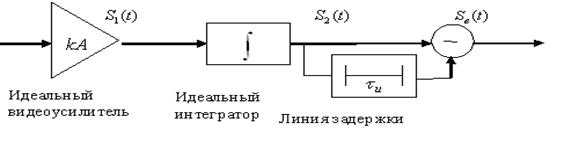который можно реализовать согласно функциональной схемы СФ рис. П.1-2, где функция 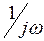реализуется интегратором, а функция 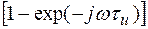→ вычитанием сигналов S₂(t) с выходов интегратора без задержки и с задержкой на .

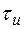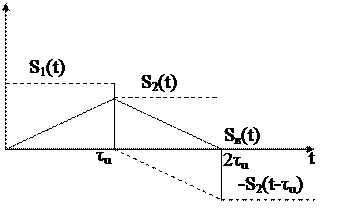
Рис. П.1-2. Функциональная схема СФ для прямоугольного видеоимпульса S(t).

Эпюры формирования напряжений в СФ: S_в(t) – АКФ сигнала S(t).

Оценим ОСШ на выходе СФ. Для этого найдем выходной сигнал СФ как ОПФ от СПА сигнала на выходе линейного СФ:

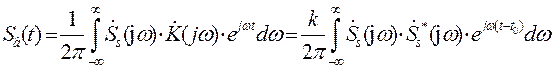.(П.1-5)

В результате при 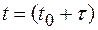этот выходной сигнал СФ определен ОПФ от СПМ сигнала 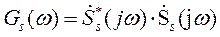, т. е. автокорреляционной функцией (АКФ) 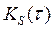входного сигнала S(t) (рис. П.1-2):

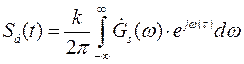
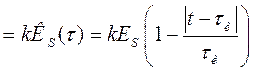(П.1-6)

где 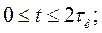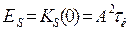-значение пика сигнала на выходе СФ, определяемое АКФ 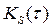входного сигнала S(t) при 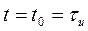, которая равна нулю при .

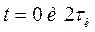Дисперсию шума на выходе СФ получим из АКФ шума на выходе СФ при 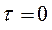, которая в свою очередь определена ОПФ от СПМ шума 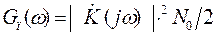на выходе линейного СФ. В результате эта дисперсия определяется также АКФ сигнала S(t) при 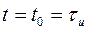и равна:

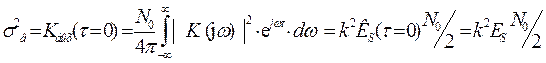. (П.1-7)

В этом случае ОСШ по напряжению S_в(t)/σ_в на выходе СФ, согласно (П.4) и (П.5), при 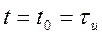равно:

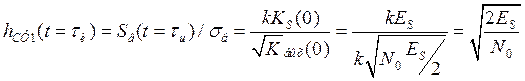. (П.1-8)

Таким образом, согласно (П.1-6) и (П.1-7) отсчеты шума на выходе СФ определяются АКФ 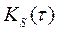входного сигнала S(t) и взятые через интервал 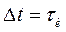являются некоррелированными. В этом случае для пачки из n импульсов, следующих с периодом 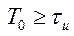, можно реализовать СФ с когерентным накоплением амплитуды для сигнала (П.1-6) в n раз и некогерентным – для шума. Для этого устанавливают на выходе или входе СФ для одиночного импульса дополнительную линию задержки (ЛЗ) на интервал nT₀ с отводами через T₀ и сумматор. При больших n на выходе СФ устанавливают рециркулятор (РЦ), т. е. рекурсивный фильтр [30]. В этом случае отсчеты шума на входе СФ будут некоррелированными и складываться в РЦ (в отличие от сигнала) по мощности.

В результате ОСШ по мощности на выходе СФ для пачки из n видеоимпульсов на основе ЛЗ и сумматорабудет в n раз больше:

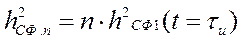(П.1-9)

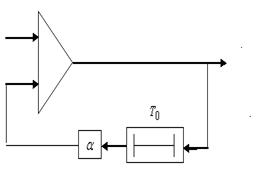
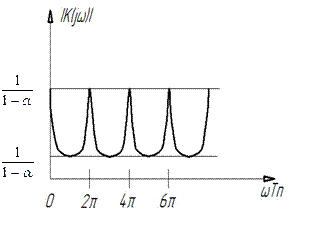
На практике бывает трудно осуществить задержку на длительность пачки импульсов и используют ЛЗ на один период повторения 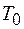с обратной связью (ОС) с выхода на вход, т. е. РЦ рис. П.1-3а), где коэффициент ОС α < 1.

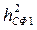
Вход РЦ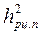

Выход РЦ

а)

б)

Рис. П.1-3: а)- Структурная схема РЦ для накопления амплитуды

n периодических импульсов с выхода СФ₁ с видеоимпульсом.

б)- АЧХ рециркулятора.

Можно показать, что ИХ 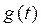РЦ для пачки из n видеоимпульсови соответствующий комплексный коэффициент передачи 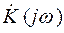(как сумма геометрической прогрессии 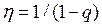) при n → ∞ имеют вид:

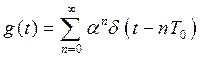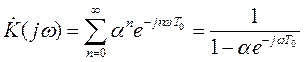, . (П.1-10)

Модуль 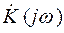РЦ, т. е. АЧХ РЦ получим (представляя 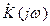в алгебраической форме (a-jb) и вычисляя 1/(a² +b² ) ) в виде:

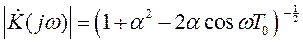(П.1-11)

АЧХ РЦ является периодической функцией частоты и имеет вид (рис. П.1-3б) гребёнки с максимумами (положительная обратная связь), равными 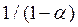при частотах 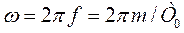, где m = 0,1,2,, и минимумами 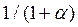при m = 1/2, 3/2 . Такие фильтры называют гребенчатыми.

Можно показать [5, 30], что ОСШ по мощности на выходе СФ для пачки из n импульсов с накоплениемна РЦ равно:

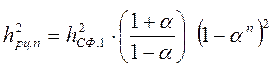, (П.1-12)

и является функцией двух переменных n и α.

При заданном значении n можно найти (дифференцированием выражения (П.1-12) по α) оптимальное значениеα,обеспечивающее максимум ОСШ, которое равно:

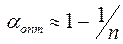(П.1-13)

Однако в таком РЦ сложно накопить 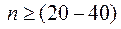импульсов, т.к. согласно (П.1-13) 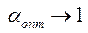, а РЦ к неустойчивости. Поэтому при большихзначениях n применяют двухэтапный последовательный накопитель на основе РЦ 1 и РЦ 2 рис. П.1-4.

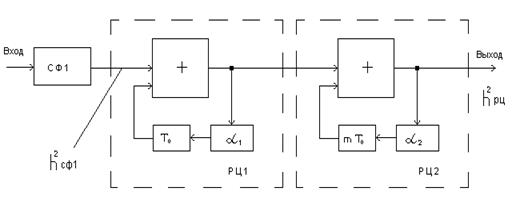
Рис. П.1-4. СФ для пачки с большим числом n импульсов

на основе двухэтапного последовательного накопителя.

Отсчеты шума на выходе РЦ 1 зависимы (как и сигнала) с большим коэффициентом корреляции 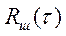, и накопление сигнала в РЦ 2 невозможно. Поэтому уменьшают 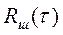путем увеличения в m раз интервала задержки в РЦ 2. В этом случае 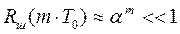и накопление шума в РЦ 2 реализуется по мощности, как и в РЦ 1, а сигналов - когерентно по амплитуде.

При заданном значении n и α существует оптимальное значение m

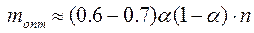, (П.1-14)

при котором выигрыш в ОСШ от накопления максимален. Например, при α=0.9 и n=100 получим 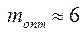, а выигрыш в ОСШ, обеспечиваемый двухэтапным накопителем при 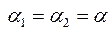, равен:

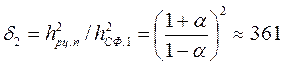. (П.1-15)

2. Построить СФ для радиоимпульса

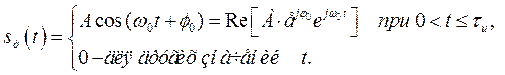(П.1-16)

где φ₀ – начальная фаза колебания радиоимпульса с частотой ω₀;

СПА радиоимпульса для положительных частот ω > 0 можно представить (на основании теоремы о смещении спектра 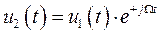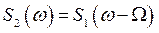) в виде произведения смещенной по частоте на (ω–ω₀) СПА огибающей радиоимпульса (П.1-3) 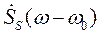(т. е. видеоимпульса (П.1-2)) и фазового множителя :

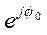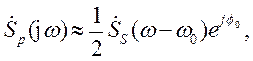(П.1-17)

Следовательно коэффициент передачи СФ (П.1-1) для радиоимпульса (П.1-16) можно выразить через коэффициент передачи СФ (П.1-4) для огибающей радиоимпульса, т.е. видеоимпульса (П.1-2):

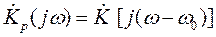. (П.1-18)

Таким образом, для получения выражения коэффициента передачи СФ с радиоимпульсом при АБГШ достаточно в выражении (П.1-4) передаточной характеристики СФ для видеоимпульса подставить вместо ω значения (ω – ω₀) и получим при задержке в СФ t₀ = τ_и :

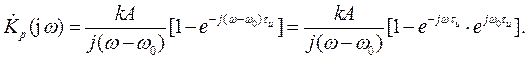(П.1-19)

Множитель 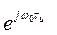можно представить в виде

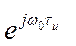
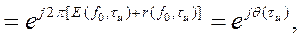
где 2πЕ(f_0,τ_u) – целая по модулю 2π часть набега фазы за время τ_з= τ_и на частоте f₀, которая не изменяет мгновенное значение колебания на выходе СФ;

2πr(f_0,τ_u) = θ(τ_и) – дробная часть полной фазы, влияющая на значение выходного колебания СФ, которую надо компенсировать фазовращателем.

В этом случае коэффициент передачи СФ для радиоимпульса равен:

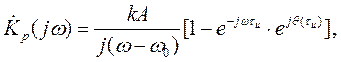(П.1-20)

где 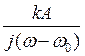– высокочастотное (ВЧ) интегрирующее устройство, реализуемое коэффициентом передачи узкополосного высокоизбирательного резонансного усилителя (ВИРУ).

Схема реализации СФ радиоимпульса представлена на рис.П.4, где сдвиг фазы на θ(τ_и) обеспечивает когерентность колебаний на входах вычитателя.

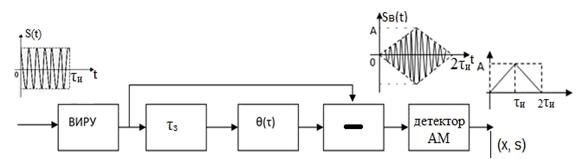
Рис. П.1-5. Функциональная схема СФ для прямоугольного радиоимпульса.

Эпюры формирования напряжения на выходе СФ S_в(t) и АМ детектора.

Следует отметить, что если на входе приемника действует смесь сигнала s(t) с известными параметрами и АБГШ n(t)

x(t) = s(t)+ n(t),

то в задачах обнаружения или различения сигналов оптимальный

приемник вычисляет коррелятором или СФ (Рис.П.1-6) скалярное произведение (корреляционный интеграл) [4, 29]:

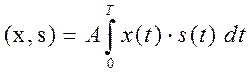, (П.1-21)

значение которого в момент Т сравнивается (например, в задачах обнаружения) с порогом.

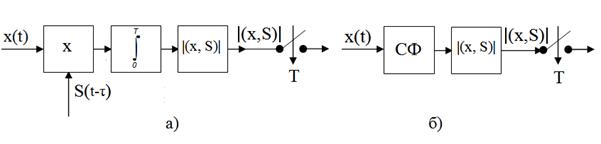
Рис. П.1-6. Схемы: а) коррелятора (активного фильтра); б) пассивного СФ.

Коррелятор реализует линейные операции: вычисление произведения x(t) s(t) и интегрирование. При этом режим его работы зависит от s(t-τ) во времени, т. е. он является линейным параметрическим устройством (активным фильтром).

СФ является пассивным фильтром с зеркальной ИХ g(t) = s(Т – t) (Рис. П.1-1), параметры которого постоянны во времени. При этом выходное напряжение в момент Т согласно интегралу Дюамеля совпадает с точностью до постоянного коэффициента с выходным скалярным произведением коррелятора.

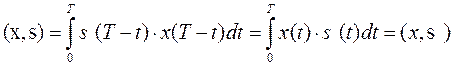. (П.1-22)

Следовательно, СФ инвариантен относительно задержки сигнала и его начальной фазы, а коррелятор не инвариантен.

Например, при случайной начальной фазе s(t) на выходе СФ необходим детектор для выделения огибающей, а в корреляторе (при некогерентном приеме) необходим второй (квадратурный) канал и схема вычисления огибающей.

Вместе с тем в задачах различения сигналов s_i(t) и s_j(t) при этих же условиях и приеме по огибающей радиосигнала на выходе СФ:

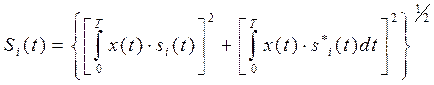(П.1-23)

необходимо дополнительное ограничение на сигналы:→ ортогональность их в усиленном смысле, чтобы отклик огибающей на выходе СФ канала iна сигнал s_j(t) был равен нулю.

3. Построить СФ для КП Баркера длиной 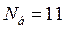импульсов рис. П.1-7а, где согласно таблице 2.1 [5] «±» соответствует сдвигу фазы огибающей модулированного радиосигнала ФМ-2 на «0, π» и соответственно значению этой действительной огибающей «+1, -1» (бинарный сигнал БВН):

τи

Рис.П.1-7.а. Изображение КП Баркера S(t) огибающей ФМ-2 сигнала.

Импульсная характеристика СФ g(t) (Рис.П.1-1) для сигнала Рис.П.1-7.а при t₀ = 0 является зеркальной к сигналу изображения:

τи

Рис.П.1-7.б. Импульсная характеристика СФ g(t) для КП Баркера при t₀ = 0.

Устройство, реализующее СФ, представлено на рис.П.1-8.

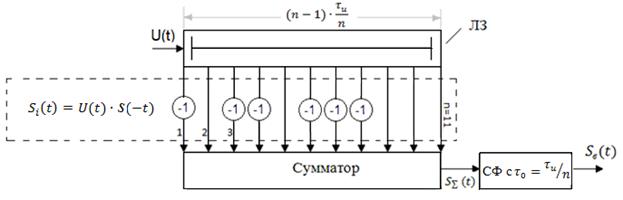
Рис П.1-8. Устройство, реализующее СФ для сигнала КП Баркера N_б = 11.

Формирование выходной сигнальной функции СФ представлено

на рис. П.1-9, где импульсы «пачки» рис. П.1-7а поступают на вход ЛЗ (Рис.П.1-8) в последовательности слева направо.

Sв(t)

а)

SΣ(t)

в)

б)

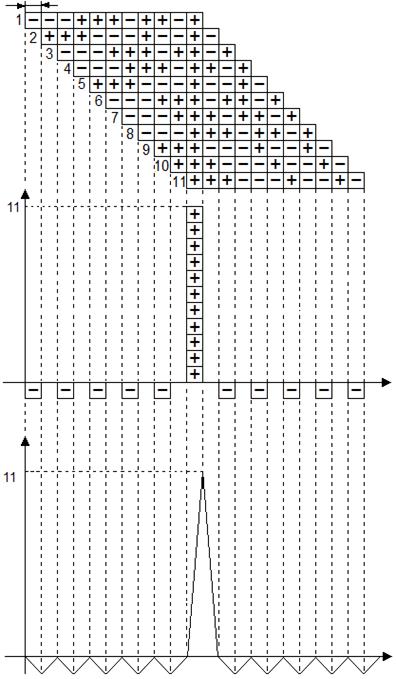
Рис.П.1-9: а) формирование радиоимпульсов S_i(t) на входах 1,2,..11 сумматора ∑ ;

б) результат суммирования на выходе сумматора S_Σ(t) ;

в) сигнальная функция S_в(t) на выходе СФ.

На рис.П.1-9: а) изображены сдвинутые во времени (с учетом инверсных каскадов) радиоимпульсы 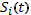на входах 1,2,…11 сумматора (Рис.П.1-6). Результаты когерентного суммирования S_Σ(t)представлены на рис. П.1-9б. Результирующий сигнал S_в(t) на выходе СФ с импульсом длительностью 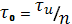приведен на рис. П.1-9в).

Уместно отметить, что если на выходе СФ шум превышает уровень боковых пиков АКФ сигнала Баркера, то можно реализовать на выходе такого СФ накопление сигнала на РЦ, как и выше для видеоимпульсов, по нескольким периодически излучаемым сигналам Баркера. При этом период этих сигналов должен превышать интервал корреляции шумов на выходе СФ, т. е. длительность сигнала Баркера. Однако при этом предельное значение ОСШ будет определяться отношением уровня главного максимума АКФ сигнала Баркера к ее максимальному боковому пику.