Интегрирование простейших иррациональных функций
Интегрирование элементарных дробей
| Тип инт. | Вид интеграла | Знак D | № сп. | Способ решения | пример |
| I | 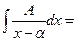 | = 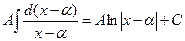 | 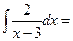 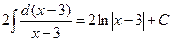 | ||
| II | 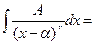 | = 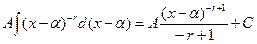 | 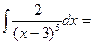 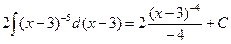 | ||
| III | 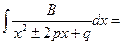 | D>0 | №1 | Найдем корни многочлена: 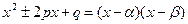 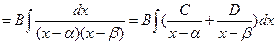 | 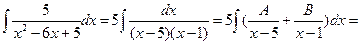 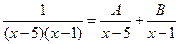 1=A(x-1)+B(x-5) 1=A(x-1)+B(x-5) 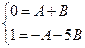 A= A= 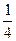 , B=- , B=- 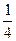 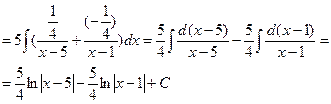 |
| D>0, D<0 | №2 | Выделим полный квадрат: 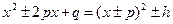 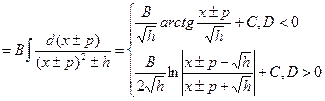 | 1) 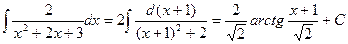 2) 2) 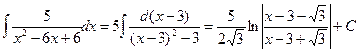 | ||
| D=0 | Cмотри решение интеграла типа II | 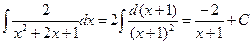 | |||
| I˅ | 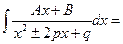 | D>0 | №1 №2 | См. III (разлагаем подынтегральную функцию на сумму элементарных дробей) -редко | 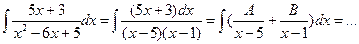 |
| D>0, D<0 | №3 | Выделяем в числителе производную квадратного трехчлена: (числа E, F находим подбором)  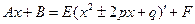 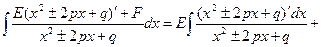 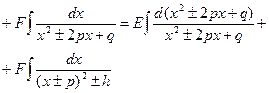 | 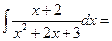 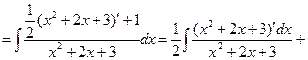 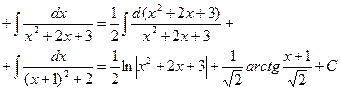 | ||
| D=0 | Разбиваем на 2 интеграла | ||||
| ˅ | 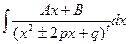 | Аналогичные решения | |||
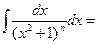 | Формула приведения: 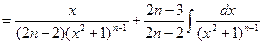 |
Интегрирование тригонометрических функций
I 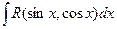 (рациональная функция) (рациональная функция) | |||
Общий случай, например, 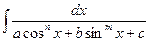 | Сводится к интегралам от рациональных функций с помощью универсальной подстановки: 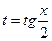 , тогда , тогда  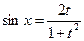 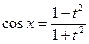 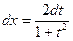 | 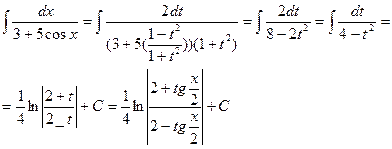 | |
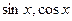 под знаком интеграла содержатся только в четных степенях под знаком интеграла содержатся только в четных степенях | Сводим к 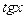 или или 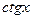 и делаем подстановку: и делаем подстановку: 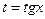 или или 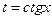 Используются формулы: Используются формулы: 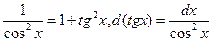 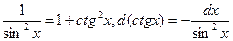 | 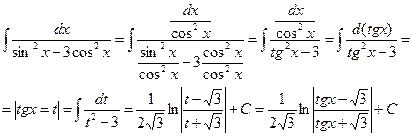 | |
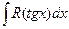 | Делаем подстановку 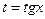 , тогда , тогда 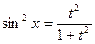 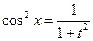 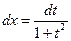 | 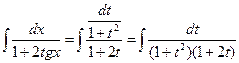 - интеграл от рациональной дроби - интеграл от рациональной дроби | |
II 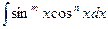 | |||
| Если хотя бы одно из m или n нечетное, положительное целое | Отделяем от нечетной степени один сомножитель, подводим его производную под знак дифференциала, оставшуюся четную степень выражаем с помощью формулы: 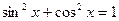 | 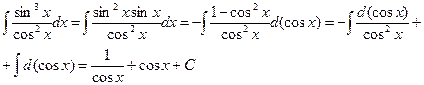 | |
| Если m и n – оба четные, неотрицательные (одно из них м.б. равным нулю) | Понижаем степени с помощью формул: 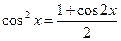 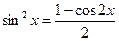 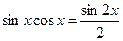 | 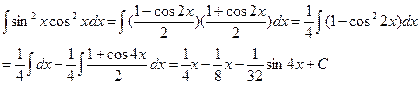 | |
| Если сумма (m + n) – целая, четная, отрицательная | Сводим к 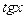 или или 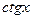 и делаем подстановку: и делаем подстановку: 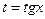 или или 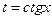 Используются формулы п. I.2 Используются формулы п. I.2 | 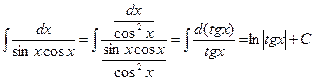 | |
| Если один из m или n равен нулю, а второй – нечетное, отрицательное число | 1)Делаем подстановку: 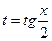 , при этом используются формулы п. I.1. 2) Либо с помощью замены сводим к интегралу от рациональной дроби. 3) Либо используются формулы приведения. , при этом используются формулы п. I.1. 2) Либо с помощью замены сводим к интегралу от рациональной дроби. 3) Либо используются формулы приведения. | 1) 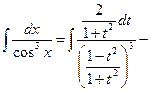 интеграл от рациональной дроби 2) интеграл от рациональной дроби 2) 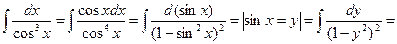 интегралу от рациональной дроби интегралу от рациональной дроби | |
| Если один из m или n равен нулю, а второй – четное, отрицательное число | Делаем подстановку: 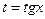 или или 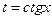 , при этом используются формулы п. I.2. Либо используются формулы приведения , при этом используются формулы п. I.2. Либо используются формулы приведения | 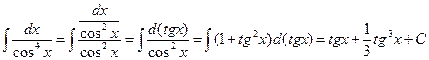 | |
III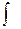 (произведение синусов и косинусов различных аргументов) dx (произведение синусов и косинусов различных аргументов) dx | |||
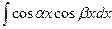 | Используем формулу:   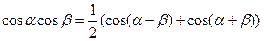 | ||
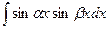 | 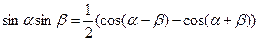 | ||
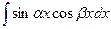 | 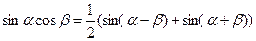 | 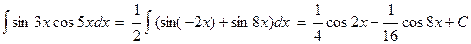 |
Интегрирование простейших иррациональных функций
| № | Вид интеграла | Способ вычисления | Пример |
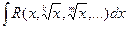 интеграл от рациональной функции интеграл от рациональной функции | Делаем подстановку: 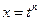 , где n – наименьшее кратное всех показателей k, m, … , где n – наименьшее кратное всех показателей k, m, … | 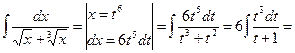 (интеграл от неправильной рациональной дроби, делим уголком)= = (интеграл от неправильной рациональной дроби, делим уголком)= =  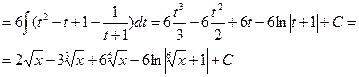 | |
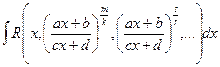 интеграл от рациональной функции, m,k,s,r – целые числа интеграл от рациональной функции, m,k,s,r – целые числа | Делаем замену: 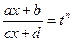 , где n – общий знаменатель дробей , где n – общий знаменатель дробей 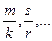 | 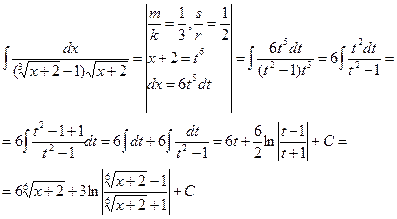 | |
а) 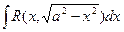 | Делаем подстановку: 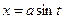 или или 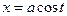 , тогда , тогда 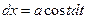 или или 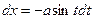 В итоге перейдем к интегралу вида: В итоге перейдем к интегралу вида: 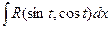 | 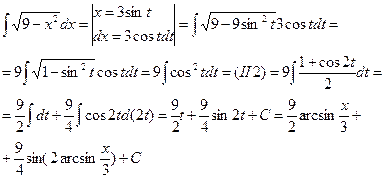 | |
б) 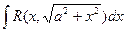 | Делаем подстановку: 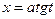 или или 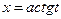 , тогда , тогда 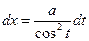 или или 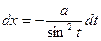 В итоге перейдем к интегралу вида: В итоге перейдем к интегралу вида: 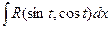 | 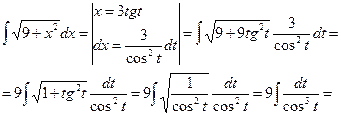 Свели к интегралу II 4 (подстановка Свели к интегралу II 4 (подстановка 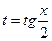 ) ) | |
в) 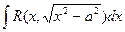 | Делаем подстановку: 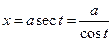 или или 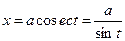 , тогда , тогда 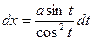 или или 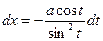 В итоге перейдем к интегралу вида: В итоге перейдем к интегралу вида: 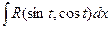 | 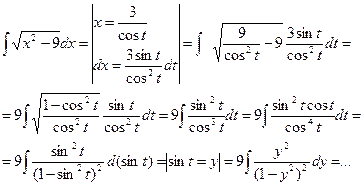 Свели к интегралу от рациональной дроби. Свели к интегралу от рациональной дроби. | |
г) общий случай 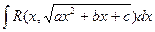 | В квадратном трехчлене выделяем полный квадрат: 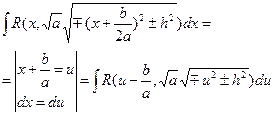 приходим к одному из трех интегралов типа 3a, 3б, 3в приходим к одному из трех интегралов типа 3a, 3б, 3в | 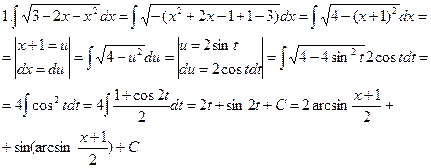 2. 2. 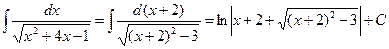 | |
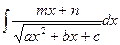 | Предварительно выделяем в числителе производную квадратного трехчлена:  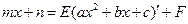 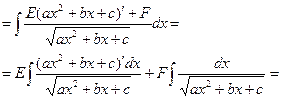 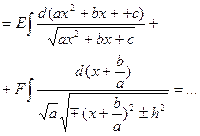 первый и второй – табличные интегралы, первый и второй – табличные интегралы, | 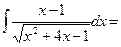 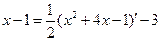 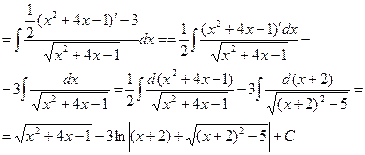 | |
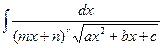 r = 1,2 r = 1,2 | Делаем замену: 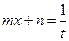 Тогда Тогда 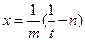 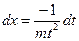 В итоге перейдем к интегралу типа 3 (a, б, в, г) или 4. В итоге перейдем к интегралу типа 3 (a, б, в, г) или 4. | 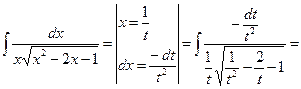 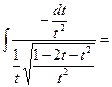 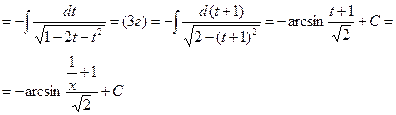 | |
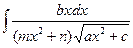 | Делаем замену: 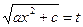 Тогда Тогда 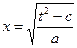 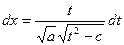 |
