Понятие «Золотого сечения»
В математике пропорцией называют равенство двух отношений a:b=c:d. Отрезок АВ можно разделить на две части следующими способами:
1. На две равные части
2. На две неравные части, но они не образуют пропорцию.
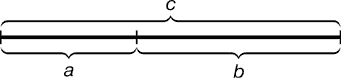
3. Таким образом, что меньшая часть так относится к большей, как
большая ко всей величине. a:b=b:c
Это деление отрезка и есть «Золотое сечение».
«Золотое сечение» в живой природе
С давних пор так повелось: все самое лучшее, ценное и желанное люди называли золотым: чьи-то умелые руки, доброе сердце, отзывчивый характер, незабываемые радостные деньки, покрытые ковром спелой ржи поля. А в трудах Пифагора, Платона, Аристотеля, Евклида нередко упоминается о загадочном «Золотом сечении». Именно оно управляет всей нашей жизнью. Все объекты в природе подчиняются золотой пропорции. Значит именно она и позволяет нам восторгаться природой, значит, золотая пропорция несет в себе гармонию. Спиралевидную форму золотой пропорции можно увидеть в расположении семян подсолнечника, в шишках сосны, в ананасах, кактусах, строении лепестков роз и даже в расположении листьев на ветке, энергия закручивается по спирали. В математике нет более иной формы, которая обладала бы такими же уникальными свойствами как спираль. Спираль - основа всего.
Изучая конструкции раковин, ученые обратили внимание на целесообразность форм и поверхностей раковин: внутренняя поверхность

гладкая, наружная - рифленая. Форма раковин поражает своим совершенством и экономичностью средств, затраченных на ее создание. Идея спирали в раковинах выражена не приближенно, а в совершенной геометрической форме, в удивительно красивой, "отточенной" конструкции.
У большинства улиток, которые обладают раковинами, раковина растет в форме логарифмической спирали, которая точно соответствуют "золотой пропорции".
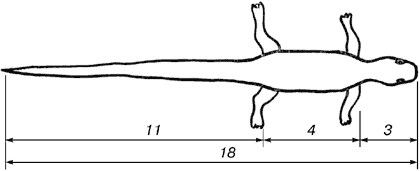
В ящерице с первого взгляда улавливаются приятные для нашего глаза пропорции – длина ее хвоста так относится к длине остального тела, как 62 к 38.
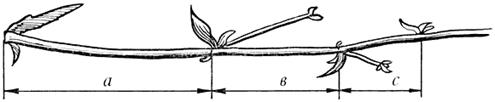
Цикорий. Приглядимся к нему внимательно. От основного стебля образовался отросток. Тут же расположился первый листок. Отросток делает
сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок еще меньшего размера и снова выброс. Если первый выброс принять за 100 единиц, то второй равен 62 единицам, третий – 38, четвертый – 24 и т.д. Длина лепестков тоже подчинена золотой пропорции.
Спиралевидную форму можно увидеть и в расположении семян подсолнечника, и в шишках сосны, в ананасах, кактусах, строении лепестко роз и т.д.
Молекула ДНК состоит из двух вертикально переплетенных между собой спиралей. Длина каждой из этих спиралей составляет 34 ангстрема, ширина 21 ангстрема. (1 ангстрем - одна стомиллионная доля сантиметра).
Так вот 21 и 34 - это цифры, следующие друг за другом в последовательности чисел Фибоначчи, то есть соотношение длины и ширины логарифмической спирали молекулы ДНК несет в себе формулу золотого сечения 1:1,618. Очень совершенна форма стрекозы, которая создана по законам золотой пропорции: отношение длин хвоста и корпуса равно отношению общей длины к длине хвоста.
Многие насекомые (например, бабочки, стрекозы) в горизонтальном разрезе имеют простые асимметричные формы, основанные на золотом сечении.
Заключение
Золотое сечение имеет большое применение в нашей жизни.
Благодаря золотому сечению был открыт пояс астероидов между Марсом и Юпитером – по пропорции там должна находиться ещё одна планета.
На летательных аппаратах с электромагнитными источниками энергии создаются прямоугольные ячейки с пропорцией золотого сечения.
1.Золотое сечение является отображением окружающего мира;
2.Человеческое представление о красивом формировалось под влиянием порядка и гармонии;
3.Закономерности «Золотого сечения» заложены в подсознании человека, они использовались и используются архитекторами, скульпторами, живописцами в своих работах.
Принцип золотого сечения – высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе. Эта пропорция используется практически во всех областях знаний.
Список используемой литературы
1.Азевич А.И. Двадцать уроков гармонии: гуманитарно-математический курс. – М.: Школа-пресс, 1998.
2. Васюткинский Н.Н. Золотая пропорция. – М., 1990.
3. Волошинов А.В. Математика и искусство. – М., 1992.
4.Ковалев Ф.В. Золотое сечение в живописи. К.: Выща школа, 1989.
5.Дюрер А. Дневники, письма, трактаты – Л., М., 1957.
6.Цеков-Карандаш Ц. О втором золотом сечении. – София, 1983.
7.Стахов А. Коды золотой пропорции.8.Интернет ресурсы.
