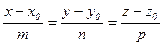Уравнение прямой линии, проходящей через две точки

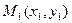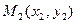Пусть даны точки и . Написать уравнение прямой, проходящей через эти точки.

y

M₂(x₂,y₂)

M(x,y)

M₁(x₁,y₁)

x

l

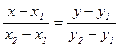
Уравнение прямой линии в отрезках.

Пусть даны точки M₁(a,0) и M₂(0,b) .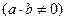

Тогда уравнение прямой линии, проходящей через точки M₁(a,0) и M₂(0,b) имеет вид:

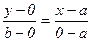или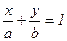

Расстояние от точки до прямой.

Пусть задана прямая l: Ax + By +C = 0 и точка M₀(x₀,y₀). Требуется найти расстояние от точки M₀ до прямой l.

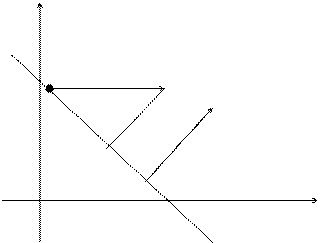Y

M₀ M₁

d

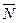
0 x

l

Расстояние d от точки M₀ до прямой l равно модулю проекции вектора 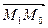, где M₁(x₁,y₁) – произвольная точка прямой l, на направление вектора нормали .

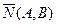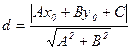
4. Уравнение плоскости в пространстве.

Нормальное уравнение плоскости в пространстве.

Любой вектор 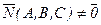, перпендикулярный данной плоскости называется вектором нормали данной плоскости.

Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору.

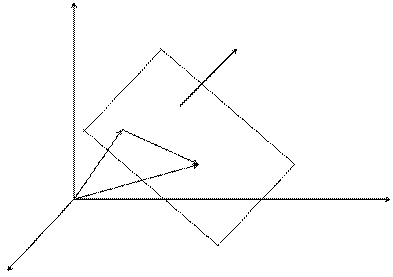
Пусть в прямоугольной системе координат в R³ задана плоскость L, точка M₀(x₀, y₀, z₀) и вектор 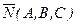перпендикулярен плоскости L. Требуется написать уравнение плоскости L.

z

M₀

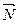
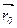
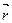M

0 y

L

x

Уравнение (2) – уравнение плоскости, проходящей через точку M₀(x₀,y₀,z₀) перпендикулярно вектору .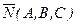

Уравнение плоскости, проходящей через три данные точки.

Пусть в прямоугольной системе координат в R³ заданы три точки 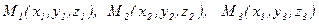, не лежащие на одной прямой. Написать уравнение плоскости L, проходящей через точки M_1, M₂, M₃.

Выберем на плоскости L произвольную точку M(x,y,z). Тогда векторы 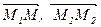и 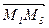лежат в одной плоскости L, а значит они компланарны.

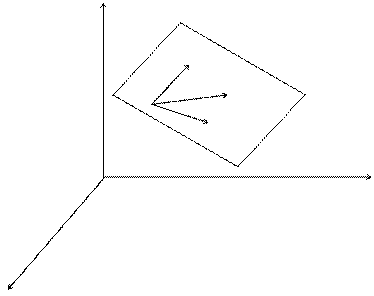
z

M₂

M₁ M L

M₃

0 y

x

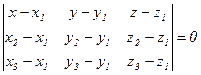
Уравнение плоскости в отрезках

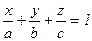
5. Прямая линия в пространстве

Общее уравнение прямой линии в пространстве.

Каждая линия в пространстве есть пересечение двух поверхностей и определяется заданием двух уравнений вида:

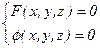
Прямая линия в пространстве есть пересечение двух плоскостей и определяется системой двух уравнений первой степени вида:

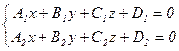(1)

Уравнения прямой линии в проекциях.

Пусть прямая l задана общим уравнением:

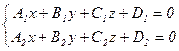
любая точка прямой лежит и на плоскости

Канонические уравнения прямой.

Вектор 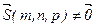, лежащий на прямой 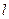или параллельный ей называется направляющим вектором данной прямой l.

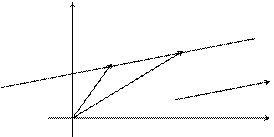
Пусть в пространстве 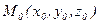и вектор 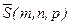, отличный от нулевого. Требуется написать уравнение прямой l в пространстве, проходящей через данную точку M₀, параллельно заданному вектору .

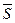y

M

M₀

l

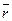
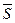
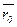
0 x

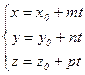- параметрическими уравнениями прямой в пространстве.

Уравнение прямой в пространстве, проходящей через две заданные точки.

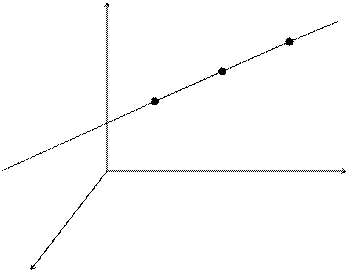
Пусть в пространстве заданы две точки M₁(x₁,y₁,z₁) и M₂(x₂,y₂,z₂). Требуется написать уравнение прямой l в пространстве, проходящей через точки M₁ и M₂.

z

M₂

M

M₁

l

0 y

x

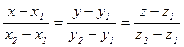- прямой линии в пространстве, проходящей через две заданные точки.

канонический вид: