Частичный разряд емкостных накопителей
При анализе процесса разряда емкостного накопителя пренебрегаем током заряда в схеме (см. рис. 4.1) на отрезке времени 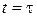 . Исходя из схемы, получим:
. Исходя из схемы, получим:
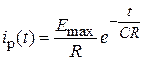 ;
; 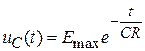 . (4.2)
. (4.2)
Время отсчитывается от момента замыкания коммутатора. Так как этот момент соответствует моменту окончания процесса заряда, то начальное напряжение на емкости С равно Еmax. Через R обозначено полное сопротивление цепи разряда, равное сумме сопротивления нагрузки и сопротивления коммутатора в замкнутом состоянии. При частичном разряде емкостного накопителя постоянная времени цепи разряда существенно больше длительности импульса тока нагрузки, т. е. tраз = RC > t. В этом случае напряжение накопителя уменьшается в процессе разряда на величину, определяемую временем включенного состояния коммутатора.
На рис. 4.7 приведены форма импульса напряжения на нагрузке (рис. 4.7, а) и характер изменения напряжения на накопительной емкости (рис. 4.7, б).
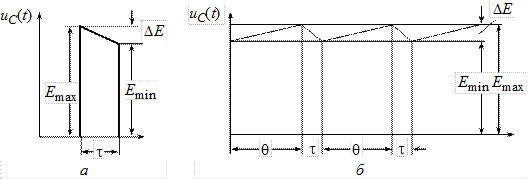
Рис. 4.7
При проектировании генераторов с частичным разрядом емкостного накопителя основной задачей является определение минимально допустимой величины накопителя С, при которой величина спада вершины импульса DЕ не превышает заданных значений. При этом задаются значением сопротивления нагрузки R, максимальной длительностью импульса t, амплитудой тока нагрузки Imaxи допустимой величиной DЕ = Еmax – Еmin. Величина Еmaxопределяется значением тока и равна Еmax = ImaxR. Как следует из (4.2), процесс разряда емкостного накопителя происходит по экспоненте, и анализ этого процесса традиционно производится во временнóй области. При определении величины емкостного накопителя обычно делались допущения, физический смысл которых сводится к тому, что на начальных участках экспоненциальный закон изменения напряжения 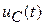 может быть заменен линейным. Результатом этого анализа является расчетная формула, имеющая вид
может быть заменен линейным. Результатом этого анализа является расчетная формула, имеющая вид
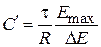 , (4.3)
, (4.3)
которая дает несколько завышенный результат [2], [7].
Оценим требуемую минимальную величину емкостного накопителя несколько иначе, исходя из закона сохранения заряда. Величины зарядов – потребленного от накопителя 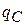 и протекшего через нагрузку
и протекшего через нагрузку 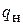 – равны друг другу. Тогда
– равны друг другу. Тогда 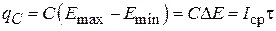 . Так же считая, что на начальном участке экспонента может быть заменена прямой линией, примем среднее значение тока нагрузки равным
. Так же считая, что на начальном участке экспонента может быть заменена прямой линией, примем среднее значение тока нагрузки равным
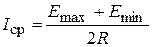 .
.
Отсюда следует, что
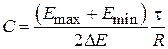 . (4.4)
. (4.4)
Тщательный анализ показывает, что зависимость (4.4) дает практически точный результат даже при значениях 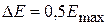 . Превышение величины емкостного накопителя
. Превышение величины емкостного накопителя 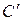 , рассчитанного по (4.3), над величиной емкостного накопителя С, рассчитанного по (4.4), и равное
, рассчитанного по (4.3), над величиной емкостного накопителя С, рассчитанного по (4.4), и равное 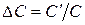 , уже при значениях
, уже при значениях 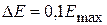 составляет 5,3 % и увеличивается с ростом величины DЕ. При значениях
составляет 5,3 % и увеличивается с ростом величины DЕ. При значениях 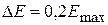 значение DС = 11 %, при
значение DС = 11 %, при 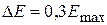 DС = 17 % и при
DС = 17 % и при 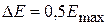 DС = 33 %. С учетом высокой стоимости высоковольтных импульсных конденсаторов и ограниченности номенклатуры их номиналов приведенный уточненный расчет является более предпочтительным.
DС = 33 %. С учетом высокой стоимости высоковольтных импульсных конденсаторов и ограниченности номенклатуры их номиналов приведенный уточненный расчет является более предпочтительным.
4.3. Частичный разряд эквивалентных
формирующих двухполюсников
В случае использования ФД в режиме частичного разряда возникает вопрос о выборе вида ФД с учетом КПД процесса разряда, поскольку различные структуры ФД могут проявить себя по-разному. Ответом на этот вопрос является следующая теорема [13].
Теорема. КПД процесса частичного разряда эквивалентных ФД инвариантен относительно их структуры.
Прежде чем перейти к доказательству теоремы, отметим, что реальные реактивные элементы ФД имеют конечную добротность и, следовательно, конечную длительность переходного процесса, возникающего в ФД с момента отключения тока нагрузки. При этом потерями в ФД за время формирования импульса (t £ tmax) в нагрузке можно пренебречь, так как добротность реактивных элементов достаточно велика.
Для доказательства теоремы рассмотрим КПД процесса генерирования одиночного импульса:
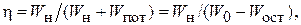 (4.5)
(4.5)
где Wн– энергия, выделившаяся в нагрузке к моменту времени отключения силового ключа; Wпот– энергия, теряемая в элементах ФД после отключения ключа; W0– начальная энергия ФД; Wост– энергия, оставшаяся в емкостях ФД по окончании переходного процесса.
По определению эквивалентных цепей токи i(t) и напряжения u(t) на их внешних зажимах одинаковы, следовательно, значение начальной энергии
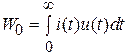 (4.6)
(4.6)
и значение энергии, выделенной в нагрузке за время импульса,
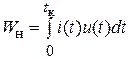 (4.7)
(4.7)
не зависят от структуры ФД.
Покажем равенство значений энергий, оставшихся в эквивалентном ФД после окончания переходного процесса. Начальные заряды эквивалентных ФД равны между собой:
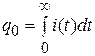 . (4.8)
. (4.8)
Отсюда, в частности, следует равенство статических емкостей эквивалентных ФД, так как Cст = q0/E, поскольку равны начальные значения напряжения заряда E, что является следствием равенства переходных проводимостей ФД. Зависимость (4.8) означает, что за время t ®¥ через нагрузку протечет заряд, который полностью скомпенсирует равные по значению отрицательные и положительные заряды, находившиеся на обкладках Сств начальный момент времени. За время tкчерез нагрузку протечет заряд
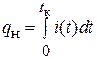 (4.9)
(4.9)
и в ФД останутся нескомпенсированными заряды
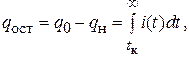
равные для эквивалентных ФД на основании (4.8) и (4.9).
С момента времени tкв отсоединенных от нагрузки двухполюсниках начинается переходный процесс установления остаточного напряжения Uост, который в любом случае заканчивается при t ®¥, причем из закона сохранения заряда следует, что
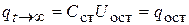 . (4.10)
. (4.10)
Из зависимости (4.10) с учетом равенства статических емкостей эквивалентных ФД вытекает и равенство напряжений Uост. Следовательно, равны и значения оставшейся в эквивалентных ФД энергии:
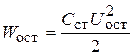 . (4.11)
. (4.11)
Поскольку КПД (4.5) определяется только значениями из (4.6), (4.7) и (4.11), которые инвариантны по отношению к структуре ФД, теорема доказана.
Отметим, что при доказательстве теоремы не использовалось условие работы на активную линейную нагрузку, в силу чего теорема справедлива и для нелинейных нагрузок произвольного вида.
Основным следствием из данной теоремы является то, что КПД процесса частичного разряда не может быть критерием выбора структуры ФД для ГИТРД.
4.4. Энергетика процессов частичного разряда
однородной искусственной линии
Доказанная в 4.3 теорема позволяет произвести количественную оценку энергетики процессов частичного разряда эквивалентных ФД на примере ОИЛ, которая при бесконечном числе звеньев является ЛРП. Рассмотрим два режима работы – на согласованную и на рассогласованную нагрузки.
При работе на согласованную нагрузку за время tкв нагрузке выделится энергия Wн = W0t*, где t* = tк/tmax; 0 £ tк £ tmax. Начальная энергия ЛРП W0 = 0,5q0U0.
Оставшаяся по завершении переходного процесса в линии энергия
Wост = 0,5qостUост. (4.12)
Значение остаточного заряда
qост = q0(1 – t*).
Отсюда Uост = qост/C0 = q0(1 – t*)/C0 = U0(1 – t*). Тогда из (4.12) получим:
Wост = 0,5q0U0(1 – t*)2.
Энергия потерь, рассеянная в линии в результате колебательного процесса при t > tк,
Wпот = W0– Wн– Wост = 0,5q0U0(1 – t*)t.*
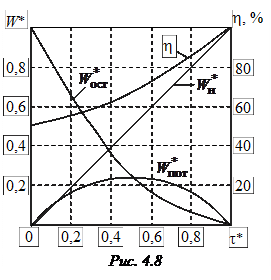 При этом КПД частичного разряда согласованной с нагрузкой линии h = 1/(2 – t*). На рис. 4.8 приведены энергетические характеристики, где в относительных величинах представлены зависимости W* = W/W0и КПД от относительной длительности импульса t*. Анализ этих зависимостей позволяет сделать вывод, что частичный разряд согласованной с нагрузкой линии сопровождается значительными потерями энергии, которые максимальны при t* = 0,5, когда энергия, запасенная в распределенной индуктивности линии, максимальна. КПД монотонно убывает от 100 % (t* = 1) до 50 % (t*® 0), и практический интерес представляет только интервал регулирования длительности от 0,9t*до t*, когда h ³ 90 %.
При этом КПД частичного разряда согласованной с нагрузкой линии h = 1/(2 – t*). На рис. 4.8 приведены энергетические характеристики, где в относительных величинах представлены зависимости W* = W/W0и КПД от относительной длительности импульса t*. Анализ этих зависимостей позволяет сделать вывод, что частичный разряд согласованной с нагрузкой линии сопровождается значительными потерями энергии, которые максимальны при t* = 0,5, когда энергия, запасенная в распределенной индуктивности линии, максимальна. КПД монотонно убывает от 100 % (t* = 1) до 50 % (t*® 0), и практический интерес представляет только интервал регулирования длительности от 0,9t*до t*, когда h ³ 90 %.
Покажем, что рассогласование линии с нагрузкой в сторону уменьшения волнового сопротивления линии 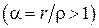 позволяет повысить КПД генератора практически до любого заданного уровня.
позволяет повысить КПД генератора практически до любого заданного уровня.
Действительно, для формирования в одной и той же нагрузке R импульса тока с амплитудой I и максимальной длительностью tmaxпараметры рассогласованной ЛРП должны удовлетворять следующим условиям:
С2 = tmax/2r = tmaxa/2R = C1a;
L2 = L1/a;
U02 = I(R + r) = U0(a + 1)/2a,
где C1, L1, U0– емкость, индуктивность и напряжение заряда согласованной линии.
В нагрузке выделится энергия
Wн = I2Rtmaxt*.
Начальное значение энергии рассогласованной линии
W02 = C2U202/2 = W0(a + 1)2/4a = I2Rtmax(a + 1)2/4a.
Остаточная энергия в рассогласованной линии Wост2определяется уровнем остаточного напряжения Uост2, которое найдем, используя закон сохранения заряда:
Uост2 = qост2/C2 = (q02– qн2)/C2 = IR(a + 1 – 2t*)/a,
где q02 = C2U02 = C2IR(a + 1)/a, qн2 = Itmaxt* = 2IRC2t*/a.
Остаточная энергия
Wост2 = С2U2ост2/2 = I2Rtmax(a + 1 – 2t*)2/4a.
Отсюда КПД генератора на основе ЛРП, работающей в рассогласованном режиме,
h2 = Wн2/(W02– Wост2) = a/(a + 1 – t*).
На рис. 4.9 приведены зависимости h = f(t*) для различных значений коэффициента согласования a, а на рис. 4.10 – зависимости КПД, напряжения заряда линии и энергии от a.
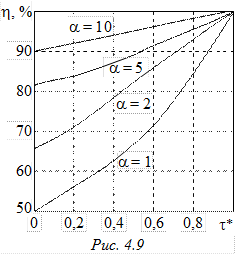
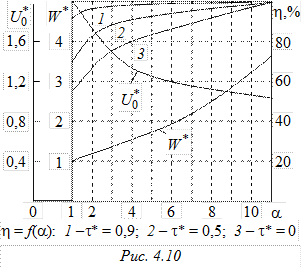
 Анализ этих зависимостей позволяет сделать основной вывод о том, что рассогласование дает возможность существенно повысить КПД процесса частичного разряда и снизить значение зарядного напряжения линии при незначительном увеличении начальной энергии линии. Все изложенное справедливо и для ОИЛ с конечным числом элементов. При этом характер всех зависимостей сохраняется, а абсолютное значение отклонений всех величин не превышает 10 % уже при n = 4, уменьшаясь с ростом числа ячеек. Тем не менее несмотря на приемлемую энергетику частичного разряда рассогласованной линии практическая реализация таких генераторов существенно ограничивается из-за длительного переходного процесса в линии после отключения тока нагрузки, определяемого высокой добротностью реактивных элементов. Это резко снижает предельные значения рабочих частот данных генераторов, что в большинстве случаев неприемлемо. Выходом из указанной ситуации является техническое решение, описываемое далее.
Анализ этих зависимостей позволяет сделать основной вывод о том, что рассогласование дает возможность существенно повысить КПД процесса частичного разряда и снизить значение зарядного напряжения линии при незначительном увеличении начальной энергии линии. Все изложенное справедливо и для ОИЛ с конечным числом элементов. При этом характер всех зависимостей сохраняется, а абсолютное значение отклонений всех величин не превышает 10 % уже при n = 4, уменьшаясь с ростом числа ячеек. Тем не менее несмотря на приемлемую энергетику частичного разряда рассогласованной линии практическая реализация таких генераторов существенно ограничивается из-за длительного переходного процесса в линии после отключения тока нагрузки, определяемого высокой добротностью реактивных элементов. Это резко снижает предельные значения рабочих частот данных генераторов, что в большинстве случаев неприемлемо. Выходом из указанной ситуации является техническое решение, описываемое далее.
