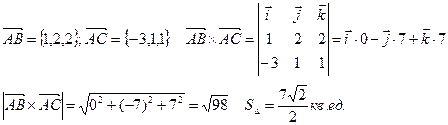Свойства скалярного произведения
1. Скалярное произведение не зависит от порядка сомножителей (переместительное свойство):
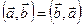 .
.
2. Скалярный множитель можно выносить за знак скалярного произведения:
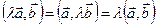 .
.
3. Скалярное произведение двух векторов подчиняется распределительному закону:
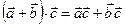 .
.
4. Скалярное произведение двух векторов равно нулю тогда и только тогда, когда векторы  и
и 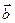 перпендикулярны или один из них равен нулю.
перпендикулярны или один из них равен нулю.
5. 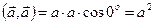 , т.е.
, т.е. 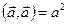 - скалярный квадрат.
- скалярный квадрат.
Таким образом 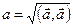
Скалярное произведение в координатной форме.
Пусть 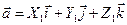 и
и 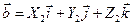 .
.
Тогда
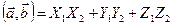 (2)
(2)
Скалярное произведение двух векторов равно сумме парных произведений одноименных координат.
Пример. 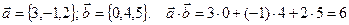 .
.
Модуль вектора. Расстояние между двумя точками.
По свойству (5): 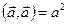 , но
, но 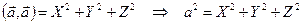 и
и
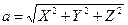 (3)
(3)
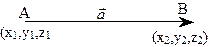 Расстояние между двумя точками А и В равно
Расстояние между двумя точками А и В равно 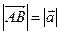
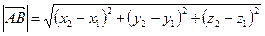
Угол между двумя векторами. Условие перпендикулярности двух векторов.
Из определения скалярного произведения следует: 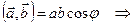
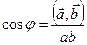 . По формулам (2) и (3) имеем:
. По формулам (2) и (3) имеем:
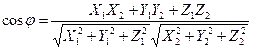
Условие перпендикулярности двух векторов 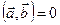 в координатной форме имеет вид:
в координатной форме имеет вид:
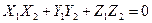
Векторное произведение двух векторов.
Скалярное произведение двух векторов 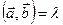 - число, а
- число, а
Векторное произведение 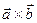 или
или 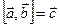 - вектор.
- вектор.
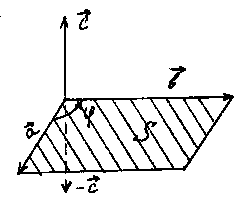
Векторным произведением двух векторов  и
и 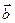 , взятых в определенном порядке, называется третий вектор
, взятых в определенном порядке, называется третий вектор 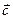 , длина которого численно равна площади параллелограмма, построенного на векторах
, длина которого численно равна площади параллелограмма, построенного на векторах  и
и 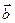 ; направлен вектор
; направлен вектор 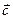 перпендикулярно плоскости, в которой лежат векторы
перпендикулярно плоскости, в которой лежат векторы  и
и 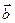 , причем в ту сторону, откуда кратчайший поворот от
, причем в ту сторону, откуда кратчайший поворот от  к
к 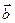 виден против часовой стрелки.
виден против часовой стрелки.
Обозначается: 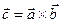 или
или 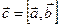 .
.
 Модуль векторного произведения:
Модуль векторного произведения:
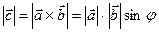
Механический смысл векторного произведения.
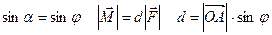 .Поэтому
.Поэтому 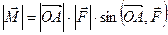 ,
, 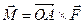 .
.
Момент силы, приложенной к точке А есть векторное произведение радиус-вектора 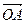 точки приложения силы и силы
точки приложения силы и силы 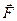 . Направлен вектор
. Направлен вектор 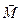 вдоль оси вращения.
вдоль оси вращения.
Свойства векторного произведения.
1. Векторное произведение равно нулю тогда и только тогда, когда векторы  и
и 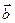 коллинеарны.
коллинеарны.
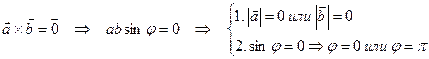
2. При изменении порядка сомножителей векторное произведение меняет знак на противоположный:
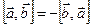 (видно из чертежа)
(видно из чертежа)
3. Скалярный множитель можно выносить за знак векторного произведения.
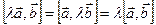
a) площади параллелограммов слева и справа равны.
b) Направление векторов 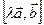 и
и 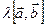 совпадают.
совпадают.
4. Имеет место распределительный закон:
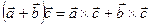 (без доказательства)
(без доказательства)
5. 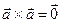 , т.к. ц=0.
, т.к. ц=0.
Векторное произведение в координатной форме.
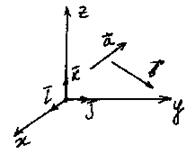 Пусть
Пусть 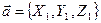 и
и 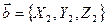
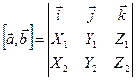
Этот определитель – символический, т.к. первая строка состоит не из чисел, а из векторов.
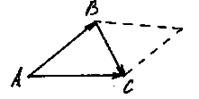 Пример. Даны три точки: А (2, -1, 0); В (3, 1, 2) и С (-1, 0, 1). Найти площадь ДАВС.
Пример. Даны три точки: А (2, -1, 0); В (3, 1, 2) и С (-1, 0, 1). Найти площадь ДАВС.
1. Найти длины 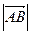 ,
, 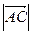 и
и 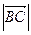 и воспользоваться формулой Герона.
и воспользоваться формулой Герона.
2. 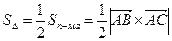 .
.