Каноническое ур-е эллипса, его фокус эксцентриситет и директриса
Фокусы эллипса –2 точки плоскости, сумма расстояний от которых до мн-ва точек, описывающих эллипс суть величина постоянная и большая, нежели расстояние между фокусами.
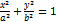 - каноническое ур-е эллипса.
- каноническое ур-е эллипса.
Эксцентриситет эллипса – отношение C к А. С – половина расстояния между фокусами, А – большая полуось эллипса.
Директриса – прямая, лежащая в плоскости конического сечения и обладающая след св-вом: отношение расстояния от любо точки эллипса до его фокуса к расстоянию от этой же точки до директрисы равно его эксцентриситету.
Каноническое ур-е гиперболы. Фокус, эксцентриситет, директриса.
Фокусы гиперболы – две точки плоскости, таких, что модуль разности между точками пространства, описывающими гиперболу и фокусами есть величина постоянная и меньшая, чем расстояние между фокусами.
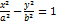 - каноническое уравнение гиперболы.
- каноническое уравнение гиперболы.
Эксцентриситет гиперболы – отношение С к А, С – половина расстояния между фокусами, А – действительная полуось гиперболы.
Директриса - прямая, лежащая в плоскости конического сечения и обладающая след св-вом: отношение расстояния от любо точки гиперболы до его фокуса к расстоянию от этой же точки до директрисы равно ее эксцентриситету.
Каноническое ур-е параболы. Фокус, директриса.
Фокус параболы – точка, описывающая середину расстояния между мн-вом точек, описывающих параболу и директрисой.
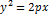 - каноническое ур-е параболы.
- каноническое ур-е параболы.
Директриса - прямая, лежащая в плоскости конического сечения и обладающая след св-вом: отношение расстояния от любо точки параболы до его фокуса к расстоянию от этой же точки до директрисы равно ее эксцентриситету.
Определение ограниченного (сверху,снизу) числового мн-ва.
{x} – ограниченное сверху, если сущ число М, для которого любой эл-т {х} выполняет неравенство
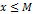 . М называют верхней гранью мн-ва х.
. М называют верхней гранью мн-ва х.
{х}- ограниченное снизу, если сущ m, для которого все эл-ты {x} выполняют неравенство 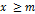 . m – нижняя грань.
. m – нижняя грань.
Определение точной верхней грани числового мн-ва.
M – точная верхняя грань {x}, если М 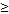 x, и для любого Е>0 эл-т х1, принадлежащий {х} выполняет х1>M-Е.
x, и для любого Е>0 эл-т х1, принадлежащий {х} выполняет х1>M-Е.
Определение точной нижней грани числового мн-ва.
м – точная нижняя грань {x}, если м 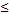 x и для любого Е>0 и х1, принадлежащего {х} выполняется х1<м+Е
x и для любого Е>0 и х1, принадлежащего {х} выполняется х1<м+Е
Теорема о существовании точной верхней(нижней) грани числового мн-ва.
Если непустое мн-во Х ограничено сверху (снизу), то существует единственная точная верхняя (нижняя) грань этого мн-ва.
Определение ограниченной числовой последовательности.
Последовательность {Xn} называет ограниченной, если сущ такое A>0, что для любого n выполняется |Xn| 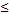 А.
А.
