Предметы должны найти в нем свое положение, образовать художественно-образную и функциональную целостность

Макеты интерьеров изготавливаются в масштабах от 1:10 до 1:50. Бывают и исключения, особенно при макетировании фрагментов интерьера, когда масштаб увеличивается до 1:5. Форма предметов, наполняющих пространство интерьера, моделируется условно. Стены помещения при эскизировании чаще всею не моделируются, поиск ведется на условном пространстве пола. Из пенопласта очень схематично вырезается мебель, станки или другое оборудование, если их формы несложны по структуре. Предметы, более легкие на вид, можно делать из бумаги, выгибать из проволоки. Такие элементы макета, обладающие минимальной прочностью, перемещают по плоскости пола, добиваясь наилучшего их расположения.

Чистовые макеты интерьеров ограничивают двумя, реже тремя стенами, которые могут изготовляться из картона, бумаги и листовых полимерных материалов. В учебных условиях макеты из бумаги вполне удовлетворяют требованиям методики проектирования. Предметы выполняются из бумаги, иногда в сочетании с проволокой и пенопластом. В некоторых случаях для большей информативности пользуются сочетаниями разных материалов. Пол можно оклеить темной бумагой, мебель выделить тоном на фоне выклеенных из серого или коричневого картона стен. Это дает и дополнительный эстетический эффект.

Макет интерьера из листовых полимерных материалов предпочтительнее, чем бумажный, но дороже и сложнее в изготовлении. Сначала выполняются все составные элементы архитектуры и оборудования, затем монтируются стены и пол, на котором размещаются предметы обстановочного комплекса (рис ). Такой макет в чистовом исполнении может быть оставлен в первоначальном материале, даже прозрачном (оргстекло). Но чаще весь макет окрашивается белой эмалью. При крупном масштабе интерьера из различных материалов может быть введена проволока, поролон, пенопласт, текстильная ткань, древесный шпон.

Макетирование территорий

При проектировании планировки территории (жилого квартала, детской площадки, пришкольного участка и д.р.) основная композиционная задача состоит в размещении объемов в открытом пространстве. В некоторых случаях учитывается и воспроизводится в макете рельеф местности. Сначала изготавливается подмакетник и на него наносятся исходные детали (строения, основные дороги, водоемы и др.), не подлежащие изменению.

Предполагаемое оборудование территории макетируется поначалу приблизительно, в «массах», чего вполне достаточно, чтобы вести поиски планировочного решения. Мелкий масштаб планировочных макетов (1:100, 1:200 и 1:500) требует еще большей обобщенности форм предметов, чем при макетировании интерьеров (рис)

Объекты вырезаются из пенопласта, выклеиваются из бумаги, картона. После того как их размещение на площадке найдено, они закрепляются. Иногда плоскость планшета покрывают слоем пластилина толщиной 1 — 2 см. Этот материал удобен как для моделировки рельефа местности, так и закрепления всех деталей, включая простейшие сооружения, кустарник и т.п.

Условность эскизного макета и его мелкий масштаб позволяют пользоваться и другими условными материалами. Для макетирования кустарника годится стружка, спутанная проволока, мягкая бумага, спички, кусочки проволоки и др.

Принцип обобщенности, условности форм сохраняется и в чистовом макете планировки оборудования территории. Сооружения лишаются деталей, у природных форм (деревьев, кустарника, травы) передается только характер их поверхности — зеркальная у воды, шероховатая у газона и т.п. Чтобы макет был не только информативным, но представлял собою композиционную целостность, необходимо все его компоненты подчинить одной мере условности, обобщения, придать всем им единый пластический характер. Этому в некоторой степени способствует правильный выбор материалов или ограничение каким-либо одним материалом, например, пенопластом. Так, из пенопласта можно нарезать пластины, которые будут изображать архитектурные строения, бруски пенопласта с поперечными надрезами изобразят стриженую зелень, тонкие пластины с неровными краями, нанизанные на стержень, — деревья, измельченный пенопласт, приклеенный к плоскости, — газон.

Весь макет может быть выполнен из картона и бумаги. Тогда газон будет обозначен наклеенной на подмакетник шкуркой, вода - черной бумагой, деревья — листочками неправильной формы, нанизанными на стержень, кустарник — жатой бумагой и т.п. Можно пользоваться картоном разного цвета, обозначая, например, коричневым архитектурные постройки и малые формы, а серым — газоны и пр.

Помимо перечисленных, имеется много других средств для передачи в макетах проектных замыслов. В частности, для имитации поверхностей дорог, газонов и т.п. широко используются подкрашенные опилки, корундовый порошок, крупа, которые наносятся на поверхность, покрытую слоем клея. Деревья и другую объемную зелень передают кусочки поролона или резиновой губки, скрепленные между собой булавками. Деревья макетируются и с помощью проволоки толщиной 0,8 — 1 мм, из которой свивают нечто вроде спирали, и металлическим стержнем закрепляют их на подмактнике. Часто пользуются естественной зеленью — ветками, оленьим мхом, морской травой и пр.

Существуют определенные приемы имитации водоемов. Нужной формы пластина оргстекла или целлофана накладывается на фольгу или черную бумагу, а иногда сама окрашивается с нижней стороны. Все такие средства применять следует очень осторожно, чтобы не утратить проектную условность. Макет не должен сообщать ни о чем лишнем.

Макет следует снабдить названием объекта и указателем сторон света. Можно рекомендовать шрифт и знак ориентации делать объемными, найдя для них на плоскости макета место, приемлемое с точки зрения общей композиции.

Работа над художественно-конструкторским проектом завершается графикой и макетом из условного материала только в условиях учебного процесса. В реальном проектировании на их основе разрабатывается разнообразная техническая документация: рабочие чертежи с конструкторской проработкой всех узлов и деталей в натуру, а иногда и в увеличенном масштабе (2:1, 2:5 и т.п.). Если изделие не очень велико, то исполняется и модель в натуральную величину. Делают модели и довольно крупных изделий, предназначенных для серийного производства, например, автомобилей. В этих случаях модель выполняется в материалах, предусматриваемых технической документацией.

15. Перспективное изображение.

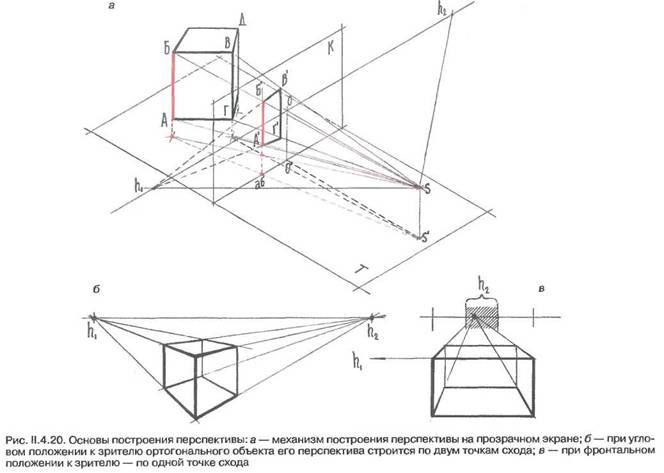
Представим себе, что мы смотрим через стекло на какой-либо предмет. Если обвести на стекле видимый контур предмета восковым карандашом, то получим его изображение в перспективе. Действительно, некоторые из лучей света, отраженных от предмета, сходятся в одной точке — в глазу наблюдателя. Прямолинейное распространение лучей света позволяет рассматривать их как проецирующие прямые, в данном случае пересекающиеся в одной точке. Следовательно, мы имеем дело с центральными проекциями.

Основными элементами перспективного проецирования (рис. IV.25,а) являются центр проецирования — точка С и плоскость проекций К, называемые соответственно точкой зрения и картинной плоскостью, или картиной. В дальнейшем мы будем пользоваться только вертикальной картиной. Кроме того, вводят вспомогательные элементы — горизонтальную предметную плоскость Т, расположенную на любой, необходимой для построений высоте; точка с — прямоугольная проекция точки С на плоскости Т или точка стояния; точка С' — прямоугольная проекция точки С на плоскость К, называемая главной точкой картины. Ее прямоугольную проекцию на плоскость Т — точка с' — называют основанием главной точки. Прямая Т_к — линия пересечения плоскостей К' и Т — основание картины и, наконец, горизонтальная прямая НН, лежащая в плоскости К и проходящая через точку С' — горизонт.

Если смотреть спереди на картинную плоскость (рис. IV.25,в), то увидим горизонт НН с расположенной на ней главной точкой С' и спроецировавшуюся в прямую Т_к плоскость Т. На пересечении этой прямой с перпендикуляром, опущенным па нее из точки С', расположена точка с'. Такой чертеж назовем перспективой. При взгляде сверху на предметную плоскость (рис. IV. 25,6) мы видим прямую Т_к, в которую спроецировалась картинная плоскость, точку стояния с и на одном перпендикуляре с ней к прямой Т_к точку с' — основание главной точки. Полученное изображение является горизонтальной проекцией (планом). В дальнейшем при построении перспективы будем пользоваться такими разобщенными чертежами.

Проецирующие прямые и плоскости.Чтобы построить перспективу какой-либо точки, надо провести через нее проецирующую прямую и определить точку ее пересечения с плоскостью К. Для построения перспективы прямой следует провести через нее проецирующую плоскость (т.е. плоскость, проходящую через точку С) и найти линию пересечения этой плоскости с плоскостью К. Линию пересечения проецирующей плоскости с плоскостью К будем называть картинным следом плоскости, а линию пересечения такой плоскости с плоскостью Т— ее предметным следом. Все проецирующие плоскости, перпендикулярные плоскости Т, назовем предметно-проецирующими, перпендикулярные плоскости К — картинно-проецирующими, все остальные — проецирующими плоскостями общего положения.

По рис. IV. 26, а видно, что все предметно-проецирующие плоскости пересекаются между собой по прямой Сс, их предметные следы проходят через точку с, а картинные — перпендикулярны прямой Т_к. Если известен предметный след R_Т плоскости R, то, определив по горизонтальной проекции положение точки 1 (рис. IV.26,б), можно перенести ее в перспективу (рис. IV.26,в) на расстояние с'1 от точки с' и провести через нее картинный след перпендикулярно прямой Т_к. Если точка (например, точка А) лежит на предметном следе проецирующей плоскости, то ее перспектива (точка А') расположена на картинном следе.

Все картинно-проецирующие плоскости пересекаются между собой по прямой Cс', называемой главным лучом (рис. IV.27,а). Их картинные следы сходятся в точке С', а предметные перпендикулярны прямой Т_к. Если известен предметный след Q_Т плоскости Q, то следует найти точку 1 (рис, IV, 27, б) по горизонтальной проекции, определить ее положение в перспективе (рис. IV.27,б) и через нее и точку С' провести картинный след Q_К, плоскости Q.

Пусть дана точка А, лежащая в плоскости Т (рис. IV,28). Для построения ее перспективы проведем через нее проецирующую прямую АС и заключим ее в две проецирующие плоскости R и Q (рис. IV. 28, а). Примем плоскость R предметно-проецирующей, а плоскость Q — картинно-проецирующей. Тогда след R_Т пройдет через точки А и с, а след Q_Т — через точку А перпендикулярно прямой Т_к. Найдя точки 1 и 2 пересечения следов R_Т и Q_Т с прямой Т_к (рис. IV.28,б), перенесем их в перспективу (рис. IV.28,в) и построим пересечение картинных следов R_К и Q_К , которое определит перспективу А' точки А. Если точка В расположена на некоторой высоте h над плоскостью Т (на рис. IV.28,а она не показана), то построения на горизонтальной проекции не изменятся. В перспективе же достаточно поднять основание картины на высоту точки В, иначе говоря, поднять плоскость Т до высоты точки В(рис. IV.28,в).

Умея строить перспективы точек, можно построить перспективу прямой, на которой они лежат. Например, если точки А и Вопределяют положение прямой линии, то достаточно найти перспективы А' и В' этих точек и соединить их прямой.

Для построения перспективы двух параллельных прямых АВ и DE, лежащих в плоскости Т надо заключить их в две проецирующие плоскости М и Р общего положения (рис. IV. 29, а), которые пересекаются по прямой CF, параллельной заданным прямым.

Так как прямые АВ и DE лежат в горизонтальной плоскости Т, то и прямая CF будет горизонтальна и пересечет плоскость Т в точке F, лежащей на горизонте. Точка F называется точкой схода перспектив горизонтальных параллельных прямых.

Перспективой отрезка прямой АВ является отрезок А'В', причем отрезок АВ лежит на предметном следе М_Т плоскости М, а отрезок А'В' — на картинном следе М_К этой плоскости. Сказанное относится не только к отрезку АВ, но и к любому другому отрезку, лежащему на предметном следе проецирующей плоскости. Следовательно, перспективой предметного следа проецирующей плоскости является ее картинный след. Предметные следы плоскостей Р и М параллельны, картинные сходятся в точке F. Таким образом, перспективой параллельных прямых являются пересекающиеся прямые.

Перспективой точки А является точка А', точки В — точка В'. Продлив отрезок АВ в направлении от картинной плоскости и взяв на нем точку /V (на чертеже не показана), можно построить ее перспективу, лежащую на продолжении отрезка А'В' в направлении к точке F. По мере удаления точки, лежащей на прямой, ее перспектива все более приближается к точке F. Через саму точку Fпроецирующий луч может пройти только в том случае, когда он будет параллельным прямой АВ. Следовательно, точка Fпредставляет собой перспективу бесконечно удаленной точки прямой АВ. Так как приведенные рассуждения справедливы и относительно прямой CD, перспективой бесконечно удаленной точки которой является та же точка F, ее можно считать перспективой бесконечно удаленных точек всех прямых, параллельных прямой АВ.

Перспективы различно расположенных прямых. Для построения перспективы горизонтальной прямой, подобно прямой АВ на рис. IV.29,а, надо провести через нее проецирующую плоскость и прямую CF, лежащую в этой плоскости и параллельную прямой АВ.

Рассмотрим построение перспективы прямой АВ. Для этого (см. рис. IV.29, а), опустив перпендикуляр из точки F на плоскость Т, найдем точку f - основание точки схода, лежащую на прямой Т_к и соединим ее с точкой с. Прямая cf параллельна прямой CF, а следовательно, и прямой АВ. Поэтому для построения перспективы прямой АВ необходимо провести прямую cf параллельно прямой АВ до пересечения с основанием картины Т_к в точке f (см. рис. IV.29,б). Отметим точку 1 пересечения прямой АВ соснованием картины Т_к. Перенесем точки 1 и f в перспективу (см. рис. IV.29,б). Восставив из точки f перпендикуляр к прямой Т_к до пересечения с горизонтом HH, получим точку F. Соединив точки 1 и F, найдем перспективу А'В' прямой АВ. Перспектива прямой DEможет быть построена с использованием уже найденной точки F. Отметим точку 2 пересечения прямых DE и Т_к, перенесем ее в перспективу и соединим с точкой F.

Если параллельные линии, лежащие в плоскости Т или параллельные ей, одновременно параллельны плоскости К, проецирующие плоскости пересекут плоскость К по прямым, параллельным основанию картины Т_к. Точкой схода прямых, перпендикулярных плоскости К, является точка С'.

Таким образом, прямые, лежащие в плоскости Т, можно разделить на следующие четыре группы (см. рис. IV.30):

1) прямые, перпендикулярные основанию картины. Их перспективы проходят через точку С'. Иначе говоря, главная точка С' является точкой схода всех прямых, лежащих в плоскости Т и перпендикулярных основанию картины (например, прямая, проходящая через точку 2);

2) прямые, проходящие через точку с. Их перспективы перпендикулярны основанию картины (прямая, проходящая через точку 3);

3) прямые, параллельные основанию картины. Их перспективы также параллельны основанию картины (прямая АВ);

4) прямые общего положения. Их перспективы проходят через точки пересечения прямых с основанием картины и точку схода, лежащую на горизонте (прямая, проходящая через точку 1).

Для наглядности эти линии показаны штриховыми, сплошными или штрихпунктирными как на прямоугольном чертеже (рис. IV. 30, а), так и в перспективе (рис. IV.30,б).

Если параллельные прямые, не параллельные плоскости Т, по мере удаления от зрителя поднимаются вверх (восходящие прямые), то точка их схода расположена выше горизонта. Если они при тех же условиях опускаются вниз (нисходящие прямые), то точка их схода расположена ниже горизонта.

Проецирующая плоскость, проходящая через вертикальную прямую, является предметно-проецирующей и, следовательно, пересекается с плоскостью К по вертикальной прямой. Таким образом, перспективой вертикальной прямой является также вертикальная прямая.

Выбор точки зрения и картинной плоскости. Точку зрения и картинную плоскость выбирают в соответствии с замыслом проектировщика. В зависимости от высоты точки зрения перспективы делят на три вида: с нормальным горизонтом (рис. IV. 31, а) — высота точки зрения 170...180 см в масштабе чертежа, по которому строят перспективу, что примерно соответствует высоте человеческого роста; с высоким горизонтом (рис. IV.31,б) — точка зрения выше всех точек изображаемого предмета; перспективы с низким горизонтом (рис. IV.31,б). В зависимости от угла между крайними проецирующими лучами перспективы называют нормальными и широкоугольными (нормальным считают угол зрения в пределах 30...35°). При построении перспективы высоких зданий следует угол между проецирующей прямой, проходящей через верхнюю точку здания, и ее проекцией на предметную плоскость принимать в пределах 25...30°.

В архитектурных перспективах положение точки зрения обычно определяется местом, откуда здание после окончания строительства будет рассматриваться наибольшим числом зрителей. Иногда точку зрения выбирают со стороны наиболее характерного фасада здания. Например, точку зрения для построения перспективы здания, план которого изображен на рис. IV.32, следует выбирать так, чтобы зритель мог видеть выступающую часть здания. Зададимся основанием точки зрения с₁ и, соединив ее с углами здания, измерим получившийся при этом угол зрения. В данном случае он оказался больше 30°. Проведя биссектрису угла Ас₁В, переместим по ней точку с₁, до положения с, когда угол зрения станет равным 30°. Основание картинной плоскости Т_кпроводим в любом месте перпендикулярно биссектрисе угла. По мере приближения прямой Т_к к точке с размер перспективы уменьшается, по мере удаления — увеличивается. Можно провести основание картины Т, так, чтобы оно пересекало проекцию здания. В месте пересечения здания картиной его изображение имеет натуральный размер, поэтому, когда Т_к проходит через угол здания, для построения перспективы удобно брать все отметки по высоте с фасада здания и отмечать их на вертикали этого угла.

Построение перспективы плоской фигуры. Пусть даны точка С, заданная точкой с и высотой h, прямая Т_к и плоская фигура, лежащая в предметной плоскости (рис. IV.33). Требуется построить перспективу этой фигуры.

Воспользуемся различными комбинациями проецирующих плоскостей. Заключим прямые АВ, DE и КМ в проецирующие плоскости общего положения и отметим точки 1, 2 и 3 пересечения их предметных следов с основанием картины Т_к. Проведем через точку спрямую параллельно прямым AВ, DE и КМ и отметим точку f₁ ее пересечения с прямой Т_к. Перенеся точки 1, 2, 3 и f₁ в перспективу, определим точку F₁, а затем соединим ее с точками 1, 2 и 3. Проведя через прямые AM, КЕ и BD другую группу проецирующих плоскостей, найдем точки 4, 5, 6 и точку F₂. Соединив точки 4, 5, 6 с точкой F₂, на пересечении прямых 1F₁ и 4F₂ отметим точку А',на пересечении прямых 1F₁ и 6F₂ — точку В' и т.д.

Описанный выше способ построения перспективы называют способом точек схода перспектив доминирующих направлений параллельных линий или, короче, способом архитекторов. Построить перспективу можно и иначе. На рис. IV. 28 для построения перспективы точки А проводили через нее предметно-проецирующую и картинно-проецирующую плоскости.

Воспользуемся такими же плоскостями в данном примере (рис. IV.34). Строим перспективы отдельных точек путем проведения через них двух проецирующих плоскостей. Соединяем найденные перспективы точек прямыми линиями. Этот способ носит название способа следа луча. Он более трудоемок и менее точен, чем способ архитекторов, но оказывается удобным, когда точки схода далеко удалены за пределы чертежа.

Рис.

Иногда бывает необходимо комбинировать различные способы. Определим точку схода F₂ прямых AM, КE и BD (рис. IV.35). Определив способом следа луча перспективу точки Е, проведем через нее а затем направлении точки схода F₂. Перспективу точки К получим с помощью прямой Кс, проведенной на плане, перенесенной в перспективу. Для построения перспективы отрезка BDпродолжим его в плане до пересечения с основанием картины в точке 6 и, перенеся эту точку в перспективу, соединим ее с точкой схода F₂. Остальные построения ясны из чертежа. Описанный прием выгодно применять в тех случаях, когда одна из точек схода расположена далеко за пределами чертежа.

Масштаб высот. Допустим дана перспектива М' точки М, лежащей в плоскости Т, причем известно, что эта точка является концом отрезка NM (длиной h), перпендикулярного плоскости Т. Требуется найти перспективу точки N (рис. IV.37).

Проведем через точку М' перспективу произвольной горизонтальной прямой и отметим точки ее пересечения с горизонтом (точка F) и основанием картины (точка 2'). Отложив от точки 2' на перпендикуляре к прямой Т_к отрезок, равный h, получим точку 1'. Соединив точки 1' и F, проведем прямую M'N' как перпендикуляр из точки М' до пересечения с прямой 1'F в точке N'. Построения основаны на том, что прямые 1F и 2F горизонтальны и параллельны между собой (в перспективе они сходятся в точке F). Расстояние между ними измеряется отрезком NM, который в перспективе изображается перпендикулярным основанию картины Т_к. Отрезки 1—2 и NMв натуре равны, так как оба определяют расстояние между двумя параллельными прямыми (1F и 2F).

Если надо в точке Е (ее перспектива Е' задана), расположенной на плоскости Т и удаленной от основания картины Т_к на то же расстояние, что и точка М, построить перспективу вертикального отрезка DE, равного отрезку NM, то достаточно через точки М' и N'провести прямые, параллельные основанию картины, и из точки Е' восставить перпендикуляр до пересечения с прямой N'D'.Построения основаны на том, что прямые ND и ME в натуре параллельны. Для построения перспективы отрезка АВ, равного отрезку NM, если известна перспектива А' его верхней точки А, расположенной на той же высоте, что и точка N, следует провести через точку А' прямую, параллельную основанию картины Т_к, до пересечения с прямой 1'F и из полученной точки 3' опустить перпендикуляр на основание картины до пересечения с прямой 2'F в точке 4'. Из точки 4' надо провести прямую, параллельную прямой A'3' до пересечения с перпендикуляром, проведенным из точки А' к предметной плоскости в точке В'.

Треугольник 1'F2' называется боковым масштабом, позволяющим строить перспективы вертикальных отрезков любой величины, если известна высота хотя бы одной точки отрезка. Пусть требуется построить перспективу отрезка UL, когда известны перспектива L' точки L, лежащей в плоскости Т, и размер отрезка т. На прямой 1'—2' от точки 2' отложим отрезок 2'—5' длиной т и соединим точки 5' и F. Затем проведем через точку L' прямую, параллельную Т_к, до пересечения с прямой 2' F в точке 6'; из точки 6' построим вертикальную прямую, которая пересекается с прямой 5'F в точке 7'. Проведя через точку 7' прямую, параллельную основанию картины Т_к, отметим точку U' ее пересечения с перпендикуляром, восставленным из точки L'.

Если бы отрезок лежал в плоскости К, то в перспективе он проектировался бы в натуральный размер.

Перспектива тел. Построим перспективу схематизированного здания, заданного в проекциях (рис. IV.38,а).

Определив точки cxoда F₁ и F₂, построим перспективу основания здания АВDЕ, лежащего в плоскости Т (рис. IV.38,б). Далее рассмотренным выше приемом (см. рис. IV.38) найдем размер перспективы ребра боковой стены здания АТ, высота которого равна h. Проведя через концы отрезка А'Т' прямые Т'F₁ и Т'F₂, определим на пересечении их с вертикальными прямыми, проведенными через точки В' и Е', перспективы верхних концов ребер здания BN и ЕМ точки N' и М'. Перспективу точки L можно получить, найдя перспективу ее прямоугольной проекции на плоскости Т и отложив высоту с помощью бокового масштаба. В данном случае поступим иначе. Построим прямые N'M' и K'T' — перспективы диагоналей верхнего прямоугольника (NKMT) здания — и через точку 3' ихпересечения проведем прямую 3'F₁ до пересечения с прямой Т'M' в точке 4'. Отложив на вертикальной прямой, проходящей через точку 2' высоту точки L — отрезок 2'—5', соединим точки 5' и F₂, и отметим точку 6' пересечения прямой 5'F₂ с вертикальной прямой проходящей через точку 4'. Соединив точки 6' и F₁, найдем на прямой 6'F₁ точки L' и R', использовав для этого прямые с7 и с8, проведенные на плане здания (рис. IV. 38, а), а затем перенесенные в перспективу (вертикальные прямые, проходящие через точки 7' и 8'). Описанный прием удобен при построении перспективы зданий сложной конфигурации в плане.