Расчет значений целевой функции
| № | Представление особи | Фенотип, x | Значение целевой функции, f(x) = a + bx + cx2 + dx3 | |
| битовое | десятичное | |||
| Родители | ||||
| -8186 | ||||
| -12407 | ||||
| -6 | -1355 | |||
| Потомки | ||||
| -2327 | ||||
| -13802 | ||||
| -14080 | ||||
Таким образом, по результатам первой итерации для дальнейшего поиска оптимального решения (второй итерации) получена следующая популяция (табл. 14).
Таблица 14
Популяция после редукции
| № | Представление особи | Фенотип, x | Значение целевой функции, f(x) = a + bx + cx2 + dx3 | |
| битовое | десятичное | |||
| -6 | -1355 | |||
| -2327 | ||||
За одну итерацию качество популяции значительно возросло. Если в исходной популяции среднее значение целевой функции было -4811, а ее минимальное значение составляло -12407, то в популяции после первой итерации среднее значение возросло до 1034, а минимальное значение составило -2327. Лучшее (максимальное) значение увеличилось с 2704 до 5113 при оптимальном решении 20218 (см. аналитическое решение).
Задание на выполнение работы
Разработать программу, реализующую генетический алгоритм поиска максимального и минимального значений целевой функции f(x) = a + bx + + cx2 + dx3 в интервале x Î [-10, 53].
А. Индивидуальный вариант выбрать согласно табл. 15. Остальные параметры алгоритма принять такими же, как и в рассмотренном выше примере.
Таблица 15
Варианты заданий
| № варианта | a | b | c | d | № варианта | a | b | c | d |
| -40 | -1 | -86 | |||||||
| -50 | -55 | -38 | -71 | ||||||
| -20 | -40 | -96 | -67 | ||||||
| -5 | -3 | -45 | -63 | ||||||
| -5 | -26 | -84 | |||||||
| -63 | -25 | -93 | |||||||
| -80 | -64 | -66 | |||||||
| -8 | -40 | -28 | -64 | ||||||
| -26 | -33 | -82 | |||||||
| -86 | -59 | -57 | -97 | ||||||
| -63 | -2 | -111 | |||||||
| -120 | -68 |
Б.Отчет должен содержать:
· титульный лист;
· краткое описание задания, включая номер задания и коэффициенты целевой функции;
· расчет максимальных и минимальных значений целевой функции (включая граничные точки), выполненный с помощью методов математического анализа. Для контроля расчетов привести график функции
(см. рис. 41);
· расчеты с помощью генетического алгоритма при определении максимального значения целевой функции:
o первые две итерации работы программы (см. табл. 11–13);
o конечную популяцию (см. табл. 14) после 50 итераций и лучшую особь с максимальным значением целевой функции;
· расчеты с помощью генетического алгоритма при определении минимального значения целевой функции:
o первые две итерации работы программы (см. табл. 11–13);
o конечную популяцию (см. табл. 14) после 50 итераций и лучшую особь с минимальным значением целевой функции;
· текст программы;
· выводы.
Контрольные вопросы
1. Перечислите генетические операторы и их назначение.
2. Какие из генетических операторов выполняются с использованием элементов случайности, а какие – по строго детерминированным правилам?
3. Перечислите основные отличия генетических алгоритмов от традиционных методов поиска решений.
4. Опишите схему работы генетического алгоритма.
5. Что может являться критерием остановки работы генетического алгоритма?
ИСКУССТВЕННЫЕ НЕЙРОННЫЕ СЕТИ
Распознавание образов
Распознавание образов – научное направление, связанное с разработкой принципов и построением систем, предназначенных для определения принадлежности объекта к одному из классов объектов [6]. Классы объектов могут быть заранее выделены (задача классификации) или необходимо их выявить в процессе решения задачи (задача кластеризации). При этом под объектами могут пониматься не только осязаемые органами чувств различные предметы, но и явления, процессы, ситуации, сигналы и т. п.
Одним из наиболее эффективных и распространенных способов решения задач распознавания образов являются искусственные нейронные сети. Искусственная нейронная сеть – математическая модель, а также её программное или аппаратное воплощение, построенная по принципу организации и функционирования биологических нейронных сетей.
Базовым элементом искусственных нейронных систем является искусственный нейрон. Его обобщенная математическая модель выглядит следующим образом (рис. 42) [1].
|
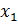 |
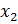 |
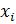 |
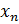 |
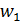 |
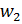 |
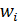 |
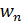 |
| f(P) |
Рис. 42. Математическая модель нейрона: входные сигналы 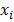 – данные, поступающие из окружающей среды или от других активных нейронов; вещественные весовые коэффициенты
– данные, поступающие из окружающей среды или от других активных нейронов; вещественные весовые коэффициенты 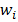 – определяют силу связи между нейронами; уровень активации (потенциал) нейрона
– определяют силу связи между нейронами; уровень активации (потенциал) нейрона 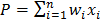 ; функция активации f(P) – предназначена для вычисления выходного значения сигнала, передаваемого другим нейронам
; функция активации f(P) – предназначена для вычисления выходного значения сигнала, передаваемого другим нейронам
Искусственная нейронная сеть состоит из нескольких слоев, в которые группируются нейроны (рис. 43).
На нейроны входного слоя подаются измеренные и преобразованные значения характеристик объекта (образа). Сигналы, поступившие к нейронам входного слоя, передаются на следующий слой (скрытый или выходной) без преобразования (т. е. к ним не применяется функция активации). Скрытые слои и выходной слой, отражающие специфику знаний, преобразуют входные данные. Выходной слой генерируют скаляр (одно значение) или вектор (несколько значений), являющийся решением задачи.
| Вектор входных сигналов | Входной слой | Скрытый слой | Скрытый слой | Выходной слой | Вектор выходных сигналов |
Рис. 43. Искусственная нейронная сеть с прямыми связями
В зависимости от количества преобразующих слоев (скрытых и выходного) различают одно- (в сети отсутствуют скрытые слои) и многослойные сети.
В качестве функций активации используются различные функциональные зависимости: линейная, пороговая, гиперболический тангенс, арктангенс, гауссиана и т. д. Одной из наиболее распространенных является сигмоидальная функция:
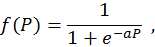
где a – коэффициент; e – основание натурального логарифма.
В зависимости от типа межнейронных связей различают искусственные нейронные сети:
· с прямыми связями (см. рис. 43);
· с перекрестными связями (рис. 44);
Рис. 44. Искусственная нейронная сеть с перекрестными связями
· с обратными (рекуррентными) связями (рис. 45). В таких сетях нейрон может посылать сигналы сам себе, нейронам того же слоя или нейронам предыдущих слоев.
Рис. 45. Искусственная нейронная сеть с обратными связями
Процедура построения искусственных нейронных сетей, используемых в задачах классификации, включает в себя насколько этапов.
Этап 1. Определение типа распознаваемых образов (фотография, видео, совокупность числовых характеристик и т. п.), набора измеряемых параметров образов, информативных с точки зрения распознавания, и классов распознаваемых образов.
Этап 2. Выбор способа преобразования (применение фильтров, подавление шумов, сегментация и т. п.) измеряемых параметров образов во входной вектор числовых величин и представления набора классов образов в виде вектора выходных величин. Эффективность нейросетевой модели повышается, если диапазоны изменения величин входного и выходного векторов будут нормализованы, например, в диапазоне [0,1] или [-1,1].
Этап 3. Проектирование архитектуры искусственной нейронной сети:
· определение количества слоев. В сети должно быть, как минимум, два слоя: входной и выходной. Количество скрытых слоев определяется, как правило, экспертным или опытным путем;
· определение количества нейронов в каждом слое. Количество нейронов во входном слое соответствует количеству преобразованных измеряемых параметров распознаваемых образов. Количество нейронов в выходном слое, как правило, соответствует количеству классов распознаваемых образов. Определение количества нейронов в каждом скрытом слое является неформальной проблемой, при решении которой можно использовать эвристическое правило: число нейронов в следующем слое должно быть в два раза меньше, чем в предыдущем;
· выбор типа связей между нейронами. Зависит от специфики решаемой задачи;
· выбор функции активации. Зависит от специфики решаемой задачи.
Этап 4. Обучение сети – уточнение значений весовых коэффициентов связей на основе многократного прогона обучающих примеров через сеть. Каждому обучающему примеру (образу) соответствуют строго определенные вектора входных и выходных величин. Обучающие примеры, как правило, представляют собой эталонные (идеальные) представления образов, а также их незначительные модификации. Они должны быть подобраны для каждого класса образов. Существует эмпирическое правило, которое устанавливает рекомендуемое соотношение l между количеством обучающих примеров и числом связей в нейронной сети: l ≤ 10 [7].
Этап 5. Тестирование сети с помощью контрольного набора примеров (образов) для оценки качества выбранной архитектуры и степени обучения. Контрольный набор должен содержать, как минимум, по одному примеру для каждого класса образов и включать в себя как эталонные, так и значительно искаженные образы.
Этапы с третьего по пятый могут совместно применяться для уточнения архитектуры сети на основе конструктивного или деструктивного подхода. В соответствии с первым подходом обучение начинается на сети небольшого размера, который постепенно увеличивается до достижения требуемой точности по результатам тестирования. Деструктивный подход базируется на принципе «прореживания дерева», в соответствии с которым из сети с заведомо избыточным объемом постепенно удаляют «лишние» слои, нейроны и примыкающие к ним связи. Этот подход дает возможность исследовать влияние удаляемых элементов на точность распознавания сети.
Процедура обучения является одной из ключевых при разработке и настройке сети. Существует большое количество подходов (правил) и соответствующих им методов (алгоритмов) обучения:
· правило коррекции по ошибке (дельта-правило);
· правило обратного распространения ошибки;
· синхронное обучение (правило Хебба);
· конкурентное обучение (правило Кохонена);
· правило Больцмана;
· и т. д.
Применение того или иного правила (алгоритма) зависит от выбранной архитектуры нейронной сети (количество слоев, тип связей, функция активации и т. п.).
Для решения задачи принадлежности предъявленного образа одному из заранее выделенных классов образов хорошо себя зарекомендовали многослойные нейронные сети с прямыми связями. Самым известным и популярным методом их обучения является алгоритм обратного распространения ошибки, который является модификацией классического метода градиентного спуска. Помимо многослойности и прямых связей, дополнительное требование его применимости – функция активации должна быть дифференцируема, т. е. иметь первую производную.
Алгоритм обратного распространения ошибки подразумевает два потока сигналов (данных) при прогоне одного обучающего образа через сеть:
· прямой (от входного до выходного слоя) – распространение сигнала, соответствующего значениям входного вектора обучающего образа;
· обратный (от выходного до входного слоя) – распространение сигнала ошибки для корректировки весовых коэффициентов связей.
Блок-схема алгоритма обратного распространения ошибки показана на рис. 46 со следующими обозначениями:
· э – номер эпохи;
· о – номер обучающего образа;
· с – номер слоя;
· нс – номер нейрона в слое с;
· NЭ – количество эпох;
· NО – количество обучающих образов;
· NС – количество слоев;
· NНс – количество нейронов в слое с;
· 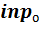 – вектор входных значений обучающего образа о;
– вектор входных значений обучающего образа о;
· 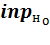 – значение элемента н входного вектора обучающего образа о;
– значение элемента н входного вектора обучающего образа о;
· 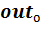 – вектор ожидаемых выходных значений обучающего образа о;
– вектор ожидаемых выходных значений обучающего образа о;
· 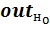 – значение элемента н выходного вектора обучающего образа о;
– значение элемента н выходного вектора обучающего образа о;
· 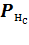 – потенциал нейрона н слоя с;
– потенциал нейрона н слоя с;
· 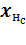 – выход нейрона н слоя с. Для нейронов входного слоя равен соответствующему элементу вектора входных значений
– выход нейрона н слоя с. Для нейронов входного слоя равен соответствующему элементу вектора входных значений 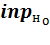 , для остальных слоев – результату расчета функции активации
, для остальных слоев – результату расчета функции активации 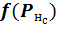 ;
;
· 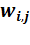 – весовой коэффициент связи нейрона i предыдущего слоя и нейрона j последующего слоя;
– весовой коэффициент связи нейрона i предыдущего слоя и нейрона j последующего слоя;
· 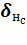 – ошибка (сигнал ошибки) нейрона н слоя с;
– ошибка (сигнал ошибки) нейрона н слоя с;
· 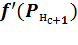 – результат расчета первой производной функции активации нейрона н слоя с+1;
– результат расчета первой производной функции активации нейрона н слоя с+1;
· 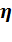 – норма обучения.
– норма обучения.
Перед процедурой обучения весовые коэффициенты всех связей инициализируются случайными малыми значениями (например, в диапазоне [-0.3, 0.3]).
| Начало |
Инициализация весовых коэффициентов всех связей сети случайными значениями 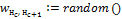 |
Для каждой эпох 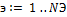 |
Для каждого обучающего образа 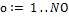 |
Инициализация (чтение) входного 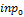 и выходного и выходного 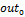 векторов образа векторов образа |
Присвоение значений входного вектора нейронам первого слоя 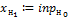 |
Для каждого последующего слоя 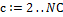 Для каждого последующего слоя Для каждого последующего слоя 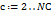 |
Для каждого нейрона слоя 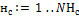 Для каждого нейрона слоя Для каждого нейрона слоя 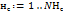 |
Расчет потенциала по всем входящим связям нейрона 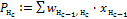 Расчет потенциала по всем входящим связям нейрона Расчет потенциала по всем входящим связям нейрона 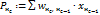 |
Расчет выхода нейрона 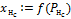 Расчет выхода нейрона Расчет выхода нейрона 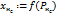 |
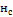 |
 |
Для каждого нейрона последнего слоя 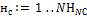 Для каждого нейрона последнего слоя Для каждого нейрона последнего слоя 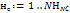 |
Расчет ошибки 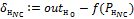 |
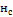 |
Для каждого промежуточного слоя 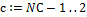 Для каждого последующего слоя Для каждого последующего слоя 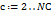 |
Для каждого нейрона слоя 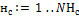 Для каждого нейрона слоя Для каждого нейрона слоя 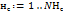 |
Расчет ошибки по всем исходящим связям нейрона 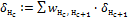 Расчет ошибки Расчет ошибки 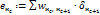 |
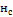 |
 |
Коррекция весовых коэффициентов всех связей сети 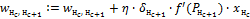 |
 |
 |
| Конец |
Рис. 46. Блок-схема алгоритма обратного распространения ошибки
При прогоне через сеть одного обучающего образа выполняется коррекция весовых коэффициентов. Прогон всех обучающих образов называется эпохой. Для настройки весовых коэффициентов (обучения) сети должно пройти достаточно большое количество эпох (несколько сотен, тысяч и т. п. – в зависимости от масштабов сети). Количество эпох может быть определено автоматически по заданной максимальной разнице средней ошибки (погрешности) между текущей эпохой и предыдущей, задано экспертом (как на рис. 46) и т. п.
При прямом распространении сигнала выполняется стандартная процедура, как и при распознавании образа:
· нейронам первого (входного) слоя присваиваются значения входного вектора 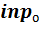 без преобразования. Можно условно принять, что эти значения
без преобразования. Можно условно принять, что эти значения 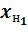 являются одновременно потенциалами
являются одновременно потенциалами 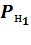 и выходами
и выходами 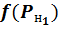 нейронов. Ввиду отсутствия преобразования при подсчете количества слоев
нейронов. Ввиду отсутствия преобразования при подсчете количества слоев
сети входной слой не учитывается и на схемах эти нейроны часто отображают иначе, чем остальные;
· для нейронов промежуточных и выходного слоев с учетом текущих значений весовых коэффициентов сети выполняется расчет потенциала 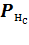 и выхода
и выхода 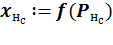 .
.
При проходе слоев в обратном направлении выполняется расчет сигнала ошибки:
· для нейронов последнего (выходного) слоя как разница между ожидаемым для образа значением выхода и полученным:
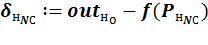 ;
;
· для нейронов промежуточных слоев с учетом весовых коэффициентов связей с нейронами последующего слоя и их сигналов ошибки:
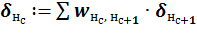 .
.
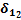 |
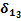 |
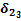 |
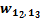 |
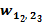 |
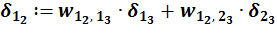 .
.
Рис. 47. Пример расчета сигнала ошибки для нейрона 1 слоя 2
Заключительной операцией является корректировка весовых коэффициентов всех связей на величину:
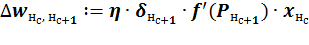 ,
,
где 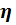 – норма обучения;
– норма обучения; 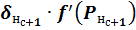 – локальный градиент. Произведение сигнала ошибки и результата расчета первой производной функции активации для нейрона, в который входит связь;
– локальный градиент. Произведение сигнала ошибки и результата расчета первой производной функции активации для нейрона, в который входит связь; 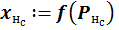 – результат расчета функции активации для нейрона, из которого выходит связь.
– результат расчета функции активации для нейрона, из которого выходит связь.
Норма обучения 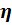 – коэффициент, от которого зависит величина изменения веса (скорость обучения). Выбирается в диапазоне 0 <
– коэффициент, от которого зависит величина изменения веса (скорость обучения). Выбирается в диапазоне 0 < 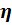 < 1.
< 1.
Значения потенциалов 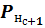 и
и 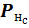 принимаются полученными при прямом распространении сигнала. В связи с этим корректировка весовых коэффициентов может выполняться независимо и в любом направлении (прямом или обратном).
принимаются полученными при прямом распространении сигнала. В связи с этим корректировка весовых коэффициентов может выполняться независимо и в любом направлении (прямом или обратном).
6.2. Лабораторная работа № 10. Распознавание образов
с использованием искусственной нейронной сети
Цель работы:освоение методов распознавания образов на базе искусственных нейронных сетей.
Рекомендации по выполнению работы
А. Описание задачи
На основе предъявленного образа (графического файла) требуется автоматическое определение цифры, изображенной в файле.
Поэтапно процедура разработки и обучения сети выглядит следующим образом.
Этап 1. Определение характеристик распознаваемых образов:
· тип распознаваемых образов – растровый графический файл;
· набор измеряемых параметров образов – образ задается совокупностью пикселей, каждый из которых характеризуется интенсивностью красного, зеленого и синего цветов (модель RGB);
· классы распознаваемых образов – цифры от 0 до 9 (10 классов).
Этап 2. Изображение, находящееся в файле, можно пропустить через «черно-белый» фильтр, разбить на стандартное количество одинаковых сегментов (например, заданных матрицей 8 × 10) и определить для каждого сегмента преобладающий цвет (черный или белый).
Таким образом, вектор входных величин сети для отдельного распознаваемого образа (файла) будет состоять из одного и того же количества элементов (8 × 10 = 80 элементов), каждый из которых может принимать значения: 1 (цвет сегмента черный) или 0 (цвет сегмента белый).
 |  | ||||||||
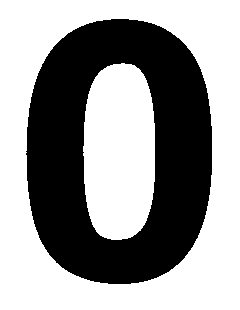 | |||||||||
Рис. 48. Преобразование исходного образа
Количество элементов вектора выходных величин будет соответствовать количеству классов распознаваемых образов. Значения элементов вектора нормализованы и равны 1 (признак принадлежности к классу) или 0 (в противном случае).
Этап 3. Проектирование архитектуры искусственной нейронной сети:
· количество слоев – 3;
· количество нейронов в слое:
o входном – 80;
o промежуточном – 40;
o выходном – 10;
· тип связей между нейронами – прямые;
· функция активации – сигмоидальная 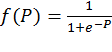 .
.
· первая производная функции активации – 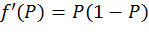 .
.
Этап 4. Обучение сети выполняется с помощью алгоритма с обратным распространением ошибки.
Для обучения экспертом приготовлено 20 обучающих образов – по два на каждый класс (цифру), один из которых эталонный (идеальный) и один с незначительной модификацией. Каждый образ характеризуется строго определенными векторами входных и выходных величин. Вектор входных величин соответствует преобразованному обучающему образу (файлу) и состоит из 80 элементов, значения которых 0 или 1 согласно цвету сегмента. Вектор выходных величин соответствует классу, которому принадлежит образ, и состоит из 10 элементов, значения которых равны 1 или 0. Так, для обучающего образа цифры «0» вектор выходных величин –
[1, 0, 0, 0, 0, 0, 0, 0, 0, 0].
Перед процедурой обучения весовые коэффициенты всех связей инициализируются малыми случайными значениями в диапазоне [-0.3, 0.3].
При обучении все 20 образов последовательно прогоняются через сеть с корректировкой весовых коэффициентов после прогона каждого образа. Данная процедура повторяется 500 раз (количество эпох – 500). Норма обучения принята равной 0.1.
Этап 5. Тестирование сети выполняется с помощью контрольных образов. Например, если на вход сети был подан образ цифры «2», а на выходе получен вектор [0 0.11 0.76 0.23 0.01 0.05 0 0 0 0.25], то распознавание прошло успешно.
Задание на выполнение работы
Разработать программу «Распознавание образов», отвечающую следующим требованиям.
А. Распознавание образов должно выполняться искусственной нейронной сетью, обучаемой по алгоритму с обратным распространением ошибки. Общие требования к сети и программе:
· связи между нейронами – прямые;
· количество скрытых слоев – 1;
· количество нейронов выходного слоя (классов образов) – не менее 4;
· количество обучающих образов – не менее 1 на каждый класс образов;
· функция активации – сигмоидальная 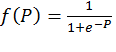 ;
;
· распознаваемые (тестовые) образы – формируются пользователем;
· норма обучения и количество эпох обучения – задаются пользователем;
· режим обучения или распознавания – задается пользователем.
Примерный интерфейс программы показан на рис. 49.
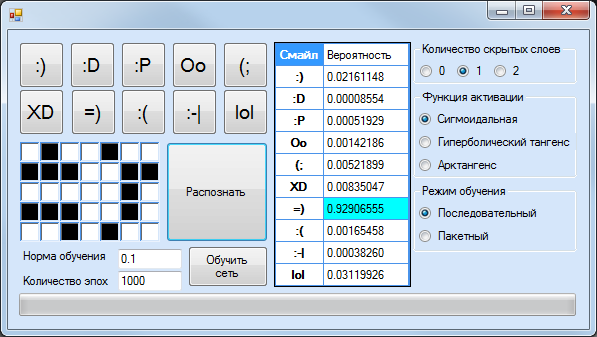
Рис. 49. Программа «Искусственная нейронная сеть»[15]
Б. Индивидуальный вариант выбрать согласно табл. 16.
Таблица 16
Варианты заданий на выполнение лабораторной работы
| № варианта | Тип образа | Количество нейронов скрытого слоя |
| Арабские цифры | ||
| Римские цифры | ||
| Буквы русского алфавита | ||
| Буквы латинского алфавита | ||
| Арифметические операции (+, -, /, *, Ö, % и т. д.) | ||
| Логические операции (Ú, Ù, &, Þ, ¯ и т. д.) | ||
| Операции сравнения (<, =, ³, º, » и т. д.) | ||
| Операции с множествами (Ç, È, Æ, Î и т. д.) | ||
| Цветочки | ||
| Виды транспорта | ||
| Машинки | ||
| Карточные масти |
Окончание табл. 16
| № варианта | Тип образа | Количество нейронов скрытого слоя |
| Птицы | ||
| Рыбы | ||
| Фрукты | ||
| Смайлики | ||
| Геометрические фигуры | ||
| Дорожные знаки | ||
| Виды заливки | ||
| Логотипы компаний | ||
| Знаки зодиака | ||
| Домино |
В.Отчет должен содержать:
· титульный лист;
· описание задания;
· вид 4 обучающих образцов и соответствующие им входные и выходные вектора с эталонными значениями;
· вид 4 тестовых (искаженных) образцов и соответствующие им входные и выходные вектора с расчетными значениями;
· текст программы;
· вывод.
Контрольные вопросы
1. Опишите строение биологического нейрона.
2. Опишите математическую модель нейрона.
3. Приведите классификацию искусственных нейронных сетей по типу нейронных связей.
4. Опишите процедуру построения искусственных нейронных сетей.
5. Назовите условия применимости алгоритма с обратным распространением ошибки при обучении искусственных нейронных сетей.
Заключение
Изложенный в пособии теоретический материал, а также лабораторные работы, являются наиболее популярными и перспективными направлениями в области искусственного интеллекта. Предоставление многочисленных сервисов в Интернете (поиск информации, контекстная реклама, перевод текстов, распознавание речевых запросов), игровая индустрия, системы информационной безопасности (выявление уязвимостей, угроз и атак) немыслимы без применения интеллектуальных методов обработки информации.
Разработка теории логики предикатов является дальнейшим развитием логики высказываний. Логика предикатов была принята в Японии за основу при создании компьютеров пятого поколения. Несмотря на фиаско проекта, он имел большой общественный резонанс и подтолкнул правительства других стран и международные корпорации к интенсификации исследований в области искусственного интеллекта. Поддерживаемые и продвигаемые консорциумом W3C онтологические модели представления информации должны вывести Интернет на новый уровень.
В настоящий момент искусственные нейронные сети переживают очередной всплеск интереса. Ежедневно в средствах массовой информации, научных и популярных изданиях сообщается о новых сферах их применения при решении теоретических проблем и практических задач. Нечеткие множества активно применяются в алгоритмах работы бытовой техники (холодильники, стиральные машины, печи). Генетические алгоритмы и эвристические методы стали незаменимым инструментом при решении оптимизационных производственных задач, где традиционные методы (математический анализ, математическое программирование) бессильны.
Обзор интеллектуальных методов, выполненный в пособии, должен сформировать у обучающихся представление о современных тенденциях в области искусственного интеллекта, а лабораторные работы – закрепить навыки их применения на практике.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Люггер Джордж Ф. Искусственный интеллект: стратегии и методы решения сложных проблем / Джордж Ф. Люггер. – М. : Вильямс, 2004. – 864 с.
2. Искусственный интеллект : справ. / под ред. Д.А. Поспелова.
в 3-х кн. Кн.2. Модели и методы. – М. : Радио и связь, 1990. – 304 с.
3. Вагнер, Г. Основы исследования операций. В 3 т. Т.2 / Г. Вагнер. – М. : Мир, 1972. – 488 с.
4. Представление и использование знаний / под ред. Уэно Х., Исидзука М. – М.: Мир, 1989. – 220 с.
5. Базы данных. Интеллектуальная обработка информации / В.В. Корнеев, А.Ф. Гареев, С.В. Васютин, В.В. Райх. – М. : Нолидж, 2001. – 496 с.
6. Старков, Ф.А. Распознавание образов : учеб. пособие / Ф.А. Старков, Е.Ф. Старков. – Курск : Изд-во Курского гуманитарно-техн. ин-та, 2000. – 140 с.
7. Андрейчиков А.В. Интеллектуальные информационные системы : учеб. / А.В. Андрейчиков, О.Н. Андрейчикова. – М. : Финансы и статистика, 2004. – 424 с.
8. Осуга, С. Обработка знаний / С. Осуга. – М. : Мир, 1989. – 293 с.
9. Приобретение знаний / под ред. С. Осуги, Ю. Саэки. – М. : Мир, 1990. – 304 с.
10. Лорьер Ж.-Л. Системы искусственного интеллекта / Ж.-Л. Лорьер. – М. : Мир, 1991. – 568 с.
11. Девятков, В.В. Системы искусственного интеллекта : учеб. пособие для вузов / В.В. Девятков. – М. : Изд-во МГТУ им. Н.Э.Баумана, 2001. – 352 с.
12. Стерлинг, Л. Искусство программирования на языке Пролог /
Л. Стерлинг, Э. Шапиро. – М. : Мир, 1990. – 235 с.
13. Малпас Дж. Реляционный язык Пролог и его применение /
Дж. Малпас. – М. : Наука, 1990. – 464 с.
14. Братко, И. Алгоритмы искусственного интеллекта на языке Prolog / И. Братко. – М. : Вильямс, 2004. – 640 с.
15. Лапшин, В.А. Онтология в компьютерных системах / В.А. Лапшин. – М. : Научный мир, 2010. – 224 с.
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ......................................................................................................... 3
1. ЛОГИКА ПРЕДИКАТОВ ПЕРВОГО ПОРЯДКА........................................ 5
1.1. Основы логики предикатов первого порядка.......................................... 5
1.2. Основы Пролога....................................................................................... 7
1.3. Назначение и основные возможности SWI-Prolog................................ 10
1.4. Лабораторная работа № 1. Представление фактов и правил в Прологе 13
1.5. Лабораторная работа № 2. Рекурсия в Прологе.................................. 16
1.6. Лабораторная работа № 3. Обработка списков в Прологе.................. 21
2. ОНТОЛОГИИ............................................................................................... 24
2.1. Онтологии и семантическая паутина...................................................... 24
2.2. Краткие сведения о спецификациях семантической паутины............... 27
2.3. Лабораторная работа № 4. Построение онтологической модели
в Protégé. Создание классов...................... 33
2.4. Лабораторная работа № 5. Построение онтологической модели
в Protégé. Создание экземпляров классов 39
2.5. Лабораторная работа № 6. Выполнение SPARQL-запросов в Protégé 42
3. ЭВРИСТИЧЕСКИЕ АЛГОРИТМЫ............................................................. 45
3.1. Методы поиска решений с использованием графов.............................. 45
3.2. Лабораторная работа № 7. Решение оптимизационной задачи
с использованием эвристического
алгоритма.................................................. 49
4. НЕЧЕТКИЕ МНОЖЕСТВА......................................................................... 56
4.1. Основы теории нечетких множеств и нечеткой логики......................... 56
4.2. Лабораторная работа № 8. Решение прикладной задачи
с использованием нечетких множеств...... 60
5. ГЕНЕТИЧЕСКИЕ АЛГОРИТМЫ................................................................ 64
5.1. Эволюционные вычисления.................................................................... 64
5.2. Лабораторная работа № 9. Решение оптимизационной задачи
с использованием генетического алгорит