Лабораторная работа № 2. Рекурсия в Прологе

Цель работы: освоение программирования на языке Пролог с использованием рекурсивных правил.

Рекомендации по выполнению работы

Рекурсия (в программировании) – алгоритмический метод, заключающийся в возможности обращения правила (функции, процедуры) к самому себе один или более раз.

В виду отсутствия в Прологе операторов цикла, рекурсия является часто используемым приемом в программах на этом языке. Любая рекурсивная процедура в Прологе должна включать, как минимум, два правила:

1) нерекурсивное правило, определяющее его вид в момент прекращения рекурсии;

2) рекурсивное правило. Первая подцель, вырабатывает новые значения аргументов, а вторая – вызов самого правила с новыми значениями аргументов.

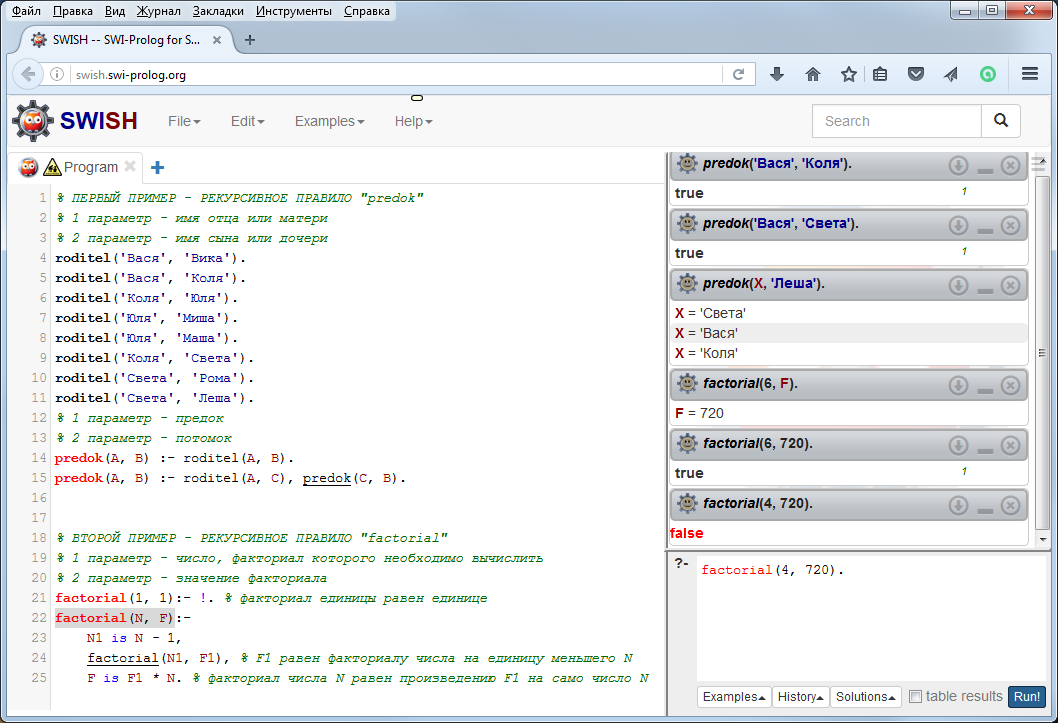
Рис. 5. Использование рекурсивных правил

В программе на рис. 5 приведены примеры двух предикатов с рекурсивными правилами:

· predok – предикат, позволяющий определить родственную связь «предок-потомок» через поколения. Первое (нерекурсивное) правило предиката predok предписывает Прологу завершить процедуру поиска предка (потомка), если первый терм является непосредственным родителем ребенка, указанного вторым термом. В противном случае срабатывает второе (рекурсивное) правило, предписывающее в процессе поиска связи между предполагаемыми предком и потомком добавить промежуточное поколение. На первый вопрос «Является ли Вася предком Коли?» получен положительный ответ, так как Вася является непосредственным родителем Коли. На второй вопрос «Является ли Вася предком Светы?» получен положительный ответ, так как Вася является дедушкой Светы. На третий вопрос «Кто является предком Леши?» получены три ответа: Света (мама), Вася (дедушка) и Коля (прадедушка);

· factorial – предикат, определяющий значение факториала для заданного числа. Первое (нерекурсивное) правило предиката factorial определяет для числа «1» значение факториала, равное «1». В противном случае от числа N, указанного в качестве первого терма, необходимо отнять единицу [N1 is N – 1], найти значение факториала F1 для нового числа N1 [factorial(N1, F1)], определить факториал для исходного числа N [F is F1 * N] и установить значение F в качестве второго терма.

При необходимости вычислений в программе следует учитывать разницу и особенности применения операций «=» и «is». Первая операция не приводит к вычислению (преобразованию) выражения, записанного справа от операции (вопрос 1 на рис. 6), а вторая – приводит (вопрос 2 на рис. 6).
В случае использования свободной переменной операции приводят к присваиванию исходного (преобразованного) выражения, записанного справа от операции (см. вопросы 1 и 2 на рис. 6). В случае использования связанной переменной выполняется сравнение левой и правой части. Так, на вопрос 3 (рис. 6) вначале свободной переменной X присваивается выражение «5+1», а затем для уже связанной переменной X выполняется сравнение с выражением «4+2» («5+1» = «4+2» ® false). На вопрос 4 (рис. 6) вначале свободной переменной X присваивается «6» (результат выражения «5+1»), а затем для уже связанной переменной X выполняется сравнение с «6» (результатом выражения «4+2») .

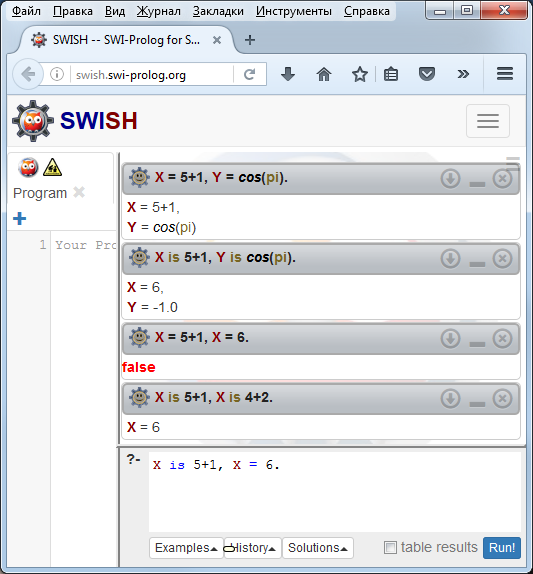
Рис. 6. Использование операций «=» и «is»

Задание на выполнение работы

Разработать программу расчета функции с использованием рекурсивных правил, отвечающую следующим требованиям.

A.Программа должна запрашивать у пользователя:

· N – количество членов ряда, учитываемых при расчете приближенного значения функции;

· X – значение переменной (если в формуле есть X).

Б. Выдавать результаты работы на экран:

· приближенное значение функции, рассчитанное с помощью ряда;

· точное значение функции, рассчитанное с помощью встроенных функций Пролога.

В.По индивидуальному заданию добавить в программу правила для определения приближенного значения функции с помощью ряда:

1)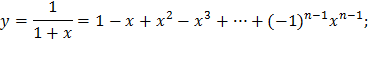
2)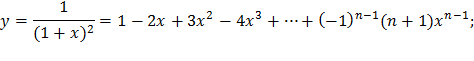
3)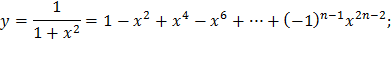
4)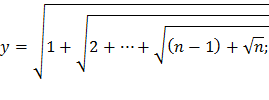
5)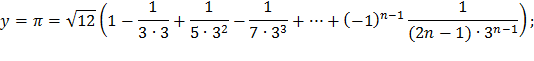
6)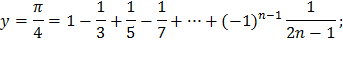
7)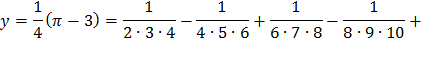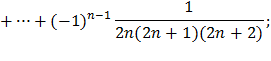
8)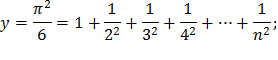
9)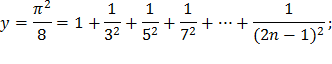
10)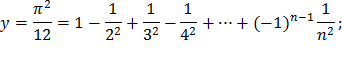
11)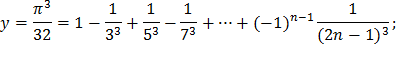
12)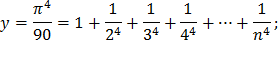
13)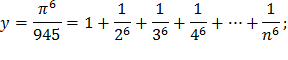
14)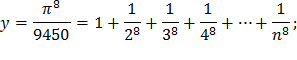
15)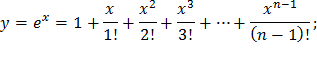
16)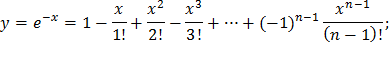
17)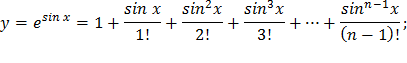
18)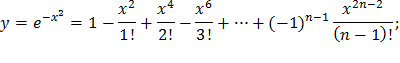
19)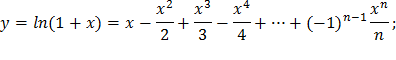
20)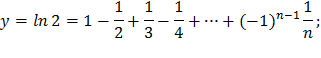
21)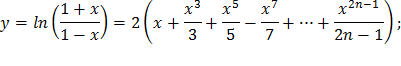
22)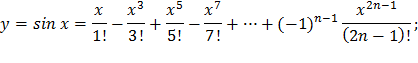
23)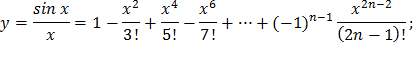
24)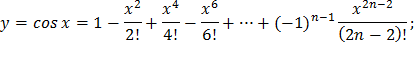
25)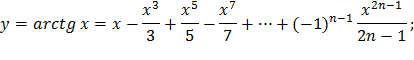
26)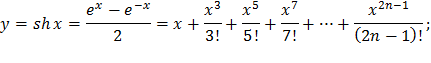
27)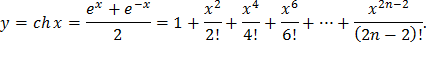

Г.Отчет должен содержать:

· титульный лист;

· описание задания;

· текст программы;

· вопросы с ответами, иллюстрирующие корректность работы программы;

· вывод.