Определение полуцикловых характеристик свойств материалов при одноосном растяжении до разрушения

Цель работы. Изучение методов и приборов для определения разрывных характеристик свойств искусственных кож и пленочных материалов.

Задания: 1.Вырезать образцы мягких искусственных кож на тканой и нетканой основах из рулона и подготовить их к испытанию.

2. Изучить особенности испытания искусственных кож на разрывной машине РТ-250М.

3. Провести испытания и рассчитать характеристики свойств мягких искусственных кож при одноосном растяжении.

Основные понятия

Одноосное растяжение в материале возникает тогда, когда внешние силы, действующие на материал вдоль одной оси, направлены в разные стороны.

Основными полуцикловыми характеристиками свойств материалов при одноосном растяжении являются:

абсолютное удлинение Δℓ, (мм) - изменение линейного размера рабочей части элементарной пробы материала при действии внешней силы:

Δℓ= ℓ₁- ℓ, (4.1)

где ℓ₁ - длина рабочей части элементарной пробы при действии внешней силы в момент ее разрушения; ℓ - длина рабочей части элементарной пробы до растяжения.

относительное удлинениеɛ(%) - относительное абсолютного удлинения к первоначальной длине рабочей части пробы:

ɛ = 100 (ℓ₁- ℓ)/ ℓ] = 100(Δℓ / ℓ); (4.2)

предел прочности σ (МПа или Па), напряжение возникающее в материале при действии внешней силы, представляет собой разрывное усилие, приходящееся на единицу площади поперечного сечения пробы:

σ = P_р/F, (4.3)

где Р_р – действующая разрывная сила, Н; F - площадь поперечного сечения рабочей части испытываемой элементарной пробы материала, м²;

F= b•h, (4.4)

где b - ширина, м; h - толщина, м;

прочность Р*(даН или Н) - максимальное значение силы Р_р, которое необходимо приложить к элементарной пробе материала для его разрушения.

Материалы, применяемые для производства изделий легкой промышленности, не подчиняются закону Гука, поэтому уравнение зависимости P*= f(Δℓ*) имеет вид степенной функции (рис. 4.1):

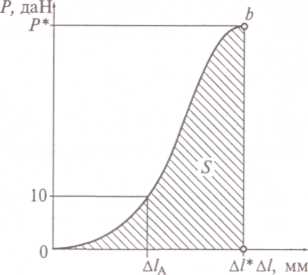Рис. 4.1.График растяжения пробы материала

ɛ = AQ^п (4.5)

где А - коэффициент растяжимости материала; Q - усилие, определяемое по формуле Q=0,1•Р*; где п - показатель степени.

Уравнение (4.5) описывает кривую растяжения материала только при действии на материал внешней силы Р* < 0,75Р_р.

Коэффициент растяжимости А для всех видов материалов определяется при действии на элементарную пробу силы Р=10 даН.

Относительная деформация ɛ при этой силе принимает значение ɛ_А, и, исходя из уравнения (4.5), ɛ_А численно равно А, так как при Q = 1 значение Q^п = 1. Для расчета ɛ_А из графика зависимости P*= f(Δℓ*) определяют величину абсолютного удлинения Δℓ_А при Р=10 даН (см. рис. 4.1). Зная Δℓ_А, относительную деформацию вычисляют по формуле:

ɛ_А =100• (Δℓ_А /ℓ). (4.6)

Если коэффициент растяжимости характеризует деформационные свойства материала при действии силы в 10 даН, то показатель степени п в уравнении (4.5) определяет изогнутость кривой относительно оси Δℓ и может принимать следующие значения: п > 1, п = 1, п < 1.

Показатель степени п можно рассчитать, если прологарифмировать (4.5):

lgɛ = lgА + n•lg Q.

Тогда

п = (lgɛ - lgА) / lg Q. (4.7)

Показатель степени п определяют как среднеарифметическое нескольких показателей степени п, рассчитанных при разных значениях Q и ɛ.

Показатель степени п можно определить и графическим способом. Зная величины lgɛ и lg Q, строят график зависимости lgɛ=f(lg Q). Тангенс угла наклона прямой к оси абсцисс равен показателю степени п, т. е. tgα =п.

Если показатель степени п не зависит от ширины испытываемой пробы, то коэффициент растяжимости материала А зависит от ширины испытываемой пробы. Если ширина пробы больше 10 мм, то коэффициент растяжимости материла А_b рассчитывают по следующей формуле:

А_b = А/ bⁿ (4.8)

где А — коэффициент растяжимости материла при b = 10 мм.

Характеристиками упругих свойств материалов при полуцикловых испытаниях являются:

условный модуль упругости Е_у (Па или МПа):

Е_у = 100 σ_у/ ɛ_у, (4.9)

где σ_у - условное напряжение; ɛ_у - условная относительная деформация материала; ɛ_у = 100(0,75 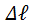/ℓ)

условная жесткость D_y(даН или Н) - способность материалов сохранять исходные размеры при действии внешней силы:

Dy=E_yF, (4.10)

где F- площадь поперечного сечения элементарной пробы.

Условную жесткость материала с учетом формул (4.9 и 4.10) и при σ_у = P_y/F, можно вычислить по формуле:

D_y= 100(P_y/ ɛ_у). (4.11)

Чем выше значения условного модуля упругости и жесткости, тем меньше деформация материала.

Характеристиками энергетических свойств материалов при полуцикловых испытаниях являются:

работа при разрыве A_R (Дж), равная площади S, расположенной под кривой графика растяжения пробы (рис. 4.1), и вычисляемая по формуле:

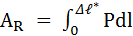; (4.12)

удельная работа при разрыве A_v (Дж/м³) или при растяжении A_m (Дж/кг), которая рассчитывается соответственно по формулам:

А_V=А_R/V; (4.13)

A_m = A_R/m, 4.14)

где V— объем рабочей зоны, который определяют как V= ℓ•F, где ℓ — длина, м; F— средняя площадь поперечного сечения, м²; т — масса рабочей части элементарной пробы, г.

Масса топределяется после разрушения пробы испытываемого материала. Для этого остатки испытанной элементарной пробы вынимают из зажимов разрывной машины и отрезают части пробы, которые находились в зажимах. Массу т определяют с точностью до 0,01 г.

Для характеристики равномерности (изотропности)механических свойств искож и пленок по площади пробы применяют коэффициент равномерности k_р:

k_р = П_min/П_max (4.17)

где П_тin и П_тах - среднеарифметическое значение соответственно минимального и максимального значений любого однотипного показателя: прочности (Р), относительного удлинения (ɛ), предела прочности (σ) и др.

Рассмотренные показатели механических свойств нормируются государственными стандартами на соответствующие виды материалов.