Сколько всего сотрудников в КБ?

2) Сколько из них знают только один язык?

3) Ровно 2 языка?

23. При обследовании читательских вкусов студентов оказалось, что 60% студентов читают журнал А, 50% - журнал В, 50% - журнал С, 30% - журналы А и В, 20% - журналы В и С, 40% - журналы А и С, 10% - журналы А, В и С. Сколько процентов студентов:

1) не читает ни одного из журналов;

2) читает в точности 2 журнала;

3) читает не менее 2 журналов?

24. На одной из кафедр университета работают 13 человек, причем каждый из них знает хотя бы один иностранный язык. 10 человек знают английский, 7 - немецкий, 6 - французский. 5 - английский и немецкий, 4 - английский и французский, 3 - немецкий и французский. Сколько человек знают:

1) все 3 языка?

2) ровно 2 языка?

3) только английский язык?

25. Сколько трехзначных чисел можно составить из цифр числа 12304122?

26. В лифт сели 8 человек. Сколькими способами они могут выйти из лифта на четырех этажах так, чтобы на каждом этаже вышел, по крайней мере, один человек?

27. Сколькими способами четыре игрока могут разделить 28 костей домино по 7 штук каждому?

28. Имеется 10 одинаковых ручек, 7 простых карандашей и 8 кисточек. Сколькими способами их можно разложить по двум коробкам? По трем коробкам?

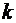29. Имеется предметов 1-го типа, предметов 2-го типа,…, – -оготипа. Сколькими способами их можно разделить между двумя людьми так, чтобы каждый получил не менее предметов 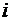-ого типа, ?

30. Имеется предметов 1-го типа, предметов 2-го типа,…, – 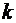-оготипа. Сколькими способами их можно разделить между 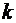лицами? Сколькими способами это можно сделать при условии, что каждый получит хотя бы по один предмет?

31. Сколько целых положительных решений имеет уравнение

?

32. Сколькими способами можно выбрать трех дежурных из группы в 20 человек?

33. Каким числом способов можно на обычной шахматной доске разместить белую и черную ладьи так, чтобы они не атаковали друг друга?

34. Лифт останавливается на десяти этажах. Сколькими способами могут распределиться между этими остановками 8 пассажиров, находящихся в кабине лифта?

35. Семь яблок и три апельсина надо положить в два пакета так, чтобы в каждом пакете был хотя бы один апельсин, и чтобы количество фруктов в них было одинаковым. Сколькими способами это можно сделать?

36. Лифт, в котором находится 9 пассажиров, может останавливаться на десяти этажах. Пассажиры выходят группами в два, три и четыре человека. Сколькими способами это может произойти?

37. Сколько существует семизначных чисел, у которых:

1) цифры различны, причем первая - не 9, а последняя - не 0?

2) ровно три цифры четные?

3) среди цифр имеется не менее двух четных?

4) среди цифр есть одинаковые?

5) сумма цифр четна?

38. Шесть ящиков различных материалов доставляют на восемь этажей стройки. Сколькими способами можно распределить материалы по этажам? В скольких из них на восьмой этаж будет доставлено не менее двух материалов?

39. Номер кодового замка состоит из двух букв и четырех цифр. Сколько различных номеров можно составить, используя 30 букв и 10 цифр?

40. Код замка состоит из пяти десятичных цифр. Известно, что среди них один раз встречается цифра 0 и дважды - цифра 3. Сколько комбинаций нужно перебрать, чтобы наверняка открыть замок?

41. Чему равна сумма четырехзначных чисел, полученных при всевозможных перестановках цифр

1) 2, 5, 5, 5;

2) 3, 7, 7, 5?

42. Сколько существует пятизначных чисел, у которых

1) цифры различны, причем первая – не 5, последняя – не 0;

2) среди цифр есть одинаковые;

3) цифры различны, причем 0 отсутствует, а цифры 2, 4, 5 встречаются одновременно;

4) среди цифр не менее двух четных?

43. Сколько чисел, меньших 10⁵, можно записать из цифр 2, 4, 5? Сколько среди них нечетных?

44. Сколько имеется различных треугольников, длины сторон которых принимают значения: 8, 10, 12 и 14 см? Сколько среди них равносторонних, равнобедренных и разносторонних?

45. Сколькими способами из шести пар перчаток различных размеров можно выбрать одну перчатку на левую руку и одну – на правую руку так, чтобы перчатки были разных размеров?

46. У одного студента 5 разных книг, у другого — 7 других книг. Сколькими способами студенты могут обменяться двумя книгами?

47. Сколькими способами можно выбрать на шахматной доске белый и черный квадраты, не лежащие на одной и той же горизонтали и вертикали?

48. Стороны каждой из двух игральных костей помечены числами 0, 1, 3, 7, 15, 31. Сколько различных сумм может получиться при метании этих костей?

49. Сколькими способами можно расставить 20 книг в книжном шкафу с пятью полками, если каждая полка может вместить все 20 книг?

50. Кидают шесть игральных костей (различимых друг от друга), помеченных числами 1, 2, 3, 4, 5, 6. В скольких случаях они дадут два вида очков?

51. Сколькими способами 3 человека могут разделить между собой 6 одинаковых яблок, 1 апельсин, 1 сливу, 1 лимон, 1 грушу, 1 персик и 1 айву?

Контрольные задания

1. Дано множество U из n элементов. Каким числом способов в нем можно выбрать три подмножества A, B, C так, чтобы выполнялись заданные условия?

1. 7, , ;

2. 9, , ;

3. 8, , ;

4. 7, , ;

5. 6, , ;

6. 7, , ;

7. 9, , ;

8. 7, , ;

9. 9, , ;

10. 8, , ;

11. 8, , ;

12. 7, , ;

13. 7, , ;

14. 8, , ;

15. 5, , ;

16. 6, , ;

17. 8, , ;

18. 7, , ;

19. 9, , ;

20. 6, , ;

21. 7, , ;

22. 8, , ;

23. 7, , ;

24. 9, , ;

25. 7, , ;

26. 6, , ;

27. 8, , ;

28. 8, , ;

29. 8, , ;

30. 7, , ;

31. 6, , ;

32. 7, , ;

33. 8, , ;

34. 6, , ;

35. 6, , ;

36. 7, , ;

37. 6, , ;

38. 7, , ;

39. 6, , ;

40. 8, , .

2. На одной из кафедр университета работают S человек, среди которых T человек не знают ни одного иностранного языка. A человек знают английский, N – немецкий, F – французский. AN знают английский и немецкий, AF – английский и французский, NF – немецкий и французский, ANF знают все три языка. По заданным в таблице условиям восстановить недостающую информацию.

№	S	A	N	F	AN	AF	NF	ANF	T
1.									?
2.		?
3.				?
4.								?
5.	?
6.						?
7.			?
8.					?
9.									?
10.		?
11.				?
12.								?
13.	?
14.						?
15.			?
16.					?
17.									?
№	S	A	N	F	AN	AF	NF	ANF	T
18.	?
19.		?
20.							?
21.				?
22.								?
23.						?
24.			?
25.					?
26.									?
27.	?
28.		?
29.				?
30.						?
31.								?
32.							?
33.									?
34.			?
35.					?
36.	?
37.				?
38.		?
39.						?
40.								?

3. Рассматриваются слова в алфавите . Через обозначается число вхождений буквы в слово. Требуется подсчитать число слов длины n, удовлетворяющих данным условиям.

1. 3, 9, ;

2. 4, 7, ;

3. 4, 7, ;

4. 5, 8, ;

5. 3, 9, ;

6. 5, 7, ;

7. 3, 7, ;

8. 3, 10, ;

9. 3, 7, ;

10. 4, 6, ;

11. 4, 5, ;

12. 3, 8, ;

13. 3, 8, ;

14. 3, 6, ;

15. 4, 7, ;

16. 5, 8, ;

17. 4, 6, ;

18. 4, 8, ;

19. 4, 9, ;

20. 5, 6, ;

21. 5, 6, ;

22. 4, 8, ;

23. 5, 7, ;

24. 4, 8, ;

25. 5, 7, ;

26. 4, 7, ;

27. 5, 6, ;

28. 5, 7, ;

29. 4, 8, ;

30. 3, 9, ;

31. 4, 7, ;

32. 4, 7, ;

33. 5, 6, ;

34. 3, 8, ;

35. 4, 8, ;

36. 5, 8, ;

37. 4, 8, ;

38. 3, 9, ;

39. 3, 9, ;

40. 5, 7, , .

4. Сколькими способами можно переставить буквы слова:

1. «здание», чтобы гласные шли в алфавитном порядке;

2. «перешеек», чтобы четыре буквы «е» не шли подряд;

3. «ежевика», чтобы «и» шла непосредственно после «к»;

4. «тарантас», чтобы две буквы «а» не шли подряд;

5. «каракули», чтобы никакие две гласные не стояли рядом;

6. «группоид», чтобы не менялся порядок гласных букв;

7. «перемена», чтобы три буквы «е» не шли подряд;

8. «столовая», чтобы никакие две гласные не стояли рядом;

9. «фигура», чтобы согласные шли в алфавитном порядке;

10. «баобаб», чтобы три буквы «б» не шли подряд;

11. «тетрадь», чтобы «ь» шла непосредственно после «р»;

12. «колокола», чтобы две буквы «о» не шли подряд;

13. «симфония», чтобы никакие две согласные не стояли рядом;

14. «симметрия», чтобы не менялся порядок гласных букв;

15. «кукуруза», чтобы две буквы «у» не шли подряд;

16. «алгебра», чтобы «р» шла непосредственно после «а»;

17. «автобус», чтобы гласные шли в алфавитном порядке;

18. «карандаш», чтобы две буквы «а» не шли подряд;

19. «решение», чтобы «е» шла непосредственно после «н»;

20. «множество», чтобы согласные шли в алфавитном порядке;

21. «апелляция», чтобы «я» шла непосредственно после «л»;

22. «гиппопотам», чтобы гласные шли в алфавитном порядке;

23. «баллада», чтобы две буквы «а» не шли подряд;

24. «интеллект», чтобы «л» шла непосредственно после «е»;

25. «идиллия», чтобы три буквы «и» не шли подряд;

26. «пассажир», чтобы согласные шли в алфавитном порядке;

27. «диаграмма», чтобы «м» шла непосредственно после «а»;

28. «оперетта», чтобы не менялся порядок гласных букв;

29. «гипербола», чтобы гласные шли в алфавитном порядке;

30. «баррикада», чтобы две буквы «а» не шли подряд;

31. «программа», чтобы «а» шла непосредственно после «р»;

32. «кенгуру», чтобы согласные шли в алфавитном порядке;

33. «колоннада», чтобы «о» шла непосредственно после «к»;

34. «килограмм», чтобы гласные шли в алфавитном порядке;

35. «бестселлер», чтобы две буквы «е» не шли подряд;

36. «периметр», чтобы «е» шла непосредственно после «р»;

37. «поговорка», чтобы согласные шли в алфавитном порядке;

38. «междометие», чтобы «м» шла непосредственно после «е»;

39. «профессор», чтобы не менялся порядок гласных букв;

40. «корректор», чтобы три буквы «р» не шли подряд.

Литература

1. Алексеев В. Е. Элементы комбинаторики. – Пособие для студентов заочного отделения, Нижний Новгород, 2001.

2. Алексеев В.Е., Киселева Л.Г., Смирнова Т.Г. Задачи по дискретной математике. – Методическая разработка, Нижний Новгород, 2003.

3. Виленкин Н. Я. Комбинаторика. – М.: Наука, 1969.

4. Гаврилов Г.Н., Сапоженко А.А. Сборник задач по дискретной математике. – М.: Наука, 1977.

5. Ежов И.И., Скороход А.В., Ядренко М.И. Элементы комбинаторики. – М.: Наука, 1977.

6. Киселева Л.Г. Элементы комбинаторики. – Методическая разработка, Нижний Новгород, 1990.

7. Киселева Л.Г., Смирнова Т.Г. Тождества и уравнения в алгебре множеств. – Методическая разработка, Нижний Новгород, 1999.

8. Марков А.А. Элементы комбинаторного анализа. – Методическая разработка, Горький, 1988.

9. Яблонский С.В. Введение в дискретную математику. М.: Наука, 1986.

СОДЕРЖАНИЕ

§1. Сочетания, размещения, перестановки 3

§2. Основные правила комбинаторики 4

§3. Число сочетаний, размещений и размещений с повторениями 8

§4. Основные свойства биномиальных коэффициентов 11

§5. Бином Ньютона 12

§6. Разбиение множества 13

§7. Перестановки с фиксированным числом повторений 16

§8. Число сочетаний с повторениями 21

§9. Формула включений и исключений 22

Задачи 24

Контрольные задания 32

Литература 39