N - список или множество объектов или целое число

Лабораторная работа № 4.

Комбинаторика.

Цель работы: Решение комбинаторных задач с использованием программы
Maple.
В программе Mapleимеется специальный пакет функций – combinat,которыйпозволяет решать комбинаторные задачи.
Пакет функций вызывается следующим образом:
> with(combinat):

Рассмотрим некоторые функции пакета combinatи напомним применение оператора -- $.

$ - оператор для формирования последовательности выражений

Синтаксис
expr $ i = m..n
expr $ n -- сокращенная форма: expr $ i = 1.. n( когдаexpr
не содержит i)
$m..n -- сокращенная форма: i $ i = m..n

Параметры
expr – выражение
i – имя
m,n - выражения

Описание
Вы можете использовать оператор$, чтобы сформировать последовательность выражений (перечисленных через запятую выражений -- expr, вычисленных, подстановкой вместоi вexprзначения m, m+1,..., n ).
Еслиm> n тогдаПУСТАЯ последовательность выражения возвращена.
Обратите внимание: Это рекомендует (и часто необходимо), что и'expr' и'i' взяты в апострофы, самое общее использование -'expr' $'i' = м.. n;
Примеры
> $ 2..5;

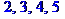
> i^2 $i=2/3..8/3;

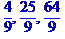
> a[i]$ i=1..4;

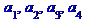
> x$4;

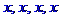
> '$1..5'$3;

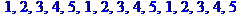
> EX:='x+k' $ 'k'=2..3;

> x:=2:
> EX;

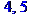
Функция combinat [choose] - возвращает неупорядоченные выборки списка.

Синтаксис обращения к функции:

Choose(n)

Choose(n, m)

Параметры:

N - список или множество объектов или целое число

M - (дополнительное) целое число

Описание:

Если n -- список/множество, тогда choose возвращает список/множество из элементов которые являются всевозможными неупорядоченными выборками из n по m без повторений . Если n - неотрицательное целое число, то это интерпретируется так, как список первых n целых чисел.

Если m задается, то только выборки размера m возвращены; иначе, выборки всех размеров возвращены, включая пустую комбинацию. Обратите внимание, что дубликаты в списке n приняты как различные элементы.

Команда with(combinat,choose), позволяет использование сокращенной формы этой команды.

Примеры:

> with(combinat):

Чтобы получить список сочетаний без повторений из n=3 элементов по m=2:

> choose([1,2,3],2);

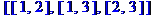
Или тоже самое

> choose(3,2);

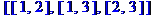
Чтобы получить список сочетаний с повторениями из n=3 элементов по m=2,необходимо в списке n каждый элемент повторить m раз:

> choose([1,1,2,2,3,3],2);

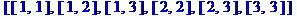
Или тоже самое

> choose([1$2,2$2,3$2],2);

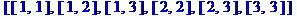
или тоже самое:

> choose(['$1..3' $ 2],2);

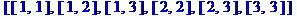
Функция numbcomb(n,m) -- возвращает число неупорядоченных выборок из n по m.

Например:

> numbcomb(3,2);

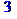
> numbcomb([1$2,2$2,3$2],2;

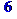
или тоже самое:

> numbcomb(['$1..3' $ 2],2);

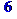
Функция binomial (n, r) — возвращает биноминальные коэффициенты, причем, если n и r — целые числа, удовлетворяющие условию 0 <= r<= n, то функция возвращает C(n.r)=n!/(r!(n-r)!)
Пример:
> binomial(4, 2);

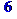
Функция partition(n,m) — возвращает список всех возможных сумм, дающих n.

Синтактис обращения к функции:

Partition(n)

Partition(n,m)

Параметры:

N - целое положительное число

Permute(n)

permute(n, r)

Параметры:

N - список/множество объектов или целое число

Лабораторная работа № 4.

Комбинаторика.

Цель работы: Решение комбинаторных задач с использованием программы
Maple.
В программе Mapleимеется специальный пакет функций – combinat,которыйпозволяет решать комбинаторные задачи.
Пакет функций вызывается следующим образом:
> with(combinat):

Рассмотрим некоторые функции пакета combinatи напомним применение оператора -- $.

$ - оператор для формирования последовательности выражений

Синтаксис
expr $ i = m..n
expr $ n -- сокращенная форма: expr $ i = 1.. n( когдаexpr
не содержит i)
$m..n -- сокращенная форма: i $ i = m..n

Параметры
expr – выражение
i – имя
m,n - выражения

Описание
Вы можете использовать оператор$, чтобы сформировать последовательность выражений (перечисленных через запятую выражений -- expr, вычисленных, подстановкой вместоi вexprзначения m, m+1,..., n ).
Еслиm> n тогдаПУСТАЯ последовательность выражения возвращена.
Обратите внимание: Это рекомендует (и часто необходимо), что и'expr' и'i' взяты в апострофы, самое общее использование -'expr' $'i' = м.. n;
Примеры
> $ 2..5;

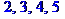
> i^2 $i=2/3..8/3;

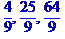
> a[i]$ i=1..4;

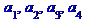
> x$4;

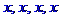
> '$1..5'$3;

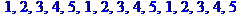
> EX:='x+k' $ 'k'=2..3;

> x:=2:
> EX;

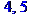
Функция combinat [choose] - возвращает неупорядоченные выборки списка.

Синтаксис обращения к функции:

Choose(n)

Choose(n, m)

Параметры:

n - список или множество объектов или целое число