Нечеткая и лингвистическая переменные

Нечеткая переменная определяется кортежем 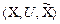, где X — наименование нечеткой переменной; 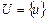— область ее определения, или универсальное множество; 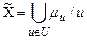— нечеткое множество на U, описывающее ограничение на возможные числовые значения нечеткой переменной X.

Лингвистическая переменная определяется кортежем

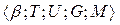, (1.7)

где β – наименование лингвистической переменной; Т – множество ее значений, или термов, представляющих собой наименования нечетких переменных, областью определения каждой из которых является множество U. Например, для лингвистической переменной, представленной на рис. 1.3, 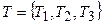, , 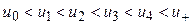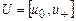. Пару точек 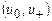будем называть граничной парой. В дальнейшем без особой необходимости не будем различать переменную и ее наименование.

Множество Т будем называть базовым терм-множеством лингвистической переменной; G — синтаксическая процедура, описывающая процесс образования из множества Т новых, осмысленных для данной задачи ПР значений лингвистической переменной. Множество 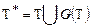назовем расширенным терм-множеством лингвистической переменной; М — семантическая процедура, позволяющая приписать каждому новому значению, образуемому процедурой G, некоторую семантику путем формирования соответствующего нечеткого множества, т. е. отобразить новое значение в нечеткую переменную.

Рассмотрим пример лингвистической переменной. Пусть ЛПР оценивает посадочную скорость летательных аппаратов с помощью понятий «малая», «небольшая», «средняя», «высокая». При этом максимальная посадочная скорость равна 300 км/ч. Формализация такого описания может быть проведена с помощью лингвистической переменной <СКОРОСТЬ, {МАЛАЯ, НЕБОЛЬШАЯ, СРЕДНЯЯ, ВЫСОКАЯ}, [0, 300], G, М>, где G — процедура перебора элементов базового терм-множества, М — процедура экспертного опроса.

В общем случае взаимосвязь лингвистической и нечеткой переменных графически может быть представлена как показано на рисунке 2. Здесь Т={Т₁, Т₂, Т₃, Т₄}, u₀< u₂ < u₁ < u₄ < u₃ < u₆ < u₅ <u₇, U = [u₀, u₇]. Пара точек (u₀, u₁) называется граничной парой.

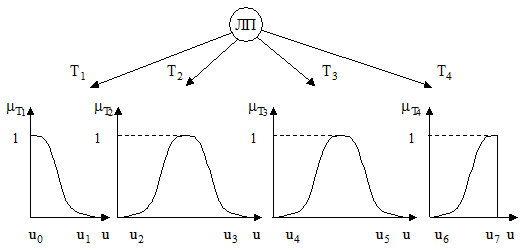
Рисунок 2. – Взаимосвязь лингвистической и нечеткой переменных

Нечеткие числа и функции.

В зависимости от характера множества U лингвистические переменные могут быть разделены на числовые и нечисловые. Числовой называется лингвистическая переменная, у которой 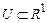, где 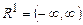, и которая имеет измеримую базовую переменную.

Нечеткие переменные, соответствующие значениям числовой лингвистической переменной, будем называть нечеткими числами. Если 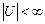, то нечеткие числа будем считать дискретными, если же 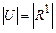— то непрерывными. Приведенная выше лингвистическая переменная СКОРОСТЬ является числовой, а нечеткие переменные из ее терм-множества — непрерывными нечеткими числами.

Примером нечисловой лингвистической переменной может служить переменная СЛОЖНОСТЬ, формализующая понятие «сложность разработки», со значениями НИЗКАЯ, СРЕДНЯЯ, УМЕРЕННАЯ, ВЫСОКАЯ.

К функциям принадлежности нечетких чисел обычно предъявляется ряд требований, которые обсуждаются в § 3.1, 3.2.

Пусть 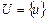, 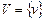— два универсальных множества; 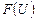— система всех нечетких множеств, заданных на U. Используяданные обозначения, определяем три типа функций:

четкая функция нечеткого аргумента

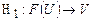, (1.8)

нечеткая функция четкого аргумента

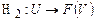, (1.9)

нечеткая функция нечеткого аргумента

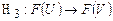, (1.10)

Использование основных понятий лингвистического подхода — лингвистической переменной и нечеткого множества — с целью формализации нечетких описаний элементов задач ПР, а именно критериев, предпочтений ЛПР, случайных исходов, качественных зависимостей между параметрами альтернатив и оценками исходов, приводит к необходимости рассмотрения лингвистических критериев и отношений предпочтения, лингвистических вероятностей, нечетких свидетельств.

1.5. НЕЧЕТКИЕ ВЫСКАЗЫВАНИЯ. ПРАВИЛА

ПРЕОБРАЗОВАНИЯ НЕЧЕТКИХ ВЫСКАЗЫВАНИЙ

Нечеткими высказываниями [19] назовем высказывания следующего вида:

1) высказывание <b есть a>, где b — наименование лингвистической переменной, отражающей некоторый объект или параметр реальной действительности, относительно которой производится утверждение a, являющееся ее нечеткой оценкой (нечеткой переменной). Например, (давление большое). В высказывании <толщина равна 14 мм> значение a = 14 мм является четкой оценкой лингвистической переменной b: <толщина>;

2) высказывания вида <b есть ma> , <b есть Qa>, <Qb есть ma>,<mb есть Qa>, при этом m называется модификатором (ему соответствуют такие слова, как ОЧЕНЬ, БОЛЕЕ ИЛИ МЕНЕЕ, НЕЗНАЧИТЕЛЬНЫЙ, СРЕД­НИЙ и др.), Q - квантификатором (ему соответствуют слова типа БОЛЬШИНСТВО, НЕСКОЛЬКО, МНОГО, НЕМНОГО, ОЧЕНЬ МНОГО и др.). Например, <давление очень большое>, <большинство значений параметра очень мало>;

3) высказывания, образованные из высказываний 1-го и 2-го видов и союзов И; ИЛИ; ЕСЛИ. . ., ТО. . .; ЕСЛИ. . ., ТО . . . ИНАЧЕ. Напри­мер, <ЕСЛИ давление большое, ТО толщина не мала>.

Необходимо отметить, что отождествление данных союзов с логичес­кими операциями конъюнкций, дизъюнкций, отрицанием и импликаци­ей возможно только при предварительном рассмотрении опроса комму­тативности, ассоциативности и дистрибутивности высказываний, образу­ющих предложения.

Предположим, имеются некоторые высказывания C̃ и D̃ относительно ситуации A. Пусть рассматриваемые высказывания имеют вид C̃: <b есть a_C> и D̃: <b есть a_D>, где a_C и a_D - нечеткие переменные, определен­ные на универсальном множестве U = {u}

Определение 1.15 Истинность высказывания C̃ и D̃ относительно C̃ есть значение функции T(D̃ / C̃), определяемое степенью соответствия высказываний C̃ и D̃̃̃ . В формальной записи

T (D̃/C̃) = {< μ_T(t) /t},

где

("u Î U) (t = μ_D̃(u));

μ_T(t) = max μ_C̃(u), U^/ = {u Î U| μ_D(u) = t }, u Î U^/

при этом μ_D̃ и μ_С̃ – функции принадлежности нечётких переменных a_С̃ a_D; μ_T(t) – функция принадлежности значения истинности; t Î [0,1] – область её определения.

Иными словами, истинностью, нечеткого высказывания D относительно нечеткого высказывания С является нечеткое множество T(D/C),определенное на интервале [0,1], такое, что для любого tÎ[0,1] значение ее функции принадлежности равно наибольшему значению μ_C̃(u) по всем u, при которых μ_D̃(u) = t.

Пример 1.11. Предположим, что сформулировано высказывание D:<b находится близко к 5>, в то время как С: <b имеет значение при­близительно 6>. Пусть a_D̃ есть "близко к 5", a_C есть "приблизительно 6" суть нечеткие переменные с нечеткими множествами:

C_C̃ = {<0,1/2>, <0,3/3>, <0,7/4>, <1/5>,

<0,8/6>, <0,6/7>, <0,3/8>, <0,1/9>,

<0,8/6>, <0,6/7>, <0,3/8>, <0,1/9> };

C_D̃ = {<0,1/3>, <0,4/4>, <0,8/5>, <1/6>,

<0,7/7>, <0,4/8>, <0,3/9>, <0,1/10>}.

В этом случае U= { 2, 3_4, 5, 6, 7, 8, 9, 10 } . Тогда истинность высказывания D относительно С будет иметь следующий вид:

Т(D̃/C̃) = {<0,1/0>, <0,3/0,1>, <0,4/0,3>,

<0,7/0,6>, <0,4/0,7>, <1/0,8>, <0,8/1>}.