Какие виды неопределенности выделяют.

Введение

Наиболее поразительным свойством человеческого интеллекта яв­ляется способность принимать правильные решения в обстановке неполной и нечеткой информации. Построение моделей приближенных рассуждений человека и использование их в компьютерных системах будущих поколений представляет сегодня одну из важнейших проблем науки.

При изучении сложных систем, где человек играет существенную роль, действует так называемый принцип несовместимости [1]: для получения существенных выводов о поведении сложной системы необходимо отказаться от высоких стандартов точности и строгости, которые характерны для сравнительно простых систем, и привлекать к ее анализу подходы, которые являются приближенными по своей природе.

При попытке формализовать человеческие знания исследователи столкнулись с проблемой, затруднявшей использование традиционного математиче­ского аппарата для их описания. Существует целый класс описаний, оперирую­щих качественными характеристиками объектов (много, мало, сильный, очень и т. п.) Эти характеристики обычно размыты и не могут быть однознач­но интерпретированы, однако содержат важную информацию (например, «Од­ним из возможных признаков гриппа является высокая температура»).

Категория нечеткости и связанные с ней модели и методы очень важны с мировоззренческой точки зрения, поскольку с их появлением стало возможно подвергать количественному анализу те явления, которые раньше либо могли быть учтены только на качественном уровне, либо требовали использования весьма грубых моделей.

Значительное продвижение в этом направлении сделано примерно 35 лет тому назад профессором Калифорнийского университета (Беркли) Лотфи А. Заде (Lotfi A. Zadeh). Его работы легли в основу моделирования интеллектуальной деятельности человека и явились начальным толчком к развитию новой математической теории.

Что же предложил Заде? Во-первых, он расширил классическое понятие множества, допустив, что характеристическая функция (функция принадлежности элемента множеству) может принимать любые значения в интервале (0;1), а не только значения 0 либо 1. Такие множества были названы им нечеткими (fuzzy). Л.Заде определил также ряд операций над нечеткими множествами и предложил обобщение известных методов логического вывода modus ponens и modus tollens.

Введя затем, понятие лингвистической переменной и допустив, что в качестве ее значений (термов) выступают нечеткие множества, Л.Заде создал аппарат для описания процессов интеллектуальной деятельности, включая нечеткость и неопределенность выражений.

Вот точка зрения Л.Заде: "Я считаю, что излишнее стремление к точности стало оказывать действие, сводящее на нет теорию управления и теорию систем, так как оно приводит к тому, что исследования в этой области сосредоточиваются на тех и только тех проблемах, которые поддаются точному решению. В результате многие классы важных проблем, в которых данные, цели и ограничения являются слишком сложными или плохо определенными для того, чтобы допустить точный математический анализ, оставались и остаются в стороне по той причине, что они не поддаются математической трактовке. Для того чтобы сказать что-либо существенное для проблем подобного рода, мы должны отказаться от наших требований точности и допустить результаты, которые являются несколько размытыми или неопределенными".

Математическая теория нечетких множеств позволяет описывать нечеткие понятия и знания, оперировать этими знаниями и делать нечеткие выводы. Основанные на этой теории методы построения компьютерных нечетких систем существенно расширяют области применения компьютеров.

Нечеткая Логика - в основном многозадачная логика, которая позволяет определять промежуточные значения между стандартными оценками подобно Да/Нет, Истина/Ложь, Черное/Белое, и т.д. Понятия подобно "довольно теплый" или "довольно холодный" могут быть сформулированы математически и обработаны компьютерами. Таким образом, сделана попытка применить человекоподобное мышление в программировании компьютера.

В последнее время нечеткое управление является одной из самых активных и результативных областей исследований применения теории нечетких множеств. Нечеткое управление оказывается особенно полезным, когда технологические процессы являются слишком сложными для анализа с помощью общепринятых количественных методов, или когда доступные источники информации интерпретируются качественно, неточно или неопределенно. Экспериментально показано, что нечеткое управление дает лучшие результаты, по сравнению с результатами, получаемыми при общепринятых алгоритмах управления. Нечеткие методы помогают управлять домной и прокатным станом, автомобилем и поездом, распознавать речь и изображения, проектировать роботов, обладающих осязанием и зрением. Нечеткая логика, на которой основано нечеткое управление, ближе по духу к человеческому мышлению и естественным языкам, чем традиционные логические системы. Нечеткая логика обеспечивает эффективные средства отображения неопределенностей и неточностей реального мира. Наличие математических средств отражения нечеткости исходной информации позволяет построить модель, адекватную реальности.

Применение нечеткой логики

Применение нечеткого управления эффективно ...

· Для очень сложных процессов, когда имеется сложная математическая модель

· Для нелинейных процессов

· Если должна выполняться обработка экспертных знаний

Применение нечеткого управления не имеет смысла, если ...

· Стандартная теория управления дает удовлетворяющий результат

· Легко разрешимая и адекватная математическая модель уже существует

· Проблема не разрешима

Нечеткие числа и функции.

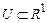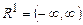В зависимости от характера множества U лингвистические переменные могут быть разделены на числовые и нечисловые. Числовой называется лингвистическая переменная, у которой , где , и которая имеет измеримую базовую переменную.

Нечеткие переменные, соответствующие значениям числовой лингвистической переменной, будем называть нечеткими числами. Если 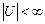, то нечеткие числа будем считать дискретными, если же 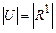— то непрерывными. Приведенная выше лингвистическая переменная СКОРОСТЬ является числовой, а нечеткие переменные из ее терм-множества — непрерывными нечеткими числами.

Примером нечисловой лингвистической переменной может служить переменная СЛОЖНОСТЬ, формализующая понятие «сложность разработки», со значениями НИЗКАЯ, СРЕДНЯЯ, УМЕРЕННАЯ, ВЫСОКАЯ.

К функциям принадлежности нечетких чисел обычно предъявляется ряд требований, которые обсуждаются в § 3.1, 3.2.

Пусть 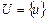, 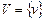— два универсальных множества; 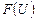— система всех нечетких множеств, заданных на U. Используяданные обозначения, определяем три типа функций:

четкая функция нечеткого аргумента

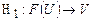, (1.8)

нечеткая функция четкого аргумента

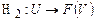, (1.9)

нечеткая функция нечеткого аргумента

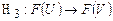, (1.10)

Использование основных понятий лингвистического подхода — лингвистической переменной и нечеткого множества — с целью формализации нечетких описаний элементов задач ПР, а именно критериев, предпочтений ЛПР, случайных исходов, качественных зависимостей между параметрами альтернатив и оценками исходов, приводит к необходимости рассмотрения лингвистических критериев и отношений предпочтения, лингвистических вероятностей, нечетких свидетельств.

1.5. НЕЧЕТКИЕ ВЫСКАЗЫВАНИЯ. ПРАВИЛА

ПРЕОБРАЗОВАНИЯ НЕЧЕТКИХ ВЫСКАЗЫВАНИЙ

Нечеткими высказываниями [19] назовем высказывания следующего вида:

1) высказывание <b есть a>, где b — наименование лингвистической переменной, отражающей некоторый объект или параметр реальной действительности, относительно которой производится утверждение a, являющееся ее нечеткой оценкой (нечеткой переменной). Например, (давление большое). В высказывании <толщина равна 14 мм> значение a = 14 мм является четкой оценкой лингвистической переменной b: <толщина>;

2) высказывания вида <b есть ma> , <b есть Qa>, <Qb есть ma>,<mb есть Qa>, при этом m называется модификатором (ему соответствуют такие слова, как ОЧЕНЬ, БОЛЕЕ ИЛИ МЕНЕЕ, НЕЗНАЧИТЕЛЬНЫЙ, СРЕД­НИЙ и др.), Q - квантификатором (ему соответствуют слова типа БОЛЬШИНСТВО, НЕСКОЛЬКО, МНОГО, НЕМНОГО, ОЧЕНЬ МНОГО и др.). Например, <давление очень большое>, <большинство значений параметра очень мало>;

3) высказывания, образованные из высказываний 1-го и 2-го видов и союзов И; ИЛИ; ЕСЛИ. . ., ТО. . .; ЕСЛИ. . ., ТО . . . ИНАЧЕ. Напри­мер, <ЕСЛИ давление большое, ТО толщина не мала>.

Необходимо отметить, что отождествление данных союзов с логичес­кими операциями конъюнкций, дизъюнкций, отрицанием и импликаци­ей возможно только при предварительном рассмотрении опроса комму­тативности, ассоциативности и дистрибутивности высказываний, образу­ющих предложения.

Предположим, имеются некоторые высказывания C̃ и D̃ относительно ситуации A. Пусть рассматриваемые высказывания имеют вид C̃: <b есть a_C> и D̃: <b есть a_D>, где a_C и a_D - нечеткие переменные, определен­ные на универсальном множестве U = {u}

Определение 1.15 Истинность высказывания C̃ и D̃ относительно C̃ есть значение функции T(D̃ / C̃), определяемое степенью соответствия высказываний C̃ и D̃̃̃ . В формальной записи

T (D̃/C̃) = {< μ_T(t) /t},

где

("u Î U) (t = μ_D̃(u));

μ_T(t) = max μ_C̃(u), U^/ = {u Î U| μ_D(u) = t }, u Î U^/

при этом μ_D̃ и μ_С̃ – функции принадлежности нечётких переменных a_С̃ a_D; μ_T(t) – функция принадлежности значения истинности; t Î [0,1] – область её определения.

Иными словами, истинностью, нечеткого высказывания D относительно нечеткого высказывания С является нечеткое множество T(D/C),определенное на интервале [0,1], такое, что для любого tÎ[0,1] значение ее функции принадлежности равно наибольшему значению μ_C̃(u) по всем u, при которых μ_D̃(u) = t.

Пример 1.11. Предположим, что сформулировано высказывание D:<b находится близко к 5>, в то время как С: <b имеет значение при­близительно 6>. Пусть a_D̃ есть "близко к 5", a_C есть "приблизительно 6" суть нечеткие переменные с нечеткими множествами:

C_C̃ = {<0,1/2>, <0,3/3>, <0,7/4>, <1/5>,

<0,8/6>, <0,6/7>, <0,3/8>, <0,1/9>,

<0,8/6>, <0,6/7>, <0,3/8>, <0,1/9> };

C_D̃ = {<0,1/3>, <0,4/4>, <0,8/5>, <1/6>,

<0,7/7>, <0,4/8>, <0,3/9>, <0,1/10>}.

В этом случае U= { 2, 3_4, 5, 6, 7, 8, 9, 10 } . Тогда истинность высказывания D относительно С будет иметь следующий вид:

Т(D̃/C̃) = {<0,1/0>, <0,3/0,1>, <0,4/0,3>,

<0,7/0,6>, <0,4/0,7>, <1/0,8>, <0,8/1>}.

Рисунок 11 – Значения аргумента, Рисунок 12 – Значения аргумента,

Значение 0,5 значение 0,25

· назначьте значение аргумента, для которого значение ФП (0,75) лежит посередине между значениями ФП для точек 0,0 и 0,35.

Предположим, что это будет значение аргумента равное 0,12 (рисунок 13).

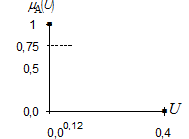
Рисунок 13 – Значения аргумента, при котором ФП принимает значение 0,75

Таким образом, результаты выполнения предыдущих действий для данного терма будут такими:

Значения аргумента	0,0	0,12	0,35	0,38	0,40
Степени принадлежности	1,0	0,75	0,50	0,25	0,0

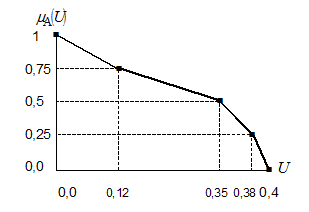
Рисунок 14 – Графическое изображение результатов

для терма "Вероятность малая"

7.2Рассмотрим 2 терм и определим семантику терма "Вероятность средняя". Для него определим значения ФП в граничных точках. В этом случае значения ФП равны 0, так как и меньше Р < 0,2 и при Р > 0,8 вероятность не может считаться средней.

Граничные значения 0,2 0,8

Значения ФП 0 0

Графически решение этой задачи показано на рисунке 15.

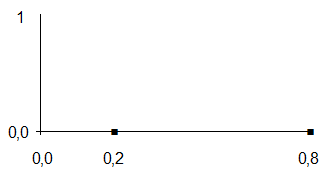
Рисунок 15 – Значения ФП в граничных точках

для терма "Вероятность средняя"

Нахождение значений ФП в данном интервале.

Для простоты воспользуемся 3-х кратным разбиением. Методика разбиения состоит в следующем:

· назначьте значение аргумента, при котором ФП уже равна 1, и значение аргумента, при котором она еще равна 1.

Предположим, это будут значения аргумента равные 0,3 и 0,7 (рисунок 16).

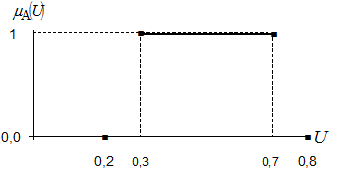
Рисунок 16 – Значения аргумента, при котором ФП принимает значение 1,0.

· назначьте значение аргумента, для которого значение ФП (0,5) лежит посередине между значениями ФП для точек 0,2 и 0,3.

Предположим, что это будет значение аргумента равное 0,27.

· назначьте значение аргумента, для которого значение ФП (0,75) лежит посередине между значениями ФП для точек 0,27 и 0,3.

Предположим, что это будет значение аргумента равное 0,282.

· назначьте значение аргумента, для которого значение ФП (0,25) лежит посередине между значениями ФП для точек 0,2 и 0,27.

Предположим, что это будет значение аргумента равное 0,24.

Рассмотрим правый полуинтервал для терма "Вероятность средняя".

· назначьте значение аргумента, для которого значение ФП (0,5) лежит посередине между значениями ФП для точек 0,7 и 0,8.

Предположим, что это будет значение аргумента равное 0,74.

· назначьте значение аргумента, для которого значение ФП (0,75) лежит посередине между значениями ФП для точек 0,7 и 0,74.

Предположим, что это будет значение аргумента равное 0,72.

· назначьте значение аргумента, для которого значение ФП (0,25) лежит посередине между значениями ФП для точек 0,74 и 0,8.

Предположим, что это будет значение аргумента равное 0,76.

Таким образом, результаты выполнения предыдущих действий для терма "Вероятность средняя" будут такими:

Значения аргумента	0,2	0,24	0,27	0,282	0,3	0,7	0,72	0,74	0,76	0,8
Степени принадлежности	0,0	0,250	0,500	0,750	1,0	1,0	0,75	0,5	0,25

Графически это решение показано на рисунке 17.

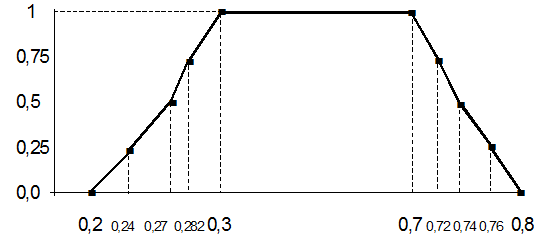
Рисунок 17 – Вид ФП для терма "Вероятность средняя"

7.3Рассмотрим 3 терм и определим семантику терма "Вероятность большая". Для него определим значения ФП в граничных точках.

Граничные значения	0,600	1,0
Значения ФП

Графически решение этой задачи показано на рисунке 18.

Нахождение значений ФП в данном интервале.

Методика выполнения данного этапа аналогична 7.1, поэтому представим только конечные результаты.

· значение аргумента, для которого значение ФП (0,5) лежит посередине между значениями ФП для точек 0,6 и 1,0 равно 0,7.

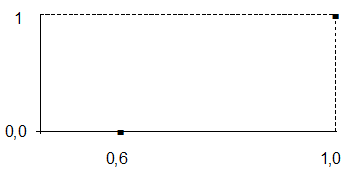
Рисунок 18 – Значения ФП в граничных точках

для терма "Вероятность большая"

· значение аргумента, для которого значение ФП (0,25) лежит посередине между значениями ФП для точек 0,6 и 0,7 равно 0,64.

· значение аргумента, для которого значение ФП (0,75) лежит посередине между значениями ФП для точек 0,7 и 1,0 равно 0,85.

Таким образом, результаты выполнения расчетов для данного терма будут такими:

Значения аргумента	0,6	0,64	0,7	0,85	1,0
Степени принадлежности	0,0	0,250	0,500	0,750	1,0

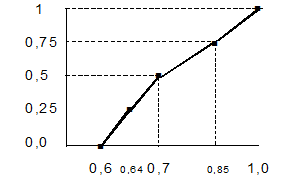
Рисунок 19 – Вид ФП для терма "Вероятность большая"

Вывод. Таким образом, в результате выполнения всех этапов можно построить функцию принадлежности лингвистической переменной "Вероятность" (рисунок 12).

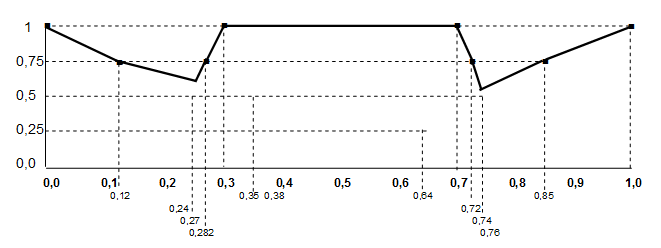
Рисунок 20 – Общий вид функции принадлежности лингвистической

переменной "Вероятность"

КОСВЕННЫЙ МЕТОД ПОСТРОЕНИЯ ФП

Одним из возможных методов построения функции принадлежности является метод, основанный на количественном сравнении степеней принадлежности индивидуальным ЛПР (лицо, принимающее решение). Результатом опроса ЛПР является матрица 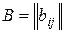размера n´n, где n – число точек 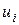, в которых сравниваются значения функции принадлежности. Элемент 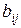матрицы В является субъективной оценкой отношения 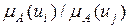и показывает, во сколько раз, по мнению ЛПР, 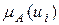больше 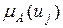. Величина назначается в соответствии с балльной шкалой, значения которой интерпретируются в соответствии со шкалой интенсивности.

По определению 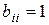и с целью согласования оценок ЛПР устанавливается, что 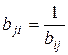. Значения функции принадлежности 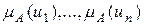в точках 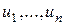определяются на основе решения задачи о нахождении собственного вектора матрицы В

,

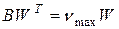где 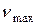– максимальное собственное число матрицы В; 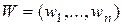– соответствующий собственный вектор; ^т – символ транспонирования.

Поскольку матрица В является положительной по построению, решение этой задачи всегда существует и является единственным. Можно показать, что в этом случае

.

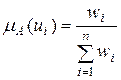При этом значения функции принадлежности 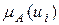оказываются измеренными в шкале отношений. Описанный метод обладает рядом достоинств:

- применяемая в методе процедура парных сравнений является достаточно простой для ЛПР, поскольку она не навязывает ему априорных ограничений, например не требует транзитивности суждений;

- метод допускает наблюдаемую на практике несогласованность оценок эксперта (имеется в виду, что 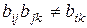) и вместе с тем позволяет учесть и оценить ее введением коэффициента несогласованности. Если 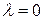, то наблюдается ситуации полной согласованности суждений; чем больше l, тем больше несогласованность суждений ЛПР;

- решение задачи о собственном векторе приводит к измерению функции принадлежности в шкале отношений.

МОДЕЛЬНЫЙ ПРИМЕР

Для иллюстрации этапов получения решения задачи с помощью метода анализа иерархий рассмотрим гипотетический пример. Для уборки зерновых культур необходимо приобрести зерноуборочный комбайн. На рынке имеются машины нескольких фирм одинакового целевого назначения. Какой зернокомбайн выбрать в соответствии с потребностями покупателя? Другими словами необходимо оценить весомость критериев к машине, которыми пользуется потребитель.

Рекомендуется такая последовательность этапов при решении задачи.

1. Очертите проблему и определите, что вы хотите узнать.

2. Постройте иерархию, начиная с вершины (цели - с точки зрения управления), через промежуточные уровни (критерии, по которым зависят последующие уровни) к самому нижнему уровню (который обычно является перечнем альтернатив).

3. Постройте матрицу попарных сравнений для второго уровня.

4. Проверить согласованность, используя отклонение 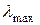от n.

Схема иерархии для рассматриваемой задачи приведена на рисунке. На первом (высшем) уровне находится общая цель: "Зернокомбайн". На втором уровне находятся показатели (критерии), уточняющие цель.

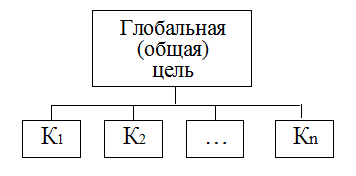
Рисунок 21 – Схема иерархии для решения проблемы выбора зернокомбайна

Примечание 1. В примере на втором уровне рассматриваются четыре критерия. Такое количество выбрано лишь для иллюстрации метода и не связано с сутью рассматриваемой проблемы – выбора лучшего зернокомбайна.

Примечание 2. Издавна известны магические свойства числа семь. Так вот в МАИ для проведения обоснованных численных сравнений не рекомендуется сравнивать более чем 7 ± 2 элементов. Если же возникает потребность в расширении уровней 2 и 3, то следует использовать принцип иерархической декомпозиции. Другими словами если число критериев, например, превышает десятки, то необходимо элементы сгруппировать в сравниваемые классы приблизительно из семи элементов в каждом.

После выполнения работ на этапе иерархического представления проблемы необходимо установить приоритеты критериев. Для количественного определения сравнительной важности факторов в проблемной ситуации необходимо составить матрицу попарных сравнений. Эта матрица представлена в таблице 1.

Таблица 1 – Общий вид матрицы попарных сравнений

Общее удовлетворение машиной	A1	A2	A3	. . .	AN
A1	1/1	w1/w2	w1/w3	. . .	w1/wn
A2	w2/w1	1/1	w2/w3	. . .	w2/wn
A3	w3/w1	w3/w2	1/1	. . .	w3/wn
. . .	. . .	. . .	. . .	1/1	. . .
AN	wn/w1	wn/w2	wn/w3	. . .	1/1

Здесь A₁, A₂, A₃, ..., A_n- множество из n элементов; w₁, w₂, w₃, ..., w_n- соответственно их веса или интенсивности.

Примечание 1. Цель составления подобной матрицы заключается в определении факторов с наибольшими величинами важности, чтобы затем сконцентрировать внимание на них при решении проблемы или разработке плана действий.

Примечание 2. Если ожидается, что w₁, w₂,..., w_n – неизвестны заранее (а это очень распространенная ситуация), то попарные сравнения элементов производятся с использованием субъективных суждений, численно оцениваемых по шкале (см. приложение).

Примечание 3. Следует подчеркнуть, что в МАИ по соглашению сравнивается относительная важность левых элементов матрицы с элементами наверху. Поэтому если элемент слева важнее, чем элемент наверху, то в клетку заносится положительное целое (от 1 до 9); в противном случае – обратное число (дробь, например, 1/5). Относительная важность любого элемента, сравниваемого с самим собой, равна 1; поэтому диагональ матрицы (таблица 1) содержит только единицы. Наконец, обратными величинами заполняют симметричные клетки, т.е. если элемент А₁ воспринимается как слегка более важный. (3 на шкале) относительно элемента А₂, то считается, что элемент А₂ слегка менее важен (1/3 по шкале) относительно элемента А₁.

Составим матрицу попарных сравнений для нашей задачи (таблица 2).

Таблица 2 – Матрица попарных сравнений, построенная

на основе субъективных суждений

Общее удовлетворение комбайном	Пр.	П.з.	Нар.	Р.т.	Ст.
Производительность	1/1	5/1	4/1	5/1	3/1
Потери зерна	1/5	1/1	1/2	2/1	1/2
Наработка	1/4	2/1	1/1	1/1	1/4
Расход топлива	1/5	1/2	1/1	1/1	1/2
Стоимость	1/3	2/1	4/1	2/1	1/1

Синтез приоритетов

Одним из способов определения приоритетов является вычисление геометрического среднего. Это можно сделать, перемножая элементы в каждой строке и извлекая корень n-й степени, где n – число элементов. Полученный таким образом столбец чисел нормализуется делением каждого числа на сумму всех чисел. Последовательность расчета составляющих вектора приоритетов приведена в таблице 3.

Таблица 3 – Расчет вектора приоритетов

	А1	А2	А3	А4	Оценки компонент собственного вектора по строкам	Нормализация результата
А1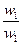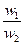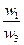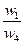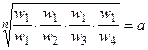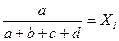
А2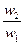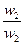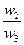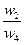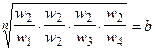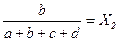
А3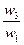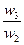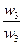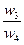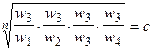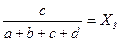
А4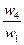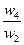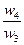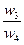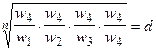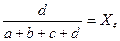

Для нашего примера значения вектора приоритетов (функции принадлежности) приведены в таблице 4.

Таблица 4 – Функция принадлежности

Общее удовлетворение комбайном	Вектор приоритетов, Xi
Производительность	0,491
Потери зерна	0,099
Наработка	0,104
Расход топлива	0,086
Стоимость	0,220

Приложение А

Введение

Наиболее поразительным свойством человеческого интеллекта яв­ляется способность принимать правильные решения в обстановке неполной и нечеткой информации. Построение моделей приближенных рассуждений человека и использование их в компьютерных системах будущих поколений представляет сегодня одну из важнейших проблем науки.

При изучении сложных систем, где человек играет существенную роль, действует так называемый принцип несовместимости [1]: для получения существенных выводов о поведении сложной системы необходимо отказаться от высоких стандартов точности и строгости, которые характерны для сравнительно простых систем, и привлекать к ее анализу подходы, которые являются приближенными по своей природе.

При попытке формализовать человеческие знания исследователи столкнулись с проблемой, затруднявшей использование традиционного математиче­ского аппарата для их описания. Существует целый класс описаний, оперирую­щих качественными характеристиками объектов (много, мало, сильный, очень и т. п.) Эти характеристики обычно размыты и не могут быть однознач­но интерпретированы, однако содержат важную информацию (например, «Од­ним из возможных признаков гриппа является высокая температура»).

Категория нечеткости и связанные с ней модели и методы очень важны с мировоззренческой точки зрения, поскольку с их появлением стало возможно подвергать количественному анализу те явления, которые раньше либо могли быть учтены только на качественном уровне, либо требовали использования весьма грубых моделей.

Значительное продвижение в этом направлении сделано примерно 35 лет тому назад профессором Калифорнийского университета (Беркли) Лотфи А. Заде (Lotfi A. Zadeh). Его работы легли в основу моделирования интеллектуальной деятельности человека и явились начальным толчком к развитию новой математической теории.

Что же предложил Заде? Во-первых, он расширил классическое понятие множества, допустив, что характеристическая функция (функция принадлежности элемента множеству) может принимать любые значения в интервале (0;1), а не только значения 0 либо 1. Такие множества были названы им нечеткими (fuzzy). Л.Заде определил также ряд операций над нечеткими множествами и предложил обобщение известных методов логического вывода modus ponens и modus tollens.

Введя затем, понятие лингвистической переменной и допустив, что в качестве ее значений (термов) выступают нечеткие множества, Л.Заде создал аппарат для описания процессов интеллектуальной деятельности, включая нечеткость и неопределенность выражений.

Вот точка зрения Л.Заде: "Я считаю, что излишнее стремление к точности стало оказывать действие, сводящее на нет теорию управления и теорию систем, так как оно приводит к тому, что исследования в этой области сосредоточиваются на тех и только тех проблемах, которые поддаются точному решению. В результате многие классы важных проблем, в которых данные, цели и ограничения являются слишком сложными или плохо определенными для того, чтобы допустить точный математический анализ, оставались и остаются в стороне по той причине, что они не поддаются математической трактовке. Для того чтобы сказать что-либо существенное для проблем подобного рода, мы должны отказаться от наших требований точности и допустить результаты, которые являются несколько размытыми или неопределенными".

Математическая теория нечетких множеств позволяет описывать нечеткие понятия и знания, оперировать этими знаниями и делать нечеткие выводы. Основанные на этой теории методы построения компьютерных нечетких систем существенно расширяют области применения компьютеров.

Нечеткая Логика - в основном многозадачная логика, которая позволяет определять промежуточные значения между стандартными оценками подобно Да/Нет, Истина/Ложь, Черное/Белое, и т.д. Понятия подобно "довольно теплый" или "довольно холодный" могут быть сформулированы математически и обработаны компьютерами. Таким образом, сделана попытка применить человекоподобное мышление в программировании компьютера.

В последнее время нечеткое управление является одной из самых активных и результативных областей исследований применения теории нечетких множеств. Нечеткое управление оказывается особенно полезным, когда технологические процессы являются слишком сложными для анализа с помощью общепринятых количественных методов, или когда доступные источники информации интерпретируются качественно, неточно или неопределенно. Экспериментально показано, что нечеткое управление дает лучшие результаты, по сравнению с результатами, получаемыми при общепринятых алгоритмах управления. Нечеткие методы помогают управлять домной и прокатным станом, автомобилем и поездом, распознавать речь и изображения, проектировать роботов, обладающих осязанием и зрением. Нечеткая логика, на которой основано нечеткое управление, ближе по духу к человеческому мышлению и естественным языкам, чем традиционные логические системы. Нечеткая логика обеспечивает эффективные средства отображения неопределенностей и неточностей реального мира. Наличие математических средств отражения нечеткости исходной информации позволяет построить модель, адекватную реальности.

Какие виды неопределенности выделяют.

1. Неопределенность, случайность:

1.1 события и (или) состояние среды, обусловленные случайностью;

1.2 явления, неподдающиеся анализу и измерению со сколь угодно большой точностью.

2. Нечеткость:

2.1 нечеткость как следствие субъективности или индивидуальности че­ловека;

2.2 нечеткость или неясность в процессах мышления и умозаключения:

2.2.1 – нечеткое или неточное заключение;

2.2.2 – неясность вследствие сложности и (или) многообразия выводов.

3. Нечеткость или неясность, сопутствующая естественным языкам:

3.1 нечеткость описания или представления;

3.2 неясность, связанная со сложностью и (или) многообразием семантик и структур естественных языков.

4. Расплывчатость или смутность рисунков, картин или сцен:

4.1 расплывчатость рисунков и картин;

4.2 неясность, возникающая в процессе интерпретации рисунков или картин.

5. Неясность вследствие структурной сложности и (или) многообразия информации

Применение нечеткой логики

Применение нечеткого управления эффективно ...

· Для очень сложных процессов, когда имеется сложная математическая модель

· Для нелинейных процессов

· Если должна выполняться обработка экспертных знаний

Применение нечеткого управления не имеет смысла, если ...

· Стандартная теория управления дает удовлетворяющий результат

· Легко разрешимая и адекватная математическая модель уже существует

· Проблема не разрешима