Формирование математической модели
Исходные данные
| (основные) | |
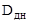 = 3,2 м | диаметр днища; |
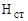 = 6780 мм | высота стенки; |
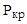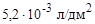 =  | расход красителя; |
| ПК = 1,4 кг/л | плотность краски; |
| (дополнительные) | |
| p = 3,1416 | число Пи; |
k1 = 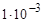 м/мм | коэффициент перевода мм в м; |
| k2 = 100 дм2/м2 | коэффициент перевода м2 в дм2. |
Расчетные зависимости
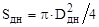 | [м2 = м2] | площадь днища, м2; |
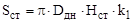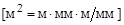 |  | площадь стенки, м2; |
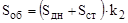 | [дм2 = (м2 +м2)×дм2/м2] | общая площадь, дм2; |
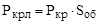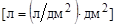 |  | расход краски, л; |
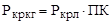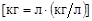 |  | расход краски, кг. |
Выбор метода решения
Анализ математической модели задачи позволяет сделать вывод, что реализация ее требует последовательного однократного выполнения всех математически сформулированных зависимостей, не содержащих нестандартных трансцендентных функций. Следовательно, в качестве метода решения необходим простой линейный вычислительный процесс.
Составление алгоритма решения
Для отработки методики структурирования, несмотря на относительную простоту математической модели и простейший метод решения, выполним схему алгоритма пошагово.
На первом шаге определим цель решения, на втором – выполним детализацию основных участков, на третьем – скомпонуем окончательный вариант алгоритма решения задачи (рис. 3.2). Конечный вариант алгоритма решения (шаг 3) предписывает естественный порядок его выполнения.
Естественный порядок выполнения алгоритма – однократная последовательная реализация всех указанных блоков, при которой номер каждого последующего на единицу больше предыдущего.
Программирование задачи
Составление программы решения требует предварительного ознакомления с элементами конкретного входного языка.
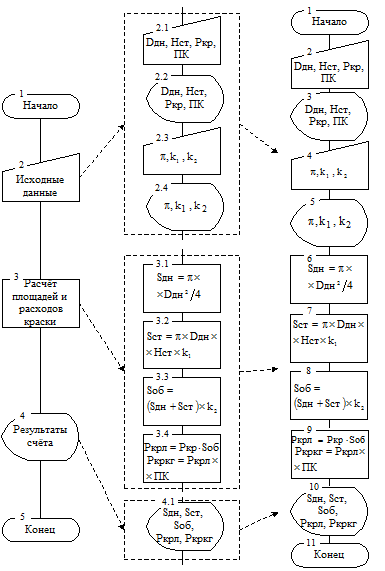
Шаг 1 Шаг 2 Шаг 3
Рис. 3.2. Структурированная схема алгоритма задачи 3.1
В качестве такого языка выбран универсальный язык программирования Си/Си++.
Первая версия языка программирования Си разработана и реализована в 1972 году сотрудником фирмы AT&T Bell Laboratories (США) Деннисом Ритчи. Растущая популярность языка Си обусловлена двумя причинами. Во-первых, Си – современный, эффективный, гибкий язык, который можно использовать для программирования прикладных задач. Во-вторых, он пригоден для создания системного программного обеспечения ЭВМ. На языке Си выполнены операционная система UNIX и система управления базами данных FoxPro.
За прошедшие десятилетия язык совершенствовался и дополнялся в рамках конкретных версий (Си, ТурбоСи).
В настоящее время наиболее распространена версия Си++. Все версии имеют общую базу и компонуются из стандартных элементов.
В предлагаемом издании излагается базовый компонент языков Си/Си++, ориентированный на программирование типовых задач начинающим пользователем.
Изложение основ языка Си/Си++ осуществляется по методике изучения разговорных языков – алфавит, простейшие, основные, сборные конструкции.
3.5.1. Алфавит Си/Си++
Алфавит языка программирования – совокупность букв, цифр и знаков (специальных символов), используемых в нем.
Алфавит языка Си/Си++ составляют 52 (заглавные и прописные) латинские буквы, 10 арабских цифр, 30 знаков и символов:
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | ||
| a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z | ||
| + | плюс; | _ | пробел; | ||||||||||||||||||||||||
| - | минус; | ( | левая круглая скобка; | ||||||||||||||||||||||||
| * | звездочка; | ) | правая круглая скобка; | ||||||||||||||||||||||||
| / | косая черта; | [ | левая квадратная скобка; | ||||||||||||||||||||||||
| \ | обратная косая черта; | ] | правая квадратная скобка; | ||||||||||||||||||||||||
| < | меньше; | { | левая фигурная скобка; | ||||||||||||||||||||||||
| > | больше; | } | правая фигурная скобка; | ||||||||||||||||||||||||
| = | равно; | ? | знак вопроса; | ||||||||||||||||||||||||
| . | точка; | ! | восклицательный знак; | ||||||||||||||||||||||||
| , | запятая; | | | вертикальная черта; | ||||||||||||||||||||||||
| ; | точка с запятой; | ~ | волнистая черта; | ||||||||||||||||||||||||
| : | двоеточие; | ^ | угол вверх; | ||||||||||||||||||||||||
| ' | апострόф; | # | решетка; | ||||||||||||||||||||||||
| " | кавычки; | & | амперсант; | ||||||||||||||||||||||||
| _ | подчеркивание; | % | проценты. | ||||||||||||||||||||||||
3.5.2. Простейшие конструкции Си/Си++
Простейшие конструкции алгоритмического языка – аналоги слогов (слов) разговорного языка.
Классификация простейших конструкций по критерию «типовые компоненты» представлена на рис. 3.3.
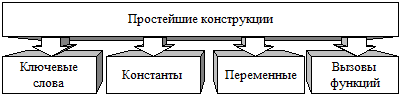
Рис. 3.3. Классификация простейших конструкций Си/Си++
Рассмотрим простейшие конструкции Си/Си++ подробно.
Ключевые слова
Ключевое слово– обозначение стандартного действия (описания) в программировании.
К основным ключевым словам Си/Си++ относятся:
| auto | автоматический | if | если |
| break | завершить | int | целое |
| bool | логический | long | длинное |
| case | вариант | register | регистровый |
| char | символьный | return | возврат |
| continue | продолжить | short | короткий |
| default | по умолчанию | sizeof | размер |
| do | выполнять | static | статический |
| double | двойной точности | struct | структура |
| else | иначе | switch | переключатель |
| entry | вход | typedef | определение типа |
| extern | внешний | union | объединение |
| for | для | unsigned | без знака |
| float | плавающий | void | пустой |
| goto | перейти | while | пока |
Константы
Константа – данное в форме конкретного значения, не меняющееся в процессе выполнения программы.
Большинство констант в Си/Си++ соответствует числам в математике. Дополнительно возможно использование не числовых – текстовых констант.
Константы классифицируются по трём критериям – тип, размер, форма представления.
Тип– основной критерий, определяющий принадлежность константы к конкретной группе (целые, вещественные, текстовые).
Внутри группы применимы два остальных критерия.
Размер– диапазон представления констант.
Форма представления – шаблон записи констант.
Классификация констант по основным критериям представлена на рис. 3.4.
В отличие от математики, в Си/Си++ истинные значения констант – беззнаковые. Положительность (отрицательность) задаётся унарной операцией присвоения знака + (–).
Операция– элементарное действие над данными (операндами).
Операнд– величина (данное), участвующая в операции.
Унарная операция– операция с использованием одного операнда.
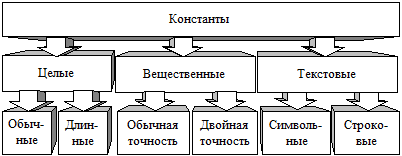
Рис. 3.4. Классификация констант по типам и размерам
Для облегчения перехода от чисел в математике к константам алгоритмического языка будем считать унарные операции формирования знака признаками положительности (отрицательности) константы.
Целые константы
Целая константа – совокупность цифр, предваряемая знаком + (-) или без него.
Константа без знака считается положительной.
Универсальность языка Си/Си++, в частности, обусловлена возможностью работы не только с удобными пользователю-непрофессионалу десятичными числами.
В качестве целых констант используются восьмеричные, десятичные и шестнадцатеричные.
Десятичная целая константа – аналог целого десятичного числа в математике.
Структура десятичной константы:
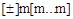
, где m – одна из десятичных цифр константы (0-9);
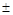– признак положительности (отрицательности);
[ ] – признак необязательности содержимого.
Примеры целых констант: 3, 101, +19, -18640.
Восьмеричная целая константа– конструкция, соответствующая восьмеричному числу в математике.
Структура восьмеричной константы:
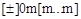
, где 0 – признак восьмеричной константы;
m – одна из восьмеричных цифр константы (0-7);
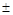– признак положительности (отрицательности);
[ ] – признак необязательности содержимого.
Примеры записи целых восьмеричных чисел и констант представлены в табл. 3.1.
Таблица 3.1
| Числа в математике | Константы в Си/Си++ |
| 12548 | |
| -168 | -016 |
| +101758 | +010175 |
| 08 | |
| -77778 | -07777 |
Шестнадцатеричная целая константа – конструкция, соответствующая шестнадцатеричному числу в математике.
Шестнадцатеричное число в математике компонуется из цифр от 0 до 9 и начальных букв латинского алфавита A, B, C, D, E, F (a, b, c, d, e, f), обозначающих цифры записи десятичных чисел от 10 до 15 соответственно.
ü Внимание! В шестнадцатеричных константах Си/Си++ значения одинаковых прописных и строчных букв идентичны.
Структура шестнадцатеричной константы:
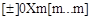или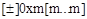 
, где 0X (0x) – признак шестнадцатеричной константы;
m – одна из шестнадцатеричных цифр константы (0-9, A-F, a-f);
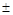– признак положительности (отрицательности);
[ ] – признак необязательности содержимого.
Примеры записи целых шестнадцатеричных чисел и констант представлены в табл. 3.2.
Таблица 3.2
| Числа в математике | Константы в Си/Си++ | |||
| 13516 | 0X135; 0x135 | |||
| +12B716 | +0X12B7; +0x12b7; +0X12b7; +0x12B7 | |||
| -FF16 | -0XFF; -0xff; -0Xff; -0xFF | |||
| A6C316 | 0XA6C3; 0xa6c3; 0Xa6c3; 0xA6C3 | |||
| -016 | -0X0; -0x0 | |||
| +13516 | +0X135; +0x135 | |||
По критерию размер целые константы разделяются на обычные и длинные.
Обычная – константа целого типа, занимающая поле памяти размером в одно слово (в большинстве случаев 2 байта).
Двухбайтовые слова ПЭВМ позволяют рассчитать диапазоны изменения целых констант. Для десятичных диапазон определяется неравенствами:
.
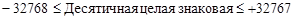
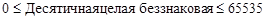Для восьмеричных диапазон определяется неравенствами:
.
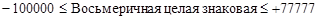
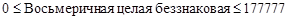Для шестнадцатеричных диапазон определяется неравенствами:
.
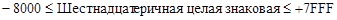
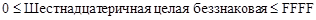При необходимости увеличения диапазона, используются длинные константы.
Длинная– константа целого типа, занимающая поле памяти размером в два слова (чаще размером 4 байта).
Четырёхбайтовые слова ПЭВМ позволяют рассчитать увеличенные (более чем на четыре порядка, конкретно в 65535 раз) диапазоны изменения длинных целых констант.
Так, длинные знаковые целые десятичные константы изменяются в диапазоне от -2147483648 до +2147483647. Беззнаковые – от 0 до 4294967295.
ü Внимание! Выбор размера поля для хранения констант выполняется автоматически в зависимости от числа разрядов константы.
Двойную длину константы (по желанию) можно указать явно. Отличительный признак – буква L (l) в конце константы.
Структуры длинных явно указанных констант имеют вид
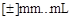или 
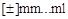
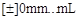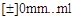
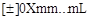или 
или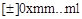 
Примеры длинных явно указанных констант:
1000242L, 047777777l, +12345678L, -0ХА761263l
Вещественные константы
Вещественные константы соответствуют дробным (рациональным) числам в математике.
В математике известны две формы представления дробных чисел: естественная (с фиксированной запятой) и экспоненциальная (с плавающей запятой).
Структура чисел с фиксированной запятой:
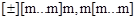
, где m – одна из десятичных цифр дробного числа (0-9);
, – разделитель целой и дробной части числа;
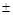– признак положительности (отрицательности);
[ ] – признак необязательности содержимого.
Примеры десятичных чисел с фиксированной запятой:
34,5; -198,67; 0,0042; +1200,0.
Числа с плавающей запятой могут быть представлены обобщённой и развёрнутой структурами.
Обобщённая структура чисел с плавающей запятой:
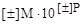
, где M – мантисса числа;
10 – основание системы счисления;
Р – порядок числа;
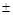– признак положительности (отрицательности);
[ ] – признак необязательности содержимого.
Представив мантиссу M и порядок P детализовано, получим развёрнутую структуру чисел с плавающей запятой:
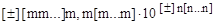
, где m – одна из десятичных цифр мантиссы числа (0-9);
, – разделитель целой и дробной части числа;
10 – основание системы счисления;
n – одна из десятичных цифр порядка (0-9);
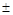– признак положительности (отрицательности);
[ ] – признак необязательности содержимого.
Примеры десятичных чисел с плавающей запятой:
0,3·105 ; +12,72·10-8; -0,0004·1012 ; 0,33·10+3 ; 45,0·10-4 .
Первый сомножитель каждого числа составляет мантисса, показатель степени второго – порядок.
Проанализировав развёрнутую структуру чисел с плавающей запятой, можно сделать вывод о её универсальности. Действительно, при нулевом показателе степени второй сомножитель становится равным единице (100 = 1) и может быть опущен. Следовательно, число с плавающей запятой приобретает структуру числа с фиксированным разделителем. Данная закономерность используется для представления вещественных констант в Си/Си++.
Вещественная константа (константа с плавающей точкой) – аналог дробного (рационального) десятичного числа в математике.
Структуры вещественной константы:
,
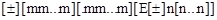
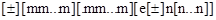где m – одна из десятичных цифр мантиссы числа (0-9);
. – разделитель целой и дробной части мантиссы;
E (e) – обозначение основания десятичной системы счисления;
n – одна из десятичных цифр порядка (0-9);
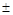– признак положительности (отрицательности);
[ ] – признак необязательности содержимого.
Структура позволяет формировать константы с фиксированной (без экспоненты) и плавающей точкой (с экспонентой). Для констант с фиксированной точкой составляющая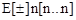 
не указывается. Для констант с плавающей точкой наличие элемента 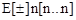обязательно.
ü Внимание! Одна из составляющих мантиссы обязательна в любом из вариантов представления вещественной константы.
Примеры записи вещественных десятичных констант представлены в табл. 3.3.
Таблица 3.3
| Числа в математике | Константы в Си/Си++ |
| 46,2 | 46.2 |
| -135,0 | -135.0; -135. |
| +0,76 | +0.76; 0.76; +.76; .76 |
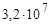 | 3.2E7; 3.2e7 |
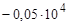 | -0.05E4; -0.05e4; -.05E4; -.05e4 |
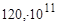 | 120.0E11; 120.0e11; 120.E11; 120.e11; 120E11; 120e11 |
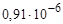 | 0.91E-6; 0.91e-6; .91E-6; .91e-6 |
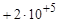 | +2E+5; +2e+5; 2E5; 2e5; 2.E5; 2.e5 |
ü Внимание! Запрещается внутри константы использовать пробелы.
Вещественные константы, как и числа, оцениваются по двум параметрам: диапазону и точности представления.
Диапазон представления констант– разность максимального и минимального значений порядка.
Точность представления констант– определение количества разрядов мантиссы.
В Си/Си++ предусмотрены вещественные константы двух вариантов точности – обычной и двойной.
Вещественные константы обычной точности хранятся в четырёхбайтовых полях памяти в двоичном виде. Первый байт отводится под показатель степени, остальные три – для записи мантиссы.
Следовательно, десятичные константы обычной точности могут содержать не более трёх разрядов порядка (максимум 127) и 7-8 значащих цифр мантиссы.
По форме записи константы могут быть нормализованными или ненормализованными.
Нормализованная– константа с мантиссой в диапазоне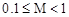 
или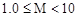 
.
В Си/Си++ используется второй вариант нормализации. Реальный диапазон представления вещественных констант обычной точности составляет ±3.4000000E±38.
Примеры нормализованных констант:
2.3Е2 +7.0Е-4 -1.08Е+6
Вещественные константы двойной точности хранятся в восьмибайтовых полях памяти.
Первые полтора байта отводится под показатель степени, остальные (6,5) для записи мантиссы. Следовательно, десятичные константы двойной точности могут содержать не более четырёх разрядов порядка (максимум 2047) и 16–17 значащих цифр мантиссы.
Реальный диапазон представления нормализованных вещественных констант двойной точности составляет ±1.700000000000000E±308.
ü Внимание! Автоматически вещественные константы помещаются в восьмибайтовые поля памяти, т.е. представляются с двойной степенью точности.
Использование констант с обычной точностью (по желанию) требует явного указания. Отличительный признак константы обычной точности – буква F (f) в конце константы.
Структуры констант с обычной точностью имеют вид:
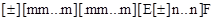
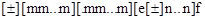
Примеры явного указания обычной точности для вещественных десятичных констант:
101.037F, -15.2f, 0.46578E-2f, +0.000123e6f, -55.3e-12F
Текстовые константы
Текстовая константа– представление символов поэлементно или в совокупности.
Реализуется в виде символьной константы или символьной строки.
Символьная константа – единичный символ, подлежащий обработке.
Обозначение символьной константы оформляется структурой:
‘c’
, где c –символ, составляющий константу;
‘ – ограничители символа (константы).
В качестве символа (с) может использоваться любой элемент алфавита Си/Си++ или клавиатуры, за исключением апострофа (‘) и обратной косой черты (\).
Примеры записи символьных констант:
‘A’; ‘.’; ‘a’; ‘4’; ‘ю’; ‘+’; ‘]’; ‘%’.
Символы апостроф «‘» и обратная косая черта «\» обозначаются символьными константами ‘\’’ и ‘\\’.
Каждая символьная константа помимо обозначения имеет числовое значение. Значение символьной константы – ее целочисленный восьмеричный код.
Код символьной константы с предшествующим знаком \ (обратная косая черта) допускается применять вместо символа. Это удобно для обозначения не выводимых на печать символов. Например, звуковому сигналу соответствует код 007. При записи восьмеричного кода левые незначащие нули можно не указывать. Так, символьные константы ‘\007’, ‘\07’, ‘\7’ являются идентичными.
ü Внимание! Коды цифр не совпадают с их обозначением. Например, символу '4' соответствует код '\064'.
К невидимым символам, наряду со звуковым сигналом, относятся управляющие последовательности.
Управляющая – последовательность обратной косой черты и буквы, предписывающая некоторое типовое действие.
Обозначения некоторых управляющих последовательностей представлены в табл. 3.4
Таблица 3.4
| Обозначение | Наименование | Выполняемое действие |
| \n | Новая строка (перевод каретки) | Переход в начало новой строки |
| \t | Табуляция | Перемещение курсора (печатающей головки) на 8 позиций вправо |
| \b | Шаг назад | Сдвиг курсора влево на одну позицию |
| \r | Возврат каретки | Перемещение курсора в начало текущей строки |
Таким образом, обозначения 'A', '\007', '\t' есть символьные константы, а содержимое в апострофах рассматривается как один символ.
Коды символьных констант занимают однобайтовые поля памяти. Поэтому максимально возможное количество различных символов равно 256. Коды символов представлены в технической документации.
Символьная строка – последовательность подлежащих обработке символов, заключенная в кавычки.
Структура символьной строки
“c[c…c]”
, где c – один из символов, составляющий текстовую константу;
“ – ограничители символьной строки;
[ ] – признак необязательности содержимого.
ü Внимание! В символьной строке в качестве символов (с) может использоваться любой элемент алфавита Си/Си++ или клавиатуры.
Типичные примеры:
“А12” “Александр” “Михаил Владимирович”
“Константа +146 является целочисленной десятичной”
Кавычки не являются частью строки, а отмечают ее начало и конец. Если в состав символьной строки входят символы “, ‘, \, то они записываются в виде \”, \’, \\. Так, предложение – «Запомните, символ \ называется “обратная косая черта”» –реализуется символьной строкой:
“Запомните, символ \\ называется \”обратная косая черта\””
Символьная строка занимает последовательность соседних однобайтовых полей памяти, число которых соответствует количеству хранимых символов плюс символ конца строки ‘\0’ (нуль-символ).
ü Внимание! Общая длина поля для хранения символьной строки всегда превышает на 1 байт число символов в ней.
Нуль-символ не выводится на печать, но автоматически добавляется в конец строки оператором ввода. Так, текстовые константы ‘T’ и “T” по виду, (не считая ограничителей) совершенно одинаковы, но в первом случае это символьная константа, для хранения которой нужен один байт, а во втором случае – символьная строка из символа «T» и нуль-символа (\0). Для хранения этой строки потребуется два байта.
Переменные
Переменная– именованное данное, значение которого в процессе выполнения программы может изменяться.
Имя (идентификатор) переменной– уникальная последовательность букв и цифр алфавита Си/Си++, начинающаяся с буквы.
Символ подчеркивания ( _ ) считается буквой. Количество символов в идентификаторе не ограничивается, но значимыми являются первые восемь.
Идентификаторы переменных составляются пользователем. Каждый из них (с учётом ограничений по правилам составления), должен соответствовать обозначению данного.
Физически переменная представляет собой ячейку памяти для хранения значения (константы).
Логически идентификатор есть уникальное обозначение, позволяющее отличить одну ячейку от другой.
Примеры записи идентификаторов:
a, d17, XoD, _T62, SUMMA, b_at, x100, a_12_b.
ü Внимание! При составлении имён переменных строчные и прописные буквы не идентичны.
Следовательно, обозначения GAMMA, gamma и Gamma описывают три разные переменные.
Имя определяет ячейку для хранения численного значения переменной.
ü Внимание! Запрещается использование ключевых слов в качестве имен переменных.
Варианты классификации переменных по критериям «назначение», «тип», «вид» представлены на рис. 3.5.
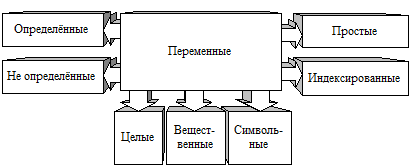Рис. 3.5. Схема классификации переменных
По критерию назначение переменная может быть определённой или неопределённой.
Определенная– переменная, значение которой сформировано пользователем (находится в виде константы в ячейке с заданным именем).
Неопределенная– переменная, значение которой случайно (не сформировано пользователем).
По критерию «вид» переменные делятся на простые и индексированные.
Простая– переменная, предназначенная для хранения единичного данного и обозначенная только идентификатором.
Индексированная– переменная, определяющая элемент массива и обозначенная идентификатором с индексом (индексами).
Рассмотрим правила использования простых переменных (индексированные переменные изложены в разд. 5.2).
Переменные, по определению, есть поименованные ячейки для хранения констант. Следовательно, по критерию «тип» они также должны быть:
· целыми (обычными и длинными);
· вещественными (обычной и двойной точности);
· текстовыми (символьными).
Исключением является, символьная строка. По способу хранения символьная строка аналогична одномерному массиву (разд. 5.2).
Целая– переменная для хранения целой константы.
Целые переменные могут быть знаковые и беззнаковые.
Символьная– переменная для хранения символьной константы.
Вещественная– переменная для хранения вещественной константы.
ü Внимание! Типы переменных должны быть заданы явно (объявлены), в отличие от констант (типы определяются формой записи).
Объявление типов переменных производится с помощью описателей.
Описатель – форма явного обозначения однотипных переменных.
Каждый описатель оформляется в виде оператора и в простейшем варианте имеет структуру:
описатель u1 [, u2, ..., ui, ..., uN];
, где описатель – ключевое слово, определяющее тип переменных;
_ – разделитель описателя и списка переменных;
u1, ui, uN – идентификаторы объявляемых переменных;
, , – разделители переменных в списке;
[ ] – признак необязательности содержимого;
; – символ простого оператора.
Основными описателями являются ключевые слова: int (целый), long (длинный), float (плавающий), double (двойная точность), char (символьный).
Дополнительными могут быть – signed (со знаком), unsigned (без знака), и short (короткий).
ü Внимание! Автоматически все переменные считаются знаковыми.
Описатель определяет, к какому типу относится переменная, т.е. для хранения какой константы она предназначена.
Типы переменных задают размеры ячеек для хранения их значений. Для большинства ЭВМ соотношение типов и размеров представлено в табл. 3.5.
Таблица 3.5
| Описатель | Наименование типа | Число байт (бит) |
| short int | Короткий целый | 2 (16) |
| int | Целый | 2 (16) |
| long int | Длинный целый | 4 (32) |
| float | Плавающая точка | 4 (32) |
| double | Двойная точность | 8 (64) |
| char | Символьный | 1 (8) |
Анализ первых строк таблицы показывает: целое и короткое целое по размеру отводимой ячейки памяти идентичны. Поэтому описатель short int, как правило, не применяется.