Анализ трудоемкости рекурсивных алгоритмов методом подсчета вершин дерева рекурсии
Рекурсивные алгоритмы относятся к классу алгоритмов с высокой ресурсоемкостью, так как при большом количестве самовызовов рекурсивных функций происходит быстрое заполнение стековой области. Кроме того, организация хранения и закрытия очередного слоя рекурсивного стека являются дополнительными операциями, требующими временных затрат. На трудоемкость рекурсивных алгоритмов влияет и количество передаваемых функцией параметров.
Рассмотрим один из методов анализа трудоемкости рекурсивного алгоритма, который строится на основе подсчета вершин рекурсивного дерева. Для оценки трудоемкости рекурсивных алгоритмов строится полное дерево рекурсии. Оно представляет собой граф, вершинами которого являются наборы фактических параметров при всех вызовах функции, начиная с первого обращения к ней, а ребрами – пары таких наборов, соответствующих взаимным вызовам. При этом вершины дерева рекурсии соответствуют фактическим вызовам рекурсивных функций. Следует заметить, что одни и те же наборы параметров могут соответствовать разным вершинам дерева. Корень полного дерева рекурсивных вызовов – это вершина полного дерева рекурсии, соответствующая начальному обращению к функции.
Важной характеристикой рекурсивного алгоритма является глубина рекурсивных вызовов – наибольшее одновременное количество рекурсивных обращений функции, определяющее максимальное количество слоев рекурсивного стека, в котором осуществляется хранение отложенных вычислений. Количество элементов полных рекурсивных обращений всегда не меньше глубины рекурсивных вызовов. При разработке рекурсивных программ необходимо учитывать, что глубина рекурсивных вызовов не должна превосходить максимального размера стека используемой вычислительной среды.
При этом объем рекурсии - это одна из характеристик сложности рекурсивных вычислений для конкретного набора параметров, представляющая собой количество вершин полного рекурсивного дерева без единицы.
Будем использовать следующие обозначения для конкретного входного параметра D:
R(D) – общее число вершин дерева рекурсии,
RV(D) – объем рекурсии без листьев (внутренние вершины),
RL(D) – количество листьев дерева рекурсии,
HR(D) – глубина рекурсии.
Например, для вычисления n -го члена последовательности Фибоначчи разработана следующая рекурсивная функция:
int Fib(int n){ //n – номер члена последовательности
if(n<3) return 1; //база рекурсии
return Fib(n-1)+Fib(n-2); //декомпозиция
}
Тогда полное дерево рекурсии для вычисления пятого члена последовательности Фибоначчи будет иметь вид (рис. 34.1):
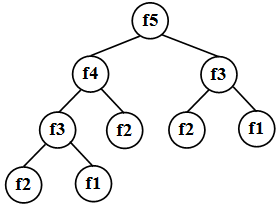
Рис. 34.1. Полное дерево рекурсии для пятого члена последовательности Фибоначчи
Характеристиками рассматриваемого метода оценки алгоритма будут следующие величины.
| D = 5 | D = n |
| R(D)=9 | R(D)=2fn-1 |
| RV(D)=4 | RV(D)=fn-1 |
| RL(D)=5 | RL(D)=fn |
| HR(D)=4 | HR(D)=n-1 |
Пример 1. Задача о разрезании прямоугольника на квадраты.
Дан прямоугольник, стороны которого выражены натуральными числами. Разрежьте его на минимальное число квадратов с натуральными сторонами. Найдите число получившихся квадратов.
Разработаем рекурсивную триаду.
Параметризация: m, n – натуральные числа, соответствующие размерам прямоугольника.
База рекурсии: для m=n число получившихся квадратов равно 1, так как данный прямоугольник уже является квадратом.
Декомпозиция: если 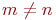 , то возможны два случая m < n или m > n. Отрежем от прямоугольника наибольший по площади квадрат с натуральными сторонами. Длина стороны такого квадрата равна наименьшей из сторон прямоугольника. После того, как квадрат будет отрезан, размеры прямоугольника станут следующие: большая сторона уменьшится на длину стороны квадрата, а меньшая не изменится. Число искомых квадратов будет вычисляться как число квадратов, на которые будет разрезан полученный прямоугольник, плюс один (отрезанный квадрат). К получившемуся прямоугольнику применим аналогичные рассуждения: проверим на соответствие базе или перейдем к декомпозиции (рис. 34.2).
, то возможны два случая m < n или m > n. Отрежем от прямоугольника наибольший по площади квадрат с натуральными сторонами. Длина стороны такого квадрата равна наименьшей из сторон прямоугольника. После того, как квадрат будет отрезан, размеры прямоугольника станут следующие: большая сторона уменьшится на длину стороны квадрата, а меньшая не изменится. Число искомых квадратов будет вычисляться как число квадратов, на которые будет разрезан полученный прямоугольник, плюс один (отрезанный квадрат). К получившемуся прямоугольнику применим аналогичные рассуждения: проверим на соответствие базе или перейдем к декомпозиции (рис. 34.2).
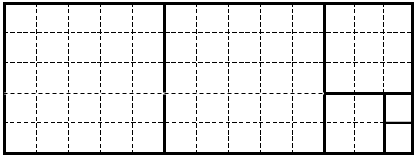
Рис. 34.2. Пример разрезания прямоугольника 13x5 на квадраты
#include "stdafx.h"
#include <iostream>
using namespace std;
int kv(int m,int n);
int _tmain(int argc, _TCHAR* argv[]) {
int a,b,k;
printf("Введите стороны прямоугольника->");
scanf("%d%d",&a,&b);
k = kv(a,b);
printf("Прямоугольник со сторонами %d и %d можно разрезать
на %d квадратов",a,b,k);
system("pause");
return 0;
}
int kv(int m,int n){ //m,n – стороны прямоугольника
if(m==n) return 1; //база рекурсии
if(m>n) return 1+kv(m-n,n); //декомпозиция для m>n
return 1+kv(m,n-m); //декомпозиция для m<n
}
Характеристиками рассматриваемого метода оценки алгоритма будут следующие величины (рис. 34.3).
| D = (13, 5) | D = (m, n), m 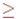 n, худший случай n, худший случай |
| R(D)=6 | R(D)=m |
| RV(D)=4 | RV(D)=m-2 |
| RL(D)=1 | RL(D)=1 |
| HR(D)=6 | HR(D)=m |
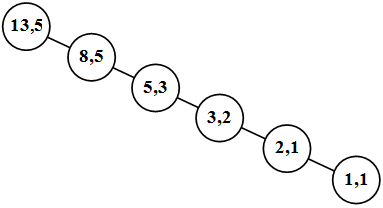
Рис. 34.3. Пример полного дерева рекурсии для разрезания прямоугольника 13x5 на квадраты
Пример 2. Задача о нахождении центра тяжести выпуклого многоугольника.
Выпуклый многоугольник задан на плоскости координатами своих вершин. Найдите его центр тяжести.
Разработаем рекурсивную триаду.
Параметризация: x, y – вещественные массивы, в которых хранятся координаты вершин многоугольника; n – это число вершин многоугольника, по условию задачи, n>1 так как минимальное число вершин имеет двуугольник (отрезок).
База рекурсии: для n=2 в качестве многоугольника рассматривается отрезок, центром тяжести которого является его середина (рис. 4А). При этом середина делит отрезок в отношении 1 : 1. Если координаты концов отрезка заданы как (x0,y0) и (x1,y1), то координаты середины вычисляются по формуле:
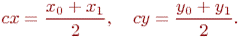
Декомпозиция: если n>2, то рассмотрим последовательное нахождение центров тяжести треугольника, четырехугольника и т.д.
Для n=3 центром тяжести треугольника является точка пересечения его медиан, которая делит каждую медиану в отношении 2 : 1, считая от вершины. Но основание медианы – это середина отрезка, являющегося стороной треугольника. Таким образом, для нахождения центра тяжести треугольника необходимо: найти центр тяжести стороны треугольника (отрезка), затем разделить в отношении 2 : 1, считая от вершины, отрезок, образованный основанием медианы и третьей вершиной (рис. 4B).
Для n=3 центром тяжести четырехугольника является точка, делящая в отношении 3 : 1, считая от вершины, отрезок: он образован центром тяжести треугольника, построенного на трех вершинах, и четвертой вершиной (рис. 4C).
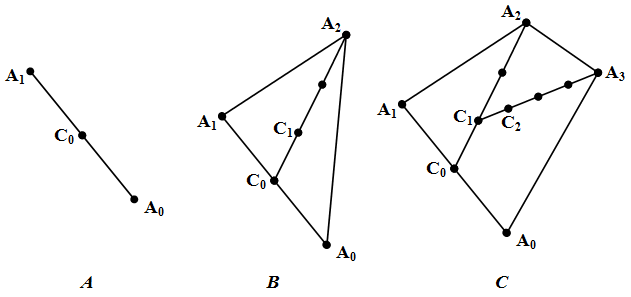
Рис. 34.4. Примеры построения центров тяжести многоугольников
Таким образом, для нахождения центра тяжести n -угольника необходимо разделить в отношении (n-1): 1, считая от вершины, отрезок: он образован центром тяжести (n-1) -угольника и n -ой вершиной рассматриваемого многоугольника. Если концы отрезка заданы координатами вершины (xn,yn) и центра тяжести (n-1) -угольника (cxn-1,cyn-1), то при делении отрезка в данном отношении получаем координаты:
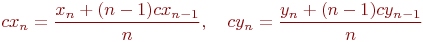
#include "stdafx.h"
#include <iostream>
using namespace std;
#define max 20
void centr(int n,float *x, float *y, float *c);
int _tmain(int argc, _TCHAR* argv[]){
int m, i=0;
FILE *f;
if ( ( f = fopen("in.txt", "r") ) == NULL )
perror("in.txt");
else {
fscanf(f, "%d",&m);
printf("\n%d",m);
if ( m < 2 || m > max ) //вырожденный многоугольник
printf ("Вырожденный многоугольник");
else {
float *px,*py,*pc;
px = new float[m];
py = new float[m];
pc = new float[2];
pc[0] = pc[1] = 0;
while(i<m) {
fscanf(f, "%f %f",&px[i], &py[i]);
printf("\n%f %f",px[i], py[i]);
i++;
}
centr(m,px,py,pc);
printf ("\nЦентр тяжести имеет координаты:
(%.4f, %.4f)",pc[0],pc[1]);
delete [] pc;
delete [] py;
delete [] px;
}
fclose(f);
}
system("pause");
return 0;
}
void centr(int n,float *x, float *y, float *c){
//n - количество вершин,
//x,y - координаты вершин,
//c - координаты центра тяжести
if(n==2){ //база рекурсии
c[0]=(x[0]+x[1])/2;
c[1]=(y[0]+y[1])/2;
}
if(n>2) { //декомпозиция
centr(n-1,x,y,c);
c[0]= (x[n-1] + (n-1)*c[0])/n;
c[1]= (y[n-1] + (n-1)*c[1])/n;
}
}
Характеристиками рассматриваемого метода оценки алгоритма будут следующие величины.
| D = 4 | D = n |
| R(D)=3 | R(D)=n-1 |
| RV(D)=1 | RV(D)=n-3 |
| RL(D)=1 | RL(D)=1 |
| HR(D)=3 | HR(D)=n-1 |
Однако в данном случае для более достоверной оценки необходимо учитывать емкостные характеристики алгоритма.
Пример 3. Задача о разбиении целого на части.
Найдите количество разбиений натурального числа на сумму натуральных слагаемых.
Разбиение подразумевает представление натурального числа в виде суммы натуральных слагаемых, при этом суммы должны отличаться набором чисел, а не их последовательностью. В разбиение также может входить одно число.
Например, разбиение числа 6 будет представлено 11 комбинациями:
5+1
4+2, 4+1+1
3+3, 3+2+1, 3+1+1+1
2+2+2, 2+2+1+1, 2+1+1+1+1
1+1+1+1+1+1
Рассмотрим решение в общем виде. Пусть зависимость R(n,k) вычисляет количество разбиений числа n на сумму слагаемых, не превосходящих k. Опишем свойства R(n,k).
Если в сумме все слагаемые не превосходят 1, то такое представление единственно, то есть R(n,k)=1.
Если рассматриваемое число равно 1, то при любом натуральном значении второго параметра разбиение также единственно: R(n,k)=1.
Если второй параметр превосходит значение первого , то имеет место равенство R(n,k)=R(n,n), так как для представления натурального числа в сумму не могут входить числа, превосходящие его.
Если в сумму входит слагаемое, равное первому параметру, то такое представление также единственно (содержит только это слагаемое), поэтому имеет место равенство: R(n,n)=R(n,n-1)+1.
Осталось рассмотреть случай (n>k). Разобьем все представления числа n на непересекающиеся разложения: в одни обязательно будет входить слагаемое k, а другие суммы не содержат k. Первая группа сумм, содержащая k, эквивалентна зависимости R(n-k,k), что следует после вычитания числа k из каждой суммы. Вторая группа сумм содержит разбиение числа n на слагаемые, каждое из которых не превосходит k-1, то есть число таких представлений равно R(n,k-1). Так как обе группы сумм не пересекаются, то R(n,k)=R(n-k,k)+R(n,k-1).
Разработаем рекурсивную триаду.
Параметризация: Рассмотрим разбиение натурального числа n на сумму таких слагаемых, которые не превосходят натурального числа k.
База рекурсии: исходя из свойств рассмотренной зависимости, выделяются два базовых случая:
при n=1 R(n,k)=1,
при k=1 R(n,k)=1.
Декомпозиция: общий случай задачи сводится к трем случаям, которые и составляют декомпозиционные отношения.
при n=k R(n,k)=R(n,n-1)+1,
при n<k R(n,k)=R(n,n),
при n>k R(n,k)=R(n-k,k)+R(n,k-1).
#include "stdafx.h"
#include <iostream>
using namespace std;
unsigned long int Razbienie(unsigned long int n,
unsigned long int k);
int _tmain(int argc, _TCHAR* argv[]){
unsigned long int number, max,num;
printf ("\nВведите натуральное число: ");
scanf ("%d", &number);
printf ("Введите максимальное натуральное слагаемое в
сумме: ");
scanf ("%d", &max);
num=Razbienie(number,max);
printf ("Число %d можно представить в виде суммы с
максимальным слагаемым %d.", number, max);
printf ("\nКоличество разбиений равно %d",num);
system("pause");
return 0;
}
unsigned long int Razbienie(unsigned long int n,
unsigned long int k){
if(n==1 || k==1) return 1;
if(n<=k) return Razbienie(n,n-1)+1;
return Razbienie(n,k-1)+Razbienie(n-k,k);
}
Пример 4. Задача о переводе натурального числа в шестнадцатеричную систему счисления.
Дано натуральное число, не выходящее за пределы типа unsigned long. Число представлено в десятичной системе счисления. Переведите его в систему счисления с основанием 16.
Пусть требуется перевести целое число n из десятичной в р -ичную систему счисления (по условию задачи, р = 16), то есть найти такое k, чтобы выполнялось равенство n10=kp.
Параметризация: n – данное натуральное число, р – основание системы счисления.
База рекурсии: на основании правил перевода чисел из десятичной системы в систему счисления с основанием р, деление нацело на основание системы выполняется до тех пор, пока неполное частное не станет равным нулю, то есть: если целая часть частного n и р равна нулю, то k = n. Данное условие можно реализовать иначе, сравнив n и р: целая часть частного равна нулю, если n < р.
Декомпозиция: в общем случае k формируется из цифр целой части частного n и р, представленной в системе счисления с основанием р, и остатка от деления n на p.
#include "stdafx.h"
#include <iostream>
using namespace std;
#define maxline 50
void perevod( unsigned long n, unsigned int p,FILE *pf);
int _tmain(int argc, _TCHAR* argv[]){
unsigned long number10;
unsigned int osn=16;
char number16[maxline];
FILE *f;
if ((f=fopen("out.txt", "w"))==NULL)
perror("out.txt");
else {
printf ("\nВведите число в десятичной системе: ");
scanf("%ld", &number10);
perevod(number10, osn, f);
fclose(f);
}
if ((f=fopen("out.txt", "r"))==NULL)
perror("out.txt");
else {
fscanf(f,"%s",number16);
printf("\n %ld(10)=%s(16)", number10, number16);
fclose(f);
}
system("pause");
return 0;
}
void perevod(unsigned long n, unsigned int p, FILE *pf){
char c;
unsigned int r;
if(n >= p) perevod (n/p, p, pf);//декомпозиция
r=n%p;
c=r < 10 ? char (r+48) : char (r+55);
putc(c, pf);
}
Ключевые термины
База рекурсии – это тривиальный случай, при котором решение задачи очевидно, то есть не требуется обращение функции к себе.
Глубина рекурсивных вызовов – это наибольшее одновременное количество рекурсивных обращений функции, определяющее максимальное количество слоев рекурсивного стека.
Декомпозиция – это выражение общего случая через более простые подзадачи с измененными параметрами.
Корень полного дерева рекурсивных вызовов – это вершина полного дерева рекурсии, соответствующая начальному обращению к функции.
Косвенная (взаимная) рекурсия – это последовательность взаимных вызовов нескольких функций, организованная в виде циклического замыкания на тело первоначальной функции, но с иным набором параметров.
Объем рекурсии - это характеристика сложности рекурсивных вычислений для конкретного набора параметров, представляющая собой количество вершин полного рекурсивного дерева без единицы.
Параметризация – это выделение из постановки задачи параметров, которые используются для описания условия задачи и решения.
Полное дерево рекурсии – это граф, вершинами которого являются наборы фактических параметров при всех вызовах функции, начиная с первого обращения к ней, а ребрами – пары таких наборов, соответствующих взаимным вызовам.
Прямая рекурсия – это непосредственное обращение рекурсивной функции к себе, но с иным набором входных данных.
Рекурсивная триада – это этапы решения задач рекурсивным методом.
Рекурсивная функция – это функция, которая в своем теле содержит обращение к самой себе с измененным набором параметров.
Рекурсивный алгоритм – это алгоритм, в определении которого содержится прямой или косвенный вызов этого же алгоритма.
Рекурсия – это определение объекта посредством ссылки на себя.
Краткие итоги
- Рекурсия характеризуется определением объекта посредством ссылки на себя.
- Рекурсивные алгоритмы содержат в своем теле прямое или опосредованное обращение с самим себе.
- Рекурсивные функции содержат в своем теле обращение к самим себе с измененным набором параметров в виде прямой рекурсии. При этом обращение к себе может быть организовано посредством косвенной рекурсии – через цепочку взаимных обращений функций, замыкающихся в итоге на первоначальную функцию.
- Решение задач рекурсивными способами проводится посредством разработки рекурсивной триады.
- Целесообразность применения рекурсии в программировании обусловлена спецификой задач, в постановке которых явно или опосредовано указывается на возможность сведения задачи к подзадачам, аналогичным самой задаче.
- Рекурсивные методы решения задач широко используются при моделировании задач из различных предметных областей.
- Рекурсивные алгоритмы относятся к ресурсоемким алгоритмам. Для оценки сложности рекурсивных алгоритмов учитывается число вершин полного рекурсивного дерева, количество передаваемых параметров, временные затраты на организацию стековых слоев.
