Пример оформления отчета по задаче 1

Задача 1. Постановка задачи: дан ряд 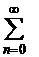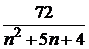. Найти сумму ряда S аналитически. Вычислить значения частичных сумм ряда S_N= 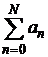и найти величину абсолютной и относительной погрешностей погрешностей при значениях N=10, 10², 10³, 10⁴, 10⁵. Построить гистограммы зависимости погрешностей и количества верных цифр результата от N.

Аналитическое решение задачи (только если не получилось в Mathcad):

S_N= =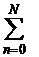

,

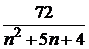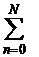
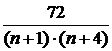
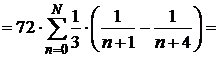
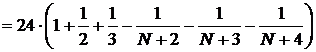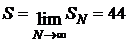. ОТВЕТ: S =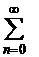 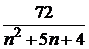= 44.

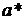Теоретический материал. Пусть - точное значение, - приближенное значение некоторой величины. Абсолютной погрешностью приближенного значения 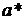называется величина 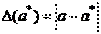. Относительной погрешностью значения 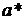(при 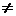0) называется величина 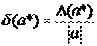. Так как значение как правило неизвестно, чаще получают оценки погрешностей вида: 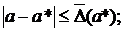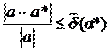. Величины 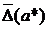и 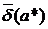называют верхними границами (или просто границами) абсолютной и относительной погрешностей.

Значащую цифру числа 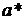называют верной, если абсолютная погрешность числа не превосходит единицы разряда, соответствующего этой цифре.

Введем функцию S(N)= 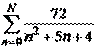. Тогда абсолютную погрешность можно определить с помощью функции d(N) = .

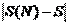Вычисления в MATHCAD приведены в файле «таком-то» (см. фрагмент программы на MATHCAD)

Указание. Предварительно ознакомьтесь с форматами представления результатов.

Результаты вычислительного эксперимента:

Частная сумма	Абсолютная погрешность	Относительная погрешность	Верные цифры числа
S(10)=38.439560439		0.01	4´101
S(100)=43.3009269	0.7	0.02
S(1000)=43.9282153	0.07	0.002	43.9
S(10000)=43.992802	0.007	0.0002	43.99
S(100000)=43.9992802159957	0.0007	0.00002	43.999

Здесь следует описать, как вы определили количество верных цифр.

Вывод: Сформулировать самостоятельно

ПРИЛОЖЕНИЕ 3

Задача 3. Постановка задачи: для пакета MATHCAD найти значения машинного нуля, машинной бесконечности, машинного эпсилон.

Фрагмент текста программы в системе MATHCAD:

Искомые величины в MATHCAD найдены методом простого перебора.

Выводы сформулировать самостоятельно.

Примеры решения задач

Задача 1.

Округлить сомнительные цифры приближенного числа x с относительной погрешностью d, оставив в его записи только верные цифры. x = 42.221, d = 0.5%.

Решение:

1) Найдем количество верных цифр числа x:

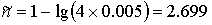
Отсюда n = 3

2) Округляем x до трех цифр

x = 42.2

Задача 2.

Записать формулу для оценки абсолютной погрешностей функции трех переменных:

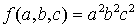, если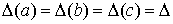

Решение:

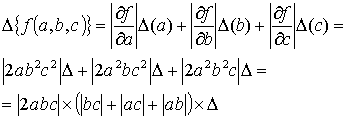
Задача 3.

Дано точное число b и приближенное число x с погрешностью . Указать правило оценки абсолютной и относительной погрешностей функции: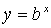

Решение:

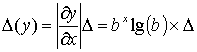
Задача 4.

Дано число a = 547.78, определенное с абсолютной погрешностью 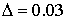. Определить количество верных цифр числа а.

Решение:

1) Найдем относительную погрешность числа

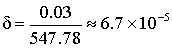
2) Найдем количество верных цифр

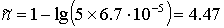
Отсюда n = 4, a = 547.8

Приложение.