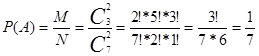Вычисление вероятностей событий по классической формуле определения вероятностей
Классическое определение вероятности: вероятность Р(А) события А равна отношению числа возможных результатов опыта (М), благоприятствующих событию А, к числу всех возможных результатов опыта (N):
.
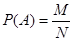Задача 2.Набирая номер телефона, абонент забыл две последние цифры. Какова вероятность того, что он с первого раза наберёт эти цифры правильно, если он помнит, что они различны?
Решение.Обозначим А – событие, состоящее в том, что абонент, набрав произвольно две цифры, угадал их правильно. М – число правильных вариантов, очевидно, что М=1; N – число различных цифр,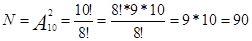 
. Таким образом, Р(А)=M/N=1/90.
Задача 3.Шесть шариков случайным образом располагаются в шести ящиках так, что для каждого шарика равновероятно попадание в любой ящик и в одном ящике может находиться несколько шариков.Какова вероятность того, что в каждом ящике окажется по одному шарику?
Решение.Событие А – в каждом ящике по одному шарику. М – число вариантов распределения шариков, при которых в каждый ящик попадает по одному шарику, М=6! (число способов переставить между собой 6 элементов). N – общее число вариантов N=66 (так как каждый шарик может попасть в каждый из ящиков). В результате получаем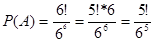 
.
Задача 4.В урне 3 белых и 4 чёрных шара. Из урны вынимаются два шара. Найти вероятность того, что оба шара будут белыми.
Решение.Обозначим: А – событие, состоящее в появлении белых шаров; N – число способов вытащить 2 шара из 7;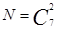 
; M – число способов вытащить 2 белых шара из имеющихся 3 белых шаров; 
.
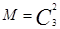