Векторные диаграммы Спираль Френеля

Введение зон Френеля позволяет графически анализировать дифракционные явления. Вычисление результирующего светового поля, описываемого интегралом Гюйгенса-Френеля (2.1), по сути дела сводится к суммированию световых колебаний, возбуждаемых элементарными вторичными источниками. С математической точки зрения задача сводится к суммированию гармонических колебаний, имеющих одну и же частоту, но разные амплитуды и фазы. Это можно сделать графическим способом с помощью построения спирали Френеля.

Рассмотрим графический метод сложения амплитуд. В этом простом и наглядном методе полуволновую зону Френеля мысленно разбивают на весьма узкие кольцевые подзоны. Амплитуду колебаний, создаваемых каждой из таких подзон, изобразим элементарным вектором 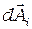. Вследствие увеличения расстояния 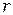и уменьшения коэффициента 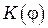,амплитуда колебаний, создаваемых каждой следующей узкой кольцевой зоной, будет убывать по модулю и отставать по фазе от колебаний, создаваемых предыдущей зоной. Изобразив отставание по фазе поворотом каждого вектора 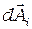против часовой стрелки на соответствующий угол, получим цепочку векторов, векторная сумма которых и есть результирующая амплитуда колебаний в точке Р.

На рис. 4.1а показан результат действия 1-й зоны Френеля. Здесь амплитуда колебаний 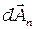от узкого кольца, прилегающего к границе 1-й зоны Френеля, отстает по фазе на 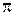от амплитуды колебаний, приходящих в точку 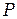из центра 1-й зоны — от 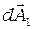поэтому соответствующие этим амплитудам векторы взаимно противоположны по направлению.

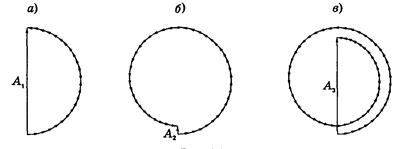
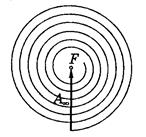
Рис. 4.1. Рис. 4.2.

Продолжая построение, получим векторную диаграмму для результирующей амплитуды колебаний в точке Р от действия первых двух зон Френеля (рис. 4.1б), затем от первых трех зон Френеля (рис. 4.1в) и т. д.Цепочка по мере увеличения числа узких кольцевых зон будет закручиваться в спираль. В результате амплитуда от действия всех зон (всей волновой поверхности) будет равна вектору 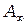, соединяющему начало первой зоны с точкой F – фокусом спирали (рис. 4.2). Длина этого вектора, т.е. амплитуда колебаний в точке Р от полностью открытой волновой поверхности, согласно представлениям Френеля, равна 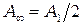,а интенсивность 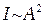в четыре раза меньше, чем при наличии экрана с круглым отверстием, открывающем только 1-ю зону Френеля.

Эту спираль называют спиралью Френеля.Забегая вперед, отметим, что в эксперименте дифракция Френеля связана с действием лишь нескольких первых витков спирали.

Таким образом, амплитуда колебаний и интенсивность света в точке 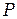по мере увеличения радиуса отверстия в экране изменяется не монотонно. Пока открывается первая зона Френеля, амплитуда в точке 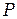увеличивается и достигает максимума при полностью открытой зоне (см. рис. 4.1а). Но по мере открывания второй зоны Френеля амплитуда колебаний в точке 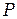убывает, и при полностью открытых двух первых зонах уменьшается почти до нуля (рис. 4.1б). Затем амплитуда увеличивается снова (рис.4.1в) и т. д. То же самое будет наблюдаться, если вместо увеличения отверстия приближать к нему точку наблюдения 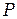вдоль прямой РО (см. рис. 3.1). Это легко понять из данного рисунка: при этом число открываемых зон Френеля в отверстии экрана 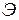будет увеличиваться.

На первый взгляд эти результаты, предсказанные на основе принципа Гюйгенса - Френеля, выглядят парадоксальными. Однако они хорошо подтверждаются опытом. В то же время согласно геометрической оптике интенсивность света в точке 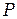не должна зависеть от радиуса отверстия. Особенно неожиданным в методе Френеля представляется тот удивительный вывод, чтопри отверстии в экране, открывающем для точки 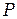две зоны Френеля, интенсивность в этой точке падает практически до нуля, хотя световой поток через отверстие оказывается вдвое больше (рис. 4.1б).

Таким образом, как следует из рис. 4.2 амплитуда результирующего поле в точке 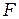(фокусе спирали Френеля) при 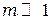равна:

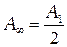. (4.1)