Часть III. Сбор, подготовка и анализ данных. Окончание табл. 19 Матрица факторных нагрузок после вращения факторов Фактор 1 Фактор 2 V} 0,962 - 0,027

Окончание табл. 19

Матрица факторных нагрузок после вращения факторов
	Фактор 1	Фактор 2
V}	0,962	- 0,027
1/2	- 0,057	0,848
Уз	0,934	-0,146
1/4	- 0,098	0,854
1/5	- 0,933	- 0,084
V,	0,083	0,885
Матрица коэффициентов значения факторов
	Фактор 1	Фактор 2
l/i	0,358	0,011
1/2	- 0,001	0,375
1/з	0,345	- 0,043
1/4	-0,017	0,377
1/5	- 0,350	- 0,059
1/6	0,052	0,395
Вычисленная корреляционная матрица
	V/ 1/г	Уз У 4 У 5	VS
V^	0,926* 0,024	- 0,029 0,031 0,038	- 0,053
1/2	- 0,078 0,723*	0,022 -0,158 0,038	-0,105
1/3	0,902 -0,177	0,894* - 0,031 0,081	0,033
1/4	-0,117 0,730	-0,217 0,739* -0,027	-0,107
Vs	-0,895 -0,018	- 0,859 0,020 0,878*	0,016
Vb	0,057 0,746	-0,051 0,748 -0,152 .	0,790*

*Нижний левый треугольник содержит вычисленную корреляционную матрицу; диагональ - общности; верхний правый тре­угольник — остатки между наблюдаемыми и вычисленными корреляциями.

Определение метода факторного анализа

Поскольку установлено, что факторный анализ подходит для анализа данных, необходим^ выбрать соответствующий метод его выполнения. Различные методы факторного анализа раз личают в зависимости от подходов, используемых для выделения коэффициентов значение факторов. Существует два метода — анализ главных компонент и анализ общих факторов. Пр! анализе главных компонент (principal components analysis) учитывают всю дисперсию данных.

Анализ главных компонент (principal components analysis)

Метод факторного анализа, который учитывает всю дисперсию данных.

Диагональ корреляционной матрицы состоит из единиц, и вся дисперсия.введена в матри цу факторных нагрузок. Анализ главных компонент рекомендуется выполнять, если основная задача исследователя — определение минимального числа факторов, которые вносят макси мальный вклад в дисперсию данных, чтобы в последующем использовать их в многомернох анализе. Эти факторы называют главными компонентами (principal component).

В анализе общих факторов (common factor analysis) факторы определяют только на основа-ши общей дисперсии. Общности располагаются на диагонали корреляционной матрицы. Этот летод подходит, если основной задачей является определение латентных переменных и общей исперсии. Этот метод также известен как разложение матрицы (principal axis factoring).

Анализ общих факторов (common factor analysis)

Метод факторного анализа, который оценивает факторы только по общей (для всех факто­ров) дисперсии.

Существуют и другие методы оценки общих факторов. Они включают: метод невзвешенных тименыиих квадратов, обобщенный метод наименьших квадратов, метод максимального гравдоподобия, альфа-факторный метод, распознования образов. Эти методы сложнее, и их не юкомендуется использовать неопытным аналитикам [8].

В табл. 19.3 показано применение анализа главных компонент. В колонке "Исходные" часть таблицы под названием "Общности") видно, что значения общностей для каждой пере­ленной от V_{ до У_в равны 1, поскольку единицы введены в диагональ корреляционной матри-1Ы. Часть табл. 19.3 под названием "Исходные собственные значения" дает собственные значе-ия факторов, которые снижаются при переходе от первого фактора к шестому. Собственное начение фактора указывает полную дисперсию, присущую данному фактору. Полная диспер-ия для всех шести факторов равна 6, т.е. числу переменных. Дисперсия, обусловленная влия-[ием первого фактора, равна 2,731 или 45,52% от полной дисперсии (2,731/6). Аналогично, .исперсия, обусловленная влиянием второго фактора, равна (2,218/6) или 36,97% от полной .исперсии, и два фактора вместе объясняют 82,49% полной дисперсии. Для определения числа )акторов, которые необходимо использовать в анализе, существует несколько методов.

Эпределение числа факторов

Можно вычислить столько главных компонент, сколько имеется переменных, но это не-кономично. Чтобы обобщить информацию, содержащуюся в исходных переменных, лучше ыделить небольшое число факторов. Вопрос в том: сколько? Для определения числа факторов тредлагается несколько процедур: определение, основанное на предварительной информации; пределение, основанное на собственных значениях факторов; критерий "каменистой осыпи"; пределение на основе процента объясненной дисперсии; метод расщепления и критерии начимости.

Определение, основанное на предварительной информации. Иногда, руководствуясь предва-

ительной информацией, исследователь знает, сколько факторов можно ожидать, и таким об-

>азом, может заранее определить число выделяемых факторов. После извлечения желаемого

шсла факторов их выделение прекращают. Большинство компьютерных программ позволяют

юльзователю определить число факторов, значительно упрощая применение этого метода.

Определение, основанное на собственных значениях факторов. В этом методе учитывают только факторы, собственные значения которых выше 1,0; остальные факторы в модель не включают. Собственное значение представляет значение дисперсии, обусловленной действием этого фактора. Следовательно, рассматривают только факторы с дисперсией выше 1,0. Если 1исло переменных меньше 20, то этот метод завышает число факторов.

Определение, основанное на критерии "каменистой осыпи". Графическое изображение кри-герия "каменистой осыпи" представляет собой график зависимости собственных значений факторов от их номеров в порядке выделения. Для определения числа факторов используют форму графика. Обычно график имеет четкий разрыв между крутой частью кривой, где факто­рам свойственны большие собственные значения, и плавной хвостовой частью кривой, связан­ной с остальными факторами (в этом месте убывание собственных значений факторов слева направо максимально замедляется). Это плавное убывание собственных значений называется осыпь (scree). Опыт показывает, что точка, с которой начинается осыпь, указывает на действи­тельное число факторов. Обычно число факторов, определенное по графику "каменистой осы-

пи", на единицу или несколько единиц больше числа факторов, полученных методом, оснс ванным на собственных значениях.

Определение на основе процента объясненной дисперсии. В этом методе число выделяемы факторов определяют так, чтобы кумулятивный процент дисперсии, выделяемой факторамр достиг удовлетворительного уровня. Какой уровень дисперсии считать удовлетворительны!; зависит от поставленной задачи. Однако рекомендуется выделять такое число факторов, коте рое объясняют, по крайней мере, 60% дисперсии.

Определение, основанное на оценке надежности, выполняемой расщеплением. В этом метод выборку расщепляют напополам и факторный анализ выполняют для каждой половины. Пр этом оставляют только факторы с высокой степенью соответствия факторных нагрузок в дву подвыборках.

Определение, основанное на критериях значимости. Можно определить статистическую зна чимость отдельных собственных значений и оставить только статистически значимые факте ры. Недостаток этого метода в том, что при больших размерах выборок (больше 200) многи факторы, вероятно, статистически значимые, хотя с практической точки зрения, многие из ни объясняют небольшую долю полной дисперсии.

В табл. 19.3, исходя из собственных значений факторов, превышающих единицу (по умол чанию), будет выделено два фактора. Из опыта (предварительная информация) мы знаем, чт зубную пасту покупают по двум основным причинам. График "каменистой осыпи" приведе] на рис. 19.2.

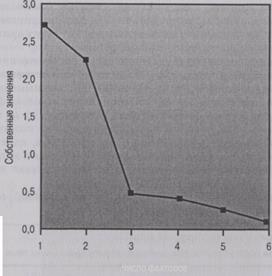
Число факторов Рис. 19.2. График "каменистойосыпи"

На графике четкий разрыв виден в области трех факторов. И наконец, из значения кумуля тивного процента объясненной дисперсии видно, что два первых фактора объясняют 82,49Я дисперсии, и увеличение этого значения при переходе к трем факторам будет предельным Кроме того, метод расщепления выборки также указывает на два фактора. Таким образом, ] данной ситуации целесообразно рассмотреть два фактора.

Во второй колонке части табл. 19.3 под названием "Общности" дана информация после вы деления желаемого числа факторов. Общности в колонке "Выделенная" отличаются от значе ний в колонке "Начальная", поскольку всю дисперсию, соответствующую этим переменным нельзя объяснить, если не оставить в модели все факторы. В части таблицы под названиех "Сумма квадратов нагрузок выделенных факторов" даны дисперсии, соответствующие факто

рам, которые оставили в модели. Обратите внимание, что их значения совпадают со значения­ми дисперсий в колонке "Исходные собственные значения". Это характерно для анализа глав­ных компонент. Процент дисперсии, объясненной фактором, определяют, разделив соответст­вующее собственное значение на число факторов и умножив полученное значение на 100. Та-:им образом, первый фактор объясняет (2,731/6) х 100, или 45,52%, от дисперсии, оответствующей шести переменным. Аналогично, второй фактор объясняет (2,218/6) х 100, или 36,969% полной дисперсии. Интерпретация решения часто становится более ясной после вращения факторов.

Вращение факторов

Важный результат факторного анализа — матрица факторных нагрузок, также называемая матрицей факторного отображения (factor pattern matrix). Она содержит коэффициенты, ис-юльзуемые для выражения нормированных переменных через факторы. Эти коэффициенты, взываемые факторными нагрузками, представляют корреляции между факторами и перемен-

MH. Коэффициент с высоким абсолютным значением показывает, что фактор и переменная тесно взаимосвязаны. Коэффициенты матрицы факторных нагрузок можно использовать для интерпретации факторов.

Несмотря на то, что матрица исходных или неповернутых факторов указывает на взаимо­связь факторов и отдельных переменных, она редко приводит к факторам, которые можно ин­терпретировать, поскольку факторы коррелируют со многими переменными. Например, в габл. 19.3 фактор 1, по крайней мере, частично связан с пятью из шести переменных (абсолютное значение факторной нагрузки больше 0,3). Как интерпретировать этот фактор? В такой сложной матрице это трудно. Поэтому вращением матрицу факторных коэффициентов преобразуют в более простую, которую легче интерпретировать.

При вращении факторов желательно, чтобы каждый фактор имел ненулевые или значи­мые нагрузки (коэффициенты) только для небольшого числа переменных. Аналогично, же­лательно, чтобы каждая переменная имела ненулевые или значимые нагрузки с небольшим числом фактором, если можно, то с одним фактором. Если несколько факторов имеют высо­кие значения факторных нагрузок с одной и той же переменной, то их трудно интерпретиро­вать. Вращение не влияет на общности и процент объясненной полной дисперсии. Однако процент дисперсии, обусловленной влиянием каждого фактора, изменяется. Это видно из данных табл. 19.3. В результате вращения дисперсия, объясняемая каждым фактором, пере­распределилась. Следовательно, разные методы вращения помогают интерпретировать раз­личные факторы.

Вращение называют ортогональным вращением (orthogonal rotation), если при вращении со­храняется прямоугольная система координат.

Ортогональное вращение (orthogonal rotation)

Вращение факторов, при котором сохраняется прямоугольная система координат.

Самый распространенный метод вращения — метод варимакс (вращение, максимизирующее дисперсию) (varimax procedure).

Метод варимакс, или вращение, максимизирующее дисперсию) (varimax procedure)

Ортогональный метод вращения факторов, который минимизирует число переменных с вы­сокими значениями нагрузок, усиливая тем самым интерпретируемость факторов.

Это ортогональный метод вращения, который минимизирует число переменных с высоки­ми значениями нагрузок, усиливая тем самым интерпретируемость факторов [9]. В результате ортогонального вращения получают некоррелированные факторы. Вращение называют косо­угольным вращением (oblique rotation), если не сохраняется прямоугльная система координат и в результате вращения получают коррелированные факторы.

Косоугольное вращение (oblique rotation)

Вращение факторов, при котором не сохраняется прямоугольная система координат.

Иногда, допустив некоторую корреляцию между факторами, можно упростить матриц факторной модели. Косоугольное вращение используется тогда, когда факторы в генерально! совокупности, вероятно, тесно взаимосвязаны.

Сравнив в табл. 19.3 матрицу факторных нагрузок, полученную после применения метод вращения варимакс, с матрицей факторных нагрузок до вращения (часть таблицы под назва нием "Матрица факторных нагрузок"), мы увидим, как вращение упрощает и усиливает ин терпретируемость факторов. В то время как в неповернутой матрице пять переменных коррели руют с фактором 1, после вращения с фактором 1 коррелируют только переменные Pj, F₃, И Остальные переменные V₂, V^ и У₆ коррелируют с фактором 2. Более того, ни одна из перемен ных не коррелирует достаточно сильно с обоими факторами. Повернутая матрица создает осно вудля интерпретации факторов.

Интерпретация факторов

Для интерпретации факторов необходимо определить переменные, которые имеют высоки значения нагрузок по одному и тому же фактору. А затем этот фактор следует проанализировав с учетом этих переменных. Другое полезное средство интерпретации — графическое изображе ние переменных, координатами которых служат величины факторных нагрузок. Так, в конц оси расположены переменные, которые имеют большие нагрузки только в связи с этим факто ром и, следовательно, характеризуют его. Переменные в начале координат имеют небольши нагрузки в связи с обоими факторами. Переменные, расположенные вдали от осей, связаны « обоими факторами. Если фактор нельзя четко определить с точки зрения связи с исходным! переменными, то его следует пометить как неопределяемый или генеральный (общий для все: переменных).

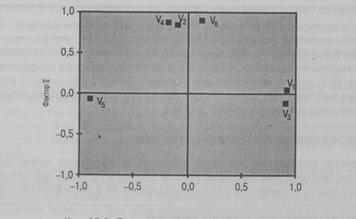
Фактор 1

Рис. 19.3. Диаграмма факторных нагрузок

В повернутой матрице из табл. 19.3 фактор 1 имеет высокие коэффициенты для перемен­ных V_l (предотвращение кариеса), У_ъ (укрепление десен), и отрицательный коэффициент дл* переменной У₅ (предотвращение порчи зубов не считается важным при покупке зубной пасты) Следовательно, этот фактор можно назвать фактором, укрепляющим здоровье. Обратите вни­мание, что отрицательный коэффициент для негативной переменной У₅ ведет к положитель­ной интерпретации этого фактора, а именно, предотвращение порчи зубов будет важным при покупке зубной пасты. Фактор 2 тесно связан с переменными V₂ (белизна зубов), У₄ (свежее дыхание) и К₆ (привлекательность внешнего вида зубов). Таким образом, фактор 2 можно по-

1етить как фактор, отвечающий за внешний вид. Диаграмма факторных нагрузок на рис. 19.3 [одтверждает эту интерпретацию факторов.

Переменные У₁₉ F₃, У₅ (обозначенные на диаграмме 1, 3 и 5 соответственно) находятся на ;онце горизонтальной оси, причем точка, соответствующая К₅, находится на конце, противо-юложном месту расположения точек, соответствующих У_{ и У₃. В то же время переменные У₂, /_{4 и} У₆ (обозначенные на диаграмме 2, 4 и 6 соответственно) расположены на конце вертикаль-юй оси (фактор 2). Можно обобщить данные, сделав вывод, что потребители, по-видимому, тремятся извлечь двойную пользу из зубной пасты: укрепить здоровье и приобрести хороший внешний вид.