Тестирование базового пути
Базовые понятия
Первым будет рассмотрен способ тестирования базового пути, который был разработан в 1976 году Томом Мак-Клером. К главным преимуществам этого способа относятся:
a) возможность получить оценку комплексной сложности программы;
b) возможность определить необходимое количество тестовых вариантов на основании данной оценки.
Для усвоения рассматриваемого способа тестирования следует изложить и пояснить ряд базовых понятий. Написанная программа представляется в виде потокового графа. К особенностям такого графа можно отнести:
a) граф строится отображением управляющей структуры программы;
b) вершины (узлы) графа соответствую линейным участкам программы;
c) граф ориентирован и его дуги отображают поток управления в программе;
d) среди вершин различают операторные вершины и предикатные вершины;
e) предикатные вершины соответствуют простым условиям. Составное условие (условие, содержащее одну или несколько булевых операций) отображается через набор предикатных вершин;
f) замкнутые области на графе, образованные дугами и вершинами, называются регионами. При этом, окружающая граф среда, рассматривается как дополнительный регион.
Согласно данной стратегии тестирования должно быть записано достаточное число тестов, такое, что каждое решение на этих тестах примет значение истина и ложь, по крайней мере, один раз. Иными словами, каждое направление перехода должно быть реализовано хотя бы один раз. Примерами операторов перехода или решений являются операторы while или if.
Цикломатическая сложность
Цикломатическая сложность представляет собой метрику программного обеспечения, которая обеспечивает количественную оценку логической сложности программы. Цикломатическая сложность определяет количество независимых путей в базовом множестве программы, а также определяет верхнюю оценку количества тестов.
Все независимые пути графа образуют базовое множество. К свойствам базового множества относятся:
a) мощность базового множества равна цикломатической сложности потокового графа;
b) в случае выполнения некоторых тестов гарантируется проверка базового множества.
Тестовый вариант - это однократное выполнение каждого оператора и проверка выполнения каждого условия по ветви FALSE и по ветви TRUE.
Существует три способа для вычисления цикломатической сложности:
a) посредством определения количества регионов:  , где
, где  - количество регионов;
- количество регионов;
b) по формуле через количество вершин и дуг:  , где
, где  - количество дуг,
- количество дуг,  - количество вершин;
- количество вершин;
c) по формуле через предикатные узлы:  , где
, где  – количество предикатных узлов.
– количество предикатных узлов.
Алгоритм тестирования методом базового пути
Тестирование данным методом будет рассмотрено на примере процедуры сортировки вставкой. Алгоритм сортировки вставкой в псевдокоде записывается следующим образом:
Insertion_Sort(A)
1 for j 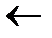 2 to length[A]
2 to length[A]
2 do key 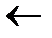 A[j]
A[j]
3 i 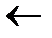 j – 1
j – 1
4 while i > 0 и A[i] > key
5 do A[i + 1] 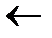 A[i]
A[i]
6 i 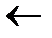 i – 1
i – 1
7 A[i + 1] 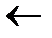 key
key
8 endfor
Шаги тестирования методом базового пути:
Шаг 1. Построение потокового графа на основе выше представленного текста программы. Для начала следует пронумеровать операторы текста, разбив его тем самым на логические блоки.
Изменение нумерации операторов в соответствие с логикой программы:
1 for j 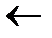 2 to length[A]
2 to length[A]
2 do key 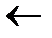 A[j]
A[j]
2 i 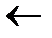 j – 1
j – 1
3 и 4 while i > 0 и A[i] > key
5 do A[i + 1] 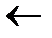 A[i]
A[i]
6 i 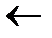 i – 1
i – 1
7 A[i + 1] 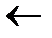 key
key
8 end for
Пусть length[A] ó N.
На построенном графе также обозначаются регионы (рисунок 1).

Рисунок 1 – Потоковый граф процедуры Insertion_Sort
Шаг 2. Определение цикломатической сложности построенного потокового графа. Для этого используются все три вышеописанных способа:
a)  ;
;
b)  ;
;
c)  .
.
Таким образом, цикломатическая сложность потокового графа равна 6.
Шаг 3. Определение базового множества независимых путей, количество которых определяется по цикломатической сложности:
Путь 1: 1-8 // N > 1, массив не отсортирован
Путь 2: 1-2-3-7-8 // N > 1
Путь 3: 1-2-3-4-7-8 // N > 1, массив отсортирован
Путь 4: 1-2-3-4-5-6-7-8 // N = 1
Путь 5: 1-2-3-4-5-6-7-1-8 // N > 3
Путь 6: 1-2-3-4-5-6-3-…-7-8 // N > 1
Шаг 4. Подготовка тестовых вариантов (ТВ):
ТВ 1: Исходные данные: N = 1, A = {5} – массив состоит из одного элемента.
Ожидаемый результат: A = {5}; массив упорядочен.
ТВ 2: Исходные данные: N = 5, A = {5, 10, 1, 18, 6} – не отсортированный массив от 2 до N элементов.
Ожидаемый результат: A = {1, 5, 6, 10, 18}; массив упорядочен.
ТВ 3: Исходные данные: N = 5, A = {5, 10, 1, 18, 6} – проверка условия остановки сдвижки элементов массива (размером от 2 до N) влево (i > 0).
Ожидаемый результат: A = {1, 5, 6, 10, 18}; массив упорядочен.
ТВ 4: Исходные данные: N = 7, A = {1, 2, 3, 5, 6, 9, 29} – отсортированный массив от 2 до N элементов.
Ожидаемый результат: A = {1, 2, 3, 5, 6, 9, 29}; массив упорядочен.
ТВ 5: Исходные данные: N = 5, A = {5, 10, 1, 18, 6} – проверка сдвижки элементов массива (размером от 2 до N) влево (i  i – 1).
i – 1).
Ожидаемый результат: A = {1, 5, 6, 10, 18}; массив упорядочен.
ТВ 6: Исходные данные: N = 4, A = {99, 78, 2, 41} – массив из i, где i  3.
3.
Ожидаемый результат: A = {2, 41, 78, 99}; массив упорядочен.
